Лекция 14

Обобщенные координаты. Обобщенные силы. Уравнения Лагранжа II рода для случая сил, имеющих потенциал

Обобщенные координаты. Обобщенные силы

Перемещения точек несвободной механической системы во многих случаях не могут быть совершенно произвольными. Они ограничены связями, наложенными на систему. Это приводит к тому, что не все координаты точек независимы друг от друга, и положение системы относительно некоторой системы отсчета определяется заданием только независимых координат. Остальные координаты находятся из уравнений связей.

Обобщенными координатами называются независимые величины q_j, заданием которых однозначно определяется положение всех точек механической системы относительно выбранной системы отсчета.

Производные по времени от обобщенных координат называются обобщенными скоростями .

Для голономных систем число обобщенных координат механической системы равно числу степеней свободы этой системы.

Например, положение материальной точки в трехмерном пространстве полностью определяется заданием трех ее декартовых координат x, y и z, которые можно рассматривать как обобщенные координаты. Следовательно, эта точка имеет три степени свободы.

Положение математического маятника в плоскости определяется углом  его отклонения от вертикали. Угол  можно рассматривать как обобщенную координату математического маятника. Так как положение математического маятника определяется одной обобщенной координатой , то математический маятник имеет одну степень свободы.

В общем случае обобщенные координаты могут иметь различный геометрический и физический смысл. Обобщенными координатами могут быть как линейные, так и угловые величины. Роль обобщенных координат могут играть параметры, имеющие смысл площади или объема. Они могут содержать элементы силовых, моментных и других воздействий на систему.

Во многих случаях взаимнооднозначное соответствие между обобщенными координатами и положением точек механической системы может существовать лишь в некоторой окрестности заданного положения системы. В этом случае говорят о локальной параметризации механической системы.

Обобщенные силы. Общее уравнение динамики в обобщенных силах

Рассмотрим механическую систему с голономными двусторонними идеальными связями, состоящую из n точек и имеющую s степеней свободы. Пусть на точки этой системы действуют силы , ,…, . В случае стационарных связей радиус-вектор i-той точки системы является функцией обобщенных координат q₁, q₂,…,q_s: .

Так как обобщенные координаты зависят от времени: q_j=q_j(t), то скорость i-той точки (радиус-вектор является сложной функцией времени):

. (15.1)

Найдем производную от скорости i-той точки системы по обобщенной скорости : . (15.2)

Теперь запишем для рассматриваемой механической системы общее уравнение динамики в форме: .

Подставим в это уравнение (17.1): .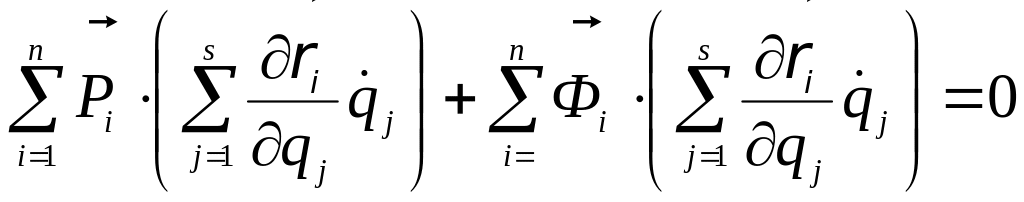

Внесем заданную силу и силу инерции под знаки внутренних сумм, так как они не зависят от индекса j: .

Поменяем местами порядок суммирования и вынесем общий множитель из внутренних сумм: .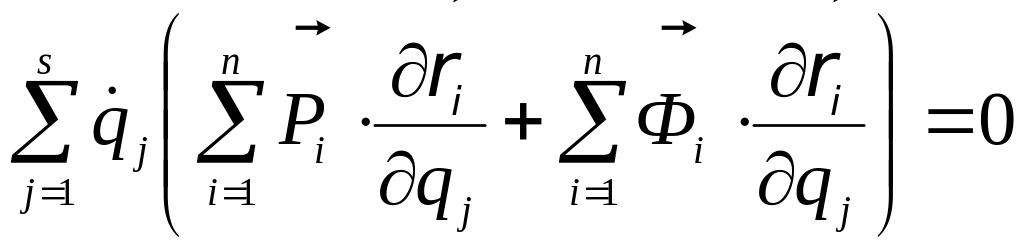

Это уравнение перепишем в виде: . (15.3)

Здесь обозначено

, (15.4)

,

где Q_j– обобщенная задаваемая сила, соответствующая j-той обобщенной координате; – обобщенная сила инерции, соответствующая j-той обобщенной координате.

Если задаваемые силы не зависят от обобщенных скоростей , то есть , то силу в выражении (15.4) можно внести под знак производной:

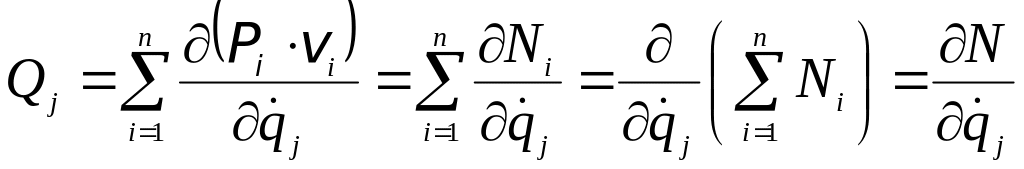, (15.5)

где – мощность i-той силы; .

Суммарная мощность всех сил, действующих на систему:

. (15.6)

Для системы с одной степенью свободы имеем: .

Отсюда . (15.7)

Так как обобщенные скорости могут принимать произвольные значения, то равенство (15.3) может иметь место только при выполнении условия:

(j=1,…,s). (15.8)

Уравнение (15.8) отражает смысл общего уравнения динамики в обобщенных силах: для системы с голономными двусторонними идеальными связями в любой момент времени сумма обобщенной задаваемой силы и обобщенной силы инерции, соответствующих каждой обобщенной координате, равна нулю.