
- •А.В. Индейкин б1.Б.15 «теоретическая механика»
- •23.05.06 «Строительство железных дорог, мостов и транспортных тоннелей»
- •Раздел 1 «статика»
- •Основные понятия теоретической механики
- •Статика. Аксиомы статики. Реакции связей Аксиомы статики
- •Лекция 2
- •Система сходящихся сил
- •2.1. Определение. Сложение сил геометрическим способом. Условие равновесия сил
- •3.2. Проекции силы на ось и на плоскость. Определение равнодействующей аналитическим способом. Уравнения равновесия сил
- •2.3. Теорема о равновесии трех сил
- •Лекция 3 Произвольная система сил в пространстве и на плоскости
- •Система сил, произвольно расположенных в пространстве
- •Лекция 4
- •Лекция 5 Статический расчет плоских ферм
- •Расчет усилий в стержнях фермы
- •7.1. «Способ вырезания узлов»
- •Лекция 6 Трение скольжения и трение качения
- •Сухое трение
- •Лекция 7
- •Центр параллельных сил. Центр тяжести
- •Лекция 8. Рычаг. Устойчивость против опрокидывания.
- •Лекция 9
- •Кинематика. Задачи кинематики. Кинематика точки
- •Лекция 10
- •Лекция 11
- •Лекция 12
- •Лекция 13
- •Определение ускорений точек плоской фигуры
- •Лекция 14
- •Лекция 15
- •Лекция 16
- •Абсолютное, переносное и относительное движения точки
- •Семестр 3
- •Раздел 3 динамика лекция 1
- •Лекция 2 Динамика механической системы
- •Лекция 3 Моменты инерции твердых тел
- •Лекция 4 Динамика механической системы
- •Лекция 5 Количество движения механической точки и механической системы
- •Лекция 6 Динамика вращательного и плоского движения твердого тела
- •Лекция 7
- •Лекция 8
- •Лекция 9
- •Лекция 10
- •Лекция 11 Принцип возможных перемещений
- •Лекция 12 общее уравнение динамики
- •Лекция 13
- •Лекция 14
- •Уравнения Лагранжа II рода
- •Лекция 15
- •Лекция 16 Свободные и вынужденные колебания механической системы с одной степенью свободы.
Лекция 15
Движение свободного твердого тела (Общий случай движения тела)
Движение свободного твердого тела (Общий случай движения тела)
Движение свободного твердого тела в пространстве следует рассматривать как сложное движение – поступательное вместе с полюсом и сферическое – вокруг полюса. В связи с таким подходом запишем уравнения движения свободного твердого тела:
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
П ервые
три уравнения характеризуют поступательную
часть движения тела относительно
неподвижной системы координат
ервые
три уравнения характеризуют поступательную
часть движения тела относительно
неподвижной системы координат
![]() ,
,![]() ,
,![]() ,
а вторые три – сферическую часть движения
относительно полюса
(см.рис.14.1).
,
а вторые три – сферическую часть движения
относительно полюса
(см.рис.14.1).
Рис.14.1
По аналогии с плоским движением тела
(вывод принципиально одинаков) скорость
точки
![]() свободного твердого тела:
свободного твердого тела:
![]() ,
,
где
![]() и
и
![]() (скорость точки
в сферическом движении тела по отношению
к полюсу
);
(скорость точки
в сферическом движении тела по отношению
к полюсу
);
![]() - скорость полюса
.
- скорость полюса
.
Ускорение точки
:
,
где
![]()
и ![]() ,
, ![]() ;
; ![]() - ускорение полюса
.
- ускорение полюса
.
И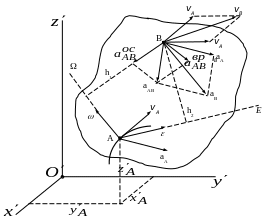 ллюстрации
см. на рис.14.2.
ллюстрации
см. на рис.14.2.
Рис.14.2
Таким образом, получены следующие правила определения скорости и ускорения точек свободного твердого тела.
Скорость любой точки движущегося свободного твердого тела равна геометрической сумме двух скоростей: скорости полюса и скорости этой точки в сферическом движении тела вокруг полюса.
Ускорение любой точки свободного твердого тела (в общем случае его движения) равно геометрической сумме двух ускорений: ускорения полюса и ускорения этой точки в сферическом движении тела вокруг полюса (второе ускорение в свою очередь равно геометрической сумме вращательного и осестремительного ускорений).
Лекция 16
Абсолютное, переносное и относительное движения точки. Теорема о сложении скоростей. Теорема о сложении ускорений.
Абсолютное, переносное и относительное движения точки
Сложным называется такое движение точки, при котором точка одновременно участвует в двух или нескольких движениях. Так, человек, движущийся по эскалатору метрополитена, участвует в двух движениях – вместе с эскалатором и относительно балюстрады эскалатора. Поезд, движущийся по поверхности земли, участвует в двух движениях – вместе с земным шаром по отношению к солнцу и относительно земного шара. В технике существует множество механизмов и различных механических систем, где можно обнаружить сложное движение какого-либо элемента устройства.
Р ассмотрим
движение точки
ассмотрим
движение точки
![]() (рис.15.1) относительно неподвижной системы
отсчета
,
,
,
которое характеризуется радиусом-вектором
(рис.15.1) относительно неподвижной системы
отсчета
,
,
,
которое характеризуется радиусом-вектором
![]() ,
непрерывно изменяющимся с течением
времени:
,
непрерывно изменяющимся с течением
времени:
![]() .
Это движение точки
- результат сложения двух движений.
Рис.15.1
.
Это движение точки
- результат сложения двух движений.
Рис.15.1
Одно из этих движений – движение точки
по отношению к системе отсчета
![]() ,
связанной с движущимся телом
,
связанной с движущимся телом
![]() и поэтому перемещающейся в пространстве
(это движение характеризуется
радиусом-вектором
,
непрерывно изменяющимся с течением
времени
),
и движение точки
вместе с телом
,
движущимся относительно неподвижной
системы отсчета
,
,
.
и поэтому перемещающейся в пространстве
(это движение характеризуется
радиусом-вектором
,
непрерывно изменяющимся с течением
времени
),
и движение точки
вместе с телом
,
движущимся относительно неподвижной
системы отсчета
,
,
.
Первое движение (относительно подвижной системы отсчета) называется относительным, а второе движение точки (вместе с телом ) – переносным. Два этих движения порождают сложное движение точки , которое по отношению к неподвижной системе отсчета называется абсолютным.
Итак, векторное уравнение абсолютного движения: . В этом движении точка обладает абсолютной скоростью и абсолютным ускорением .
Векторное уравнение относительного движения: .
В этом движении точка обладает
относительной скоростью
![]() и абсолютным ускорением
и абсолютным ускорением
![]() .
Переносное движение точки
- это движение точки, как сказано выше,
вместе с телом
,
в этом движении переносной скоростью
точки
.
Переносное движение точки
- это движение точки, как сказано выше,
вместе с телом
,
в этом движении переносной скоростью
точки
![]() становится скорость той точки тела
,
с которой точка
совпадает в данный момент времени. Так
же и переносное ускорение точки
становится скорость той точки тела
,
с которой точка
совпадает в данный момент времени. Так
же и переносное ускорение точки
![]() - это ускорение той точки тела
,
с которой совпадает точка
в данный момент времени. Уравнения
движения тела
позволяют определять скорости и ускорения
точек тела, с которыми совпадает точка
,
участвуя в относительном движении.
- это ускорение той точки тела
,
с которой совпадает точка
в данный момент времени. Уравнения
движения тела
позволяют определять скорости и ускорения
точек тела, с которыми совпадает точка
,
участвуя в относительном движении.
Траекторию точки в переносном движении показать на рисунке невозможно, а вот траектории точки в относительном и абсолютном движениях можно определить и показать, решая конкретную задачу.
Например, если точка движется по образующей прямого кругового конуса , который вращается с угловой скоростью вокруг неподвижной оси , то траектория точки , скорость которой , в относительном движении – прямая линия, совпадающая с образующей конуса. Траектория точки в абсолютном движении (скорость в этом движении ) – винтовая линия, радиус которой непрерывно увеличивается; - переносная скорость точки в данный момент времени (на рис.15.2 показана неподвижная система координатных осей , , и подвижная система координатных осей , связанных с конусом).
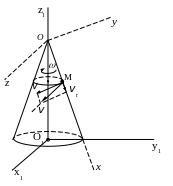
Рис.15.2
Теорема о сложении скоростей
Абсолютная скорость точки в ее сложном
движении равна геометрической сумме
переносной и относительной скоростей:
![]() .
.
Докажем эту теорему, зная переносную и относительную скорости точки (эти скорости определяются по заданным уравнениям переносного движения (движения тела ) и относительного движения).
Так как
![]() (см.рис.15.3), то
(см.рис.15.3), то
![]() , но
, но ![]() ,
,
где
- координаты точки
относительно подвижной системы
![]() ,
связанной с телом
,
поэтому
,
связанной с телом
,
поэтому
![]() . (*)
. (*)
Рассмотрим движение точки
при
![]() ,
тогда
,
тогда
![]()
(получаем скорость точки тела , с которой совпадает точка , не участвующая в относительном движении).
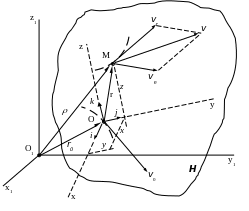
Рис.15.3
Теперь положим
![]() (тело
неподвижно). Получим
(тело
неподвижно). Получим
![]() ,
,
т.е. относительную скорость (переносного
движения нет). Следовательно, в общем
случае
![]() ,
когда происходят одновременно два
движения – переносное и относительное.
,
когда происходят одновременно два
движения – переносное и относительное.
Теорема доказана.
Теорема о сложении ускорений
Абсолютное ускорение точки в ее сложном движении равно геометрической сумме трех ускорений: переносного, относительного и ускорения Кориолиса
![]() .
.
Докажем эту теорему, зная уравнения переносного движения (движения тела ) и уравнения относительного движения точки , которые позволяют определить все три ускорения, а затем и абсолютное ускорение точки .
Так как
![]() ,
то, используя формулу (*), получим:
,
то, используя формулу (*), получим:
![]() .
.
(**)
Если
![]() ,
то
,
то
![]() (точка
не участвует в относительном движении).
(точка
не участвует в относительном движении).
Если
![]() ,
то
,
то
![]() (переносное движение – движение тела
либо отсутствует
(переносное движение – движение тела
либо отсутствует
![]() ,
либо поступательное
,
либо поступательное
![]() ).
).
Замечаем, что и в первом и во втором случаях удвоенная скобка в уравнении (**) исчезает. Однако, в случае двух одновременно происходящих движений:
![]() .
.
Появляется дополнительное ускорение, названное ускорением Кориолиса, в честь открывшего это ускорение французского ученого Кориолиса (это ускорение иногда называют «поворотным» по предложению российского ученого Сомова).
Итак,
,
что и требовалось доказать.
Ускорение Кориолиса определяется
формулой:
![]() ,
что следует из того, что
,
что следует из того, что
![]() ;
;
![]() и
и
![]() ,
,
где
![]() - вектор угловой скорости тела (в
сферическом движении тела – вектор
мгновенной угловой скорости), а
- вектор угловой скорости тела (в
сферическом движении тела – вектор
мгновенной угловой скорости), а
![]() (относительная скорость).
(относительная скорость).
Модуль вектора
![]() определяем формулой
определяем формулой
![]() ,
,
откуда видно, что ускорение Кориолиса
действительно равно нулю при поступательном
переносном движении
![]() ,
а также в тот момент, когда в относительном
движении скорость
,
а также в тот момент, когда в относительном
движении скорость
![]() и когда векторы
и
и когда векторы
и
![]() параллельны.
параллельны.
Н.Е.Жуковский сформулировал правило для определения направления вектора : вектор проектируется на плоскость, перпендикулярную вектору , полученная проекция поворачивается в этой плоскости на угол 900 в направлении, соответствующем направлению угловой скорости - получаем направление вектора ускорения Кориолиса (рис.15.4).
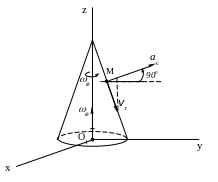
Рис.15.4
Сложное движение тела. Сложение скоростей и ускорений тела при поступательных движениях тела. Сложение угловых скоростей и угловых ускорений составляющих вращений тела вокруг пересекающихся осей
Сложное движение тела
Сложение скоростей и ускорений тела при поступательных движениях тела
Если тело одновременно участвует в двух или нескольких движениях, то в результате получаем сложное движение тела относительно конкретной неподвижной системы отсчета. Если составляющие движения тела – поступательные, то на основании теоремы о сложении скоростей и ускорений абсолютная скорость тела равна геометрической сумме скоростей составляющих движений, а абсолютное ускорение тела равно геометрической суме ускорений составляющих движений (рис.16.1).
![]() ;
; ![]() ,
,
где
![]() - число одновременно происходящих
движений.
- число одновременно происходящих
движений.
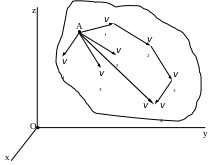
Рис.16.1
Сложное движение тела в этом случае – поступательное, т.к. скорости (и ускорения) точек тела в каждый момент времени геометрически равны.
Сложение угловых скоростей и угловых ускорений составляющих вращений тела вокруг пересекающихся осей
Если тело одновременно участвует в двух
или нескольких вращательных движениях
вокруг осей, пересекающихся в одной
точке, то сложное движение тела
относительно неподвижной системы
отсчета становится сферическим (точка
пересечения осей неподвижна). Мгновенная
угловая скорость тела в этом случае
равна геометрической сумме угловых
скоростей составляющих вращений:
![]() .
.
М гновенное
угловое ускорение:
гновенное
угловое ускорение:
![]() ,
т.е. равно геометрической сумме угловых
ускорений составляющих вращений:
,
т.е. равно геометрической сумме угловых
ускорений составляющих вращений:
![]() .
.
Покажем это на примере двух одновременно происходящих вращений тела вокруг пересекающихся осей (рис.16.2).
Абсолютная скорость точки :
,
Рис.16.2
где
- скорость точки
во вращательном движении тела вокруг
оси
(примем это вращение за переносное
движение),
![]() - скорость точки
во вращательном движении тела вокруг
оси
(примем это вращение за относительное
движение):
- скорость точки
во вращательном движении тела вокруг
оси
(примем это вращение за относительное
движение): ![]() и
и ![]() ,
,
тогда ![]() , где
- мгновенная абсолютная угловая скорость
тела в сложном – сферическом движении
тела.
, где
- мгновенная абсолютная угловая скорость
тела в сложном – сферическом движении
тела.
Таким образом, получаем
![]() и
и ![]() , или
, или ![]()
(мгновенное угловое ускорение тела в сферическом движении).
Сложение угловых скоростей и угловых ускорений составляющих вращений тела вокруг параллельных осей.
Сложение угловых скоростей и угловых ускорений составляющих вращений тела вокруг параллельных осей
Если тело одновременно вращается вокруг двух или нескольких параллельных осей, то по отношению к неподвижной системе отсчета оно совершает плоское движение.
Как известно из теории плоского движения одна из главных характеристик тела в этом случае – абсолютная угловая скорость. Как же определить угловую скорость тела (и угловое ускорение)?
Р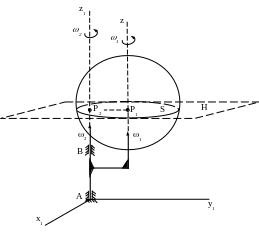 ассмотрим
случай одновременного вращения тела
вокруг двух параллельных осей
и
(см.рис.17.1).
ассмотрим
случай одновременного вращения тела
вокруг двух параллельных осей
и
(см.рис.17.1).
Рис.17.1
Можно представить себе глобус, вращающийся вокруг оси симметрии , которая, в свою очередь, вращается вокруг неподвижной оси подставки .
Таким образом, получим два одновременных
вращения тела вокруг параллельных осей
с угловыми скоростями
![]() и
и
![]() .
Примем вращение тела вокруг оси
за переносное движение, а вращение тела
вокруг оси
за относительное движение.
.
Примем вращение тела вокруг оси
за переносное движение, а вращение тела
вокруг оси
за относительное движение.
Относительная скорость точки
![]() ,
лежащей на оси
,
равна нулю.
,
лежащей на оси
,
равна нулю.
Поэтому можно назвать точку
мгновенным центром скоростей плоской
фигуры
,
связанной с телом, в относительном ее
движении (плоская фигура
получена в результате сечения тела
горизонтальной плоскостью
),
а точка
![]() - мгновенным центром скоростей плоской
фигуры
в ее переносном движении.
- мгновенным центром скоростей плоской
фигуры
в ее переносном движении.
Итак,
![]() и
и ![]() .
.
Д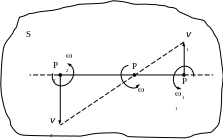 адим
вид сверху на плоскую фигуру
и найдем абсолютные скорости точек
и
,
которые помогут найти мгновенный центр
скоростей плоской фигуры
в ее абсолютном движении (в плоском
движении). Эту операцию проводим согласно
теории плоского движения (см.рис.17.2).
зная, что угловые скорости
адим
вид сверху на плоскую фигуру
и найдем абсолютные скорости точек
и
,
которые помогут найти мгновенный центр
скоростей плоской фигуры
в ее абсолютном движении (в плоском
движении). Эту операцию проводим согласно
теории плоского движения (см.рис.17.2).
зная, что угловые скорости
![]() ,
,
![]() и
и
![]() .
Тогда скорость точки
:
.
Тогда скорость точки
:
![]() ,
а скорость точки
:
,
а скорость точки
:
![]() .
.
Рис.17.2
Показав векторы этих скоростей, находим
мгновенный центр скоростей (точку
![]() )
плоской фигуры
в абсолютном ее движении относительно
неподвижной системы отсчета (в плоском
движении).
)
плоской фигуры
в абсолютном ее движении относительно
неподвижной системы отсчета (в плоском
движении).
Теперь можно найти положение точки -
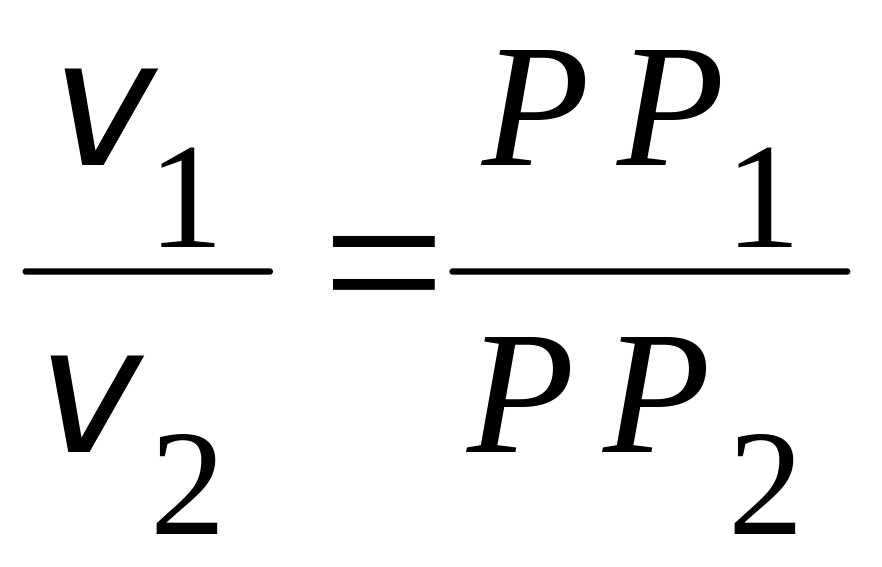 ;
;  ;
; 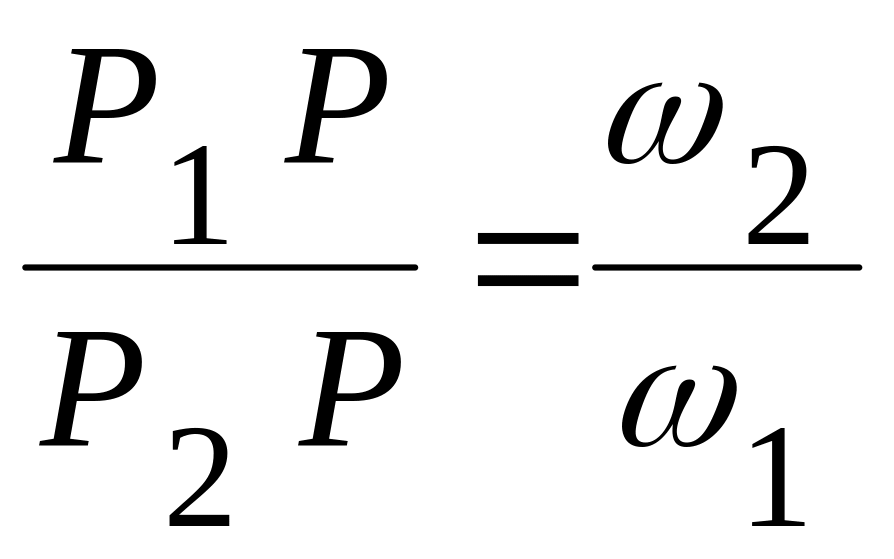 ,
,
т.е. точка
делит отрезок
![]() (расстояние между осями
и
)
на части, обратно пропорциональные
угловым скоростям составляющих вращений.
(расстояние между осями
и
)
на части, обратно пропорциональные
угловым скоростям составляющих вращений.
Теперь находим абсолютную угловую скорость тела :
![]() , откуда
, откуда 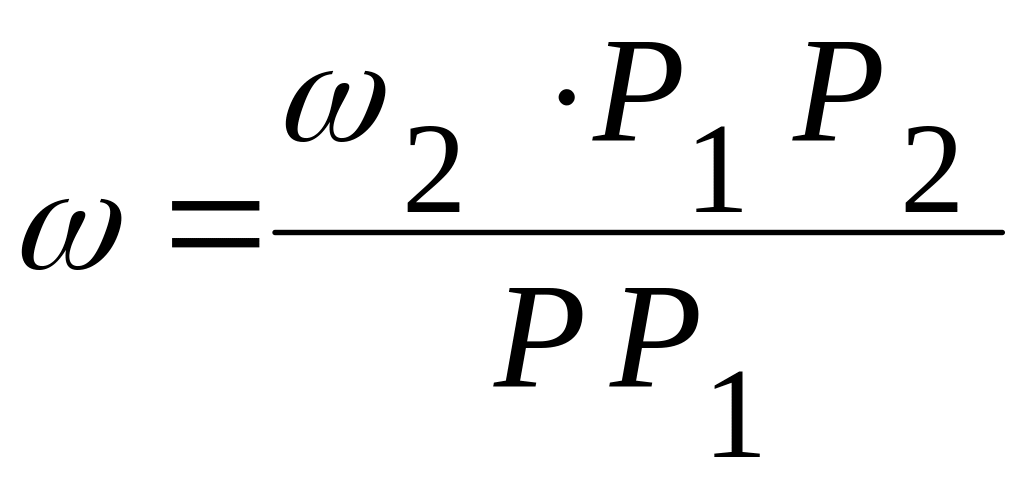 ,
,
но
![]() и
и ![]() ,
,
отсюда
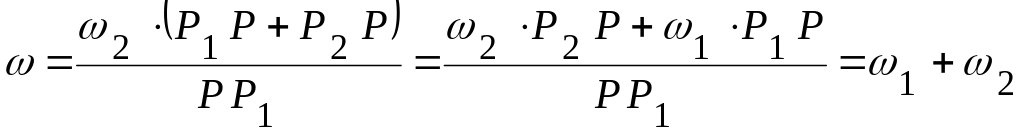
Итак,
![]() .
Вектор
располагается между осями составляющих
вращений на расстояниях от осей, обратно
пропорциональных угловым скоростям.
.
Вектор
располагается между осями составляющих
вращений на расстояниях от осей, обратно
пропорциональных угловым скоростям.
Если угловые скорости составляющих вращений вокруг параллельных осей направлены в одну сторону, то абсолютная угловая скорость тела равна алгебраической сумме заданных угловых скоростей:
![]() .
.
Если угловые скорости составляющих
вращений направлены в противоположные
стороны и не равны (рис.17.3, случай двух
вращений), то картина изменится –
мгновенный центр скоростей находится
за точкой
![]() ,
при этом:
,
при этом:
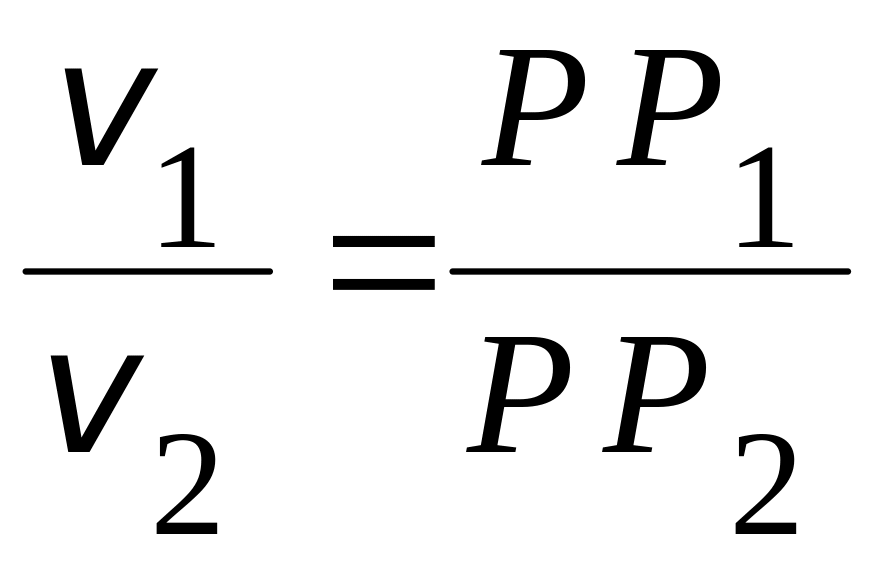 ;
; 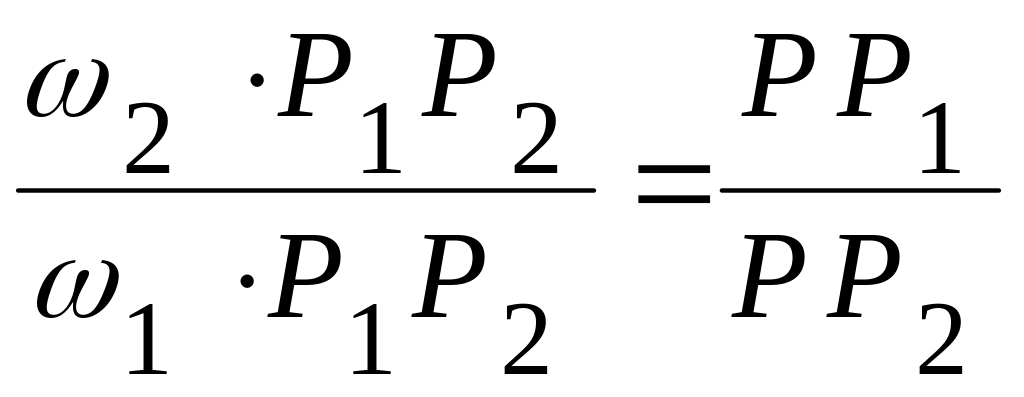 ;
; 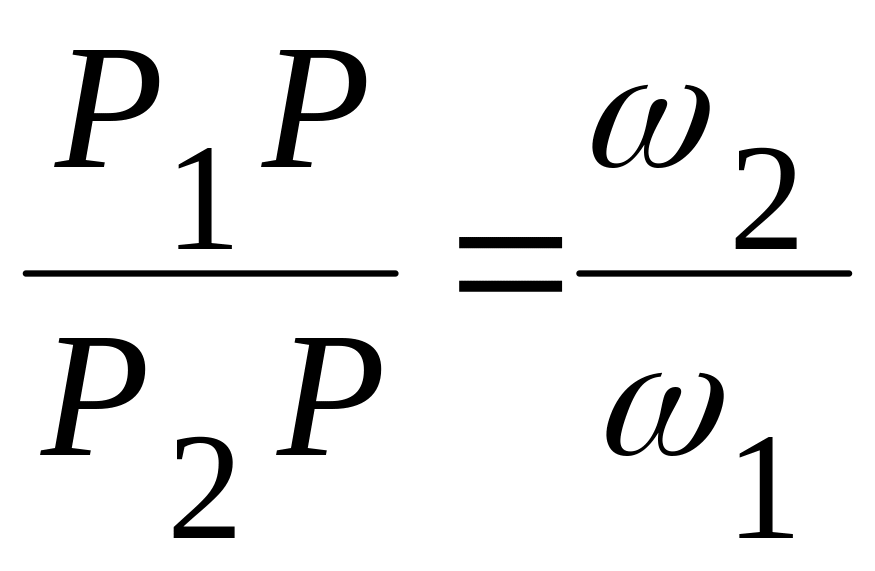 ;
;
![]() , откуда
, откуда  ,
,
но
![]() и
и ![]() ,
,
отсюда
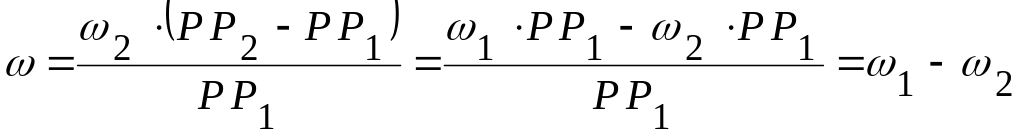 .
.

Рис.17.3
Итак,
![]() .
Вектор
располагается в этом случае за осью,
угловая скорость вокруг которой больше,
на расстояниях от осей составляющих
вращений, обратно пропорциональных
угловым скоростям. Абсолютная угловая
скорость тела равна арифметической
разности заданных угловых скоростей.
.
Вектор
располагается в этом случае за осью,
угловая скорость вокруг которой больше,
на расстояниях от осей составляющих
вращений, обратно пропорциональных
угловым скоростям. Абсолютная угловая
скорость тела равна арифметической
разности заданных угловых скоростей.
Если угловые скорости составляющих вращений вокруг параллельных осей направлены в разные стороны, то абсолютная угловая скорость тела равна арифметической сумме заданных угловых скоростей:
![]()
(угловые скорости одного направления учитываются с одинаковым знаком).
Особый случай:
![]() (угловые скорости двух составляющих
вращений направлены в противоположные
стороны, но равны по величине).
(угловые скорости двух составляющих
вращений направлены в противоположные
стороны, но равны по величине).
С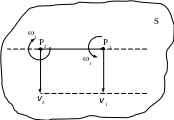 корости
точек
и
(см.рис.17.4), равные по величине, позволяют
утверждать, что в этом случае мгновенный
центр скоростей плоской фигуры
не существует (находится в бесконечности)
и абсолютная угловая скорость тела
равна нулю (в данный момент или в любой
другой момент времени, если
в течение заданного промежутка времени).
корости
точек
и
(см.рис.17.4), равные по величине, позволяют
утверждать, что в этом случае мгновенный
центр скоростей плоской фигуры
не существует (находится в бесконечности)
и абсолютная угловая скорость тела
равна нулю (в данный момент или в любой
другой момент времени, если
в течение заданного промежутка времени).
Рис.17.4
Это означает, что скорости всех точек
тела в любой момент времени геометрически
равны (в заданном интервале времени)
![]() .
.
Ускорения этих точек тела так же геометрически равны:
![]() .
.
Тело, следовательно, (относительно неподвижной системы отсчета) совершает поступательное движение (результат двух одновременных вращений вокруг параллельных осей, когда угловые скорости составляющих вращений равны по величине, но направлены в противоположные стороны).
В этом случае скорость любой точки тела
можно рассматривать как момент пары
угловых скоростей (пары вращений). На
рис.17.5 показана пара угловых скоростей
![]() и момент пары вращений -
(по аналогии с парой сил и ее моментом
в статике).
и момент пары вращений -
(по аналогии с парой сил и ее моментом
в статике).
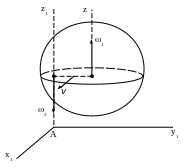
Рис.17.5
