Определение ускорений точек плоской фигуры
Для определения ускорений точек плоской фигуры используется теорема об ускорениях точек: ускорения любой точки плоской фигуры равно геометрической сумме двух ускорений: ускорения полюса и ускорения этой точки во вращательном движении плоской фигуры вокруг полюса.
Приведем доказательство этой теоремы
;
,
но
(по формуле Эйлера), поэтому
,
следовательно,
.
Окончательно,
, т.е. 
,
т.к. 
(рис.12.1).
Теорема доказана.
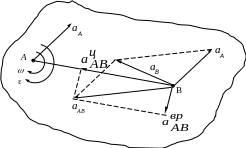
Рис.12.1
У этой теоремы есть два следствия.
П
ервое
следствие: проекция ускорения точки
В на ось, проходящую через отрезок
АВ, всегда меньше, (в крайнем случае
равна) проекции ускорения полюса –
точки А на эту же ось (рис.12.2).
Рис.12.2
Из рисунка видно, что равенство проекций
возможно только в момент, когда
,
а
.
Второе следствие: концы векторов
ускорений точек А, В и С
одного и того же отрезка лежат на одной
прямой и делят отрезок ab
этой прямой на части ас и bc,
пропорциональные отрезкам АС и ВС
на исходном отрезке АВ (рис.12.2). Это
утверждение справедливо потому, что
ускорение точек
и
пропорциональны расстояниям от точек
В и С до полюса А.
Ускорение любой точки плоской фигуры
можно определять с помощью мгновенного
центра ускорений – точки плоской
фигуры, ускорение которой в данный
момент времени равно нулю. В этом случае,
если известны угловая скорость и угловое
ускорение плоской фигуры, ускорение
произвольно выбранной точки В:
,
если
(точка Q – мгновенный
центр ускорений), то
.
Т.е. ускорение точки В равно
геометрической сумме центростремительного
и вращательного ускорений точки во
вращательном движении плоской фигуры
вокруг мгновенного центра ускорений.
На рис.12.3 показаны эти ускорения, при
этом
(
- угол между ускорением
и отрезком BQ, этот
угол отложен от ускорения
в направлении углового ускорения
(см. круговую стрелку
).
Т
олько
в этом случае
(по теореме об ускорениях точек плоской
фигуры) и
,
что дает
(точка Q действительно
мгновенный центр ускорений в данный
момент времени, для которого
и
имеют конкретные числовые значения).
Так как
,
,
то можно утверждать, что ускорения точек
плоской фигуры пропорциональны
расстояниям от этих точек до мгновенного
центра ускорений.
Рис.12.3
Р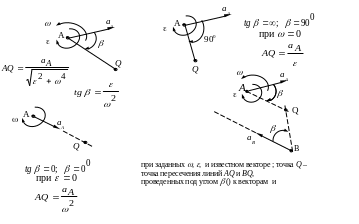
азличные
варианты положения мгновенного центра
ускорений показаны на рис.12.4.
Рис.12.4
Лекция 14
Сферическое движение тела
Сферическое движение тела
Сферическим называется движение тела, у которого одна точка неподвижна. В этом случае любая точка тела, кроме неподвижной, при движении остается на поверхности сферы, радиус которой равен расстоянию от этой точки до неподвижной точки.
П
оложение
тела с одной неподвижной точкой
относительно неподвижных прямоугольных
координатных осей
,
и
(см.рис.13.1) определяется с помощью углов
Эйлера:
- угол нутации (откладывается от оси
в сторону оси
(прямоугольные оси
,
,
жестко связаны с телом и непрерывно
движутся вместе с ним),
- угол прецессии (откладывается от оси
в сторону линии узлов
,
которая получается в результате
пересечения наклонной плоскости
,
с горизонтальной плоскостью
,
),
- угол собственного вращения (откладывается
от линии узлов
в сторону оси
).
Рис.13.1
Нутация – кивание (ось
то приближается к оси
,
то удаляется от нее), прецессия –
предшествование (название взято из
астрономии, день весеннего или осеннего
равноденствия каждый год наступает
чуть раньше, чем в прошлом году, для нас
практически это незаметно и неощутимо),
собственное вращение – вращение
тела вокруг его оси симметрии
,
которая перпендикулярна к плоскости
угла
.
При движении тела все три угла изменяются с течением времени, таким образом, получаем три уравнения сферического движения:
, 
, 
.
Если из трех углов изменяется только
угол
,
то тело вращается вокруг неподвижной
оси – вокруг линии
.
Угловая скорость этого вращения
,
вектор
направляется по линии узлов (см.рис.13.1
при
).
Если из трех углов изменяется только
угол
,
то тело вращается вокруг неподвижной
оси – вокруг линии
.
Угловая скорость этого вращения
,
вектор
направляется по оси
(на рис.13.1 при
).
Если из трех углов изменяется только
угол
,
то тело вращается вокруг неподвижной
оси – вокруг линии
и угловая скорость этого вращения
.
Вектор
направляется по оси
(на рис.13.1 при
).
Если одновременно изменяются все три угла, то тело совершает сферическое движение, которое характеризуется мгновенной угловой скоростью и мгновенным угловым ускорением .
Мгновенная угловая скорость тела
(изображается замыкающей стороной
векторного многоугольника угловых
скоростей – см.рис.13.1). Вектор
определяет положение мгновенной оси
вращения (мгновенной оси угловой
скорости)
.
Так как вектор
непрерывно изменяется с течением
времени, то и положение мгновенной оси
вращения непрерывно изменяется.
Мгновенное угловое ускорение тела можно
найти, используя формулу
.
Построив годограф вектора
,
можно определить мгновенную скорость
конца вектора
-
,
отсюда
,
что позволяет показать вектор
и определить положение мгновенной оси
углового ускорения
(рис.13.1). Мгновенные оси
и
не совпадают, так как векторы
и
не лежат на одной прямой.
Мгновенную ось вращения можно определить как геометрическое место точек тела, скорости которых в данный момент времени равны нулю.
Мгновенную ось углового ускорения можно определить как геометрическое место точек тела, вращательное ускорение которых в данный момент времени равны нулю.
С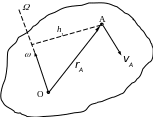
корости
точки тела в его сферическом движении
можно определить, пользуясь формулой
Эйлера, -
(см.рис.13.2), что дает
,
где
- кратчайшее расстояние от точки
до мгновенной оси вращения.
Рис.13.2
Ускорение точки А определяем по формуле
,
т.е.
,
где вращательное ускорение
(
- кратчайшее расстояние от точки
до мгновенной оси углового ускорения),
,
- осестремительное ускорение точки
(см.рис.13.3).
Рис.13.3
Т
ак
как
(в общем случае), то величину ускорения
точки
надо определять, используя тригонометрическую
теорему косинусов (в общем случае векторы
и
не лежат на одной прямой).