Лекция 2

Система сходящихся сил. Сложение сил геометрическим способом. Условие равновесия сил . Проекции силы на ось и на плоскость. Определение равнодействующей аналитическим способом. Уравнения равновесия сил. Теорема о равновесии трех сил

Система сходящихся сил

2.1. Определение. Сложение сил геометрическим способом. Условие равновесия сил

С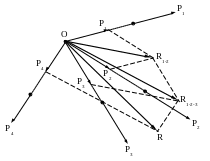 илы, приложенные к телу, линии действия которых пересекаются в одной точке, образуют систему сходящихся сил (рис2.1).

Рис.2.1

Приложим заданные силы к точке О. Для сложения сил используем параллелограмм сил. Силы и дают равнодействующую . Эту равнодействующую складываем с силой , построив еще один параллелограмм, получим равнодействующую сил и , т.е. равнодействующую трех сил . И так далее. Рассматривая картину построений, приходим к выводу, что можно получить результат сложения всех заданных сил построением силового многоугольника, откладывая силы друг за другом, как показано на рис.2.2. Замыкающая сторона векторного (силового) многоугольника (он в общем случае не лежит в одной плоскости) определяет равнодействующую – одну силу, эквивалентную заданной системе сил (надо обратить внимание на «правило стрелок»: обходя многоугольник по контуру, замечаем, что равнодействующая направлена противоположно направлению обхода).

Рис2.2

В результате сложения сил получается одна сила – равнодействующая, равная геометрической сумме сил: .

Если силовой многоугольник замкнут (вектор последней силы заканчивается в точке, где начинается вектор первой силы (см.рис.1.2), то равнодействующая не существует, и сходящиеся силы взаимно уравновешиваются. Условие равновесия сходящихся сил: .

3.2. Проекции силы на ось и на плоскость. Определение равнодействующей аналитическим способом. Уравнения равновесия сил

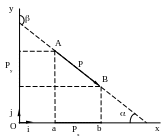
Проекция силы на ось, имеющую заданное ей направление (с помощью единичного вектора-орта), определяется построением, приведенным на рис.2.3. Из точек А и В на ось Оx опускаются перпендикуляры, определяющие отрезок ab лежащий на оси.

Рис.3.3

Длина этого отрезка равна проекции силы на ось Ox - , так же определяется проекция силы на ось Oy - . Получаем , где - угол между вектором и осью Ox; . Но (острого угла) > 0, следовательно , а < 0, следовательно .

Проекция силы на ось – это скалярная величина, она может быть положительной, отрицательной и равной нулю.

П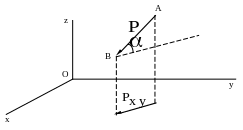 роекция силы на плоскость (рис.2.4, см.также рис.1.1) – вектор, величина и направление которого определяются опусканием перпендикуляров из точек А и В на плоскость xOy: - (модуль вектора ).

Рис.2.4

Зная проекции сходящихся сил, приложенных к телу, можно определить равнодействующую сил аналитическим способом (без построения силового многоугольника). Как видно из рис.2.2 проекции равнодействующей на оси Ox и Oy равны алгебраическим суммам проекций заданных сил на эти же оси: и .

Отсюда следует, что модуль вектора R можно найти по формуле

.

Аналогично, в случае сходящихся сил, не лежащих в одной плоскости, - , или (имеются в виду прямоугольные координатные оси x, y, z).

Направление вектора в пространстве определяют направляющие косинусы углов, которые составляет с осями координат, - ; ; .

Теперь можно записать условия равновесия сил в аналитической форме: уравнения равновесия сходящихся сил. Так как при равновесии сил , то ; ; .

Если силы лежат в одной плоскости, то для решения задач используются два уравнения равновесия, а если силы, приложенные к телу, лежат на одной прямой, то достаточно одного уравнения равновесия.