Лекция 10
Способы задания движения точки
Координатный способ
Определение скорости и ускорения точки
при задании ее движения в декартовых
координатах производится по формулам,
получаемым при рассмотрении векторного
уравнения движения точки
,
где
(
и
- орты координатных осей, а
и
- координаты точки М) (рис.5).
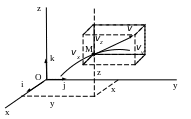
Рис..5
Если заданы уравнения движения точки , и , то
,
отсюда получаем проекции скорости
на оси координат:
;
,
,
что позволяет найти величину скорости
и направление скорости
,
,
,
(направляющие косинусы углов, которые
вектор
составляет с осями координат, их
направления задают орты
,
и
;
обозначение производной по времени в
виде точки над дифференцируемой функцией
введено Ньютоном).
Ускорение точки определяется аналогичным образом:
, откуда 
и
, 
, 
.
Естественный способ
П
ри
естественном способе задания движения
точки вводятся естественные оси
(касательная Т, главная нормаль N
и бинормаль В) – оси подвижной
прямоугольной системы координат с
началом, совпадающим с движущейся точкой
М (рис.6).
Рис.10.6
Касательная (с единичным вектором
)
направлена по касательной к заданной
траектории в положительном направлении
отсчета дуговой координаты S.
Главная нормаль (с ортом
)
направляется перпендикулярно к
касательной в сторону центра кривизны
траектории (проходит через этот центр),
а бинормаль (с ортом
)
перпендикулярна к касательной и главной
нормали и направляется так, чтобы орты
,
и
образовывали правую систему координат.
Через касательную и главную нормаль
проходит соприкасающаяся плоскость F,
через главную нормаль и бинормаль
проходит нормальная плоскость Q,
а через касательную и бинормаль проходит
спрямляющая плоскость P.
Эти три плоскости образуют естественный
трехгранник, который перемещается в
пространстве вместе с точкой М как одно
целое твердое тело (его движение
определяется заданной траекторией и
заданным уравнением движения
).
Скорость точки определяем следующим образом:
,
где
(из дифференциальной геометрии), а
- проекция скорости
на касательную. Итак,
,
а
- модуль вектора
.
Знак производной
определяет направление вектора
.
Ускорение точки 
.
Определяем
,
где
- вектор кривизны траектории,
- радиус кривизны траектории в данной
точке.
Теперь получим 
, где
- нормальное ускорение,
- касательное ускорение,
- проекция ускорения точки М на
касательную; знак этой производной
определяет направление касательного
ускорения.
Так как 
, 
.
Нормальное ускорение точки, направленное по главной нормали к центру кривизны траектории, характеризует изменение направления скорости , а касательное ускорение – изменение величины скорости.
Вектор
всегда лежит в соприкасающейся плоскости,
поэтому проекция ускорения
на бинормаль равна нулю. Если знаки
и
совпадают, то движение точки считается
ускоренным, в противном случае –
замедленным.
Если
, а 
(в течение заданного промежутка времени),
то движение точки называется равномерным
(величина скорости постоянна).
Если
(в течение заданного промежутка времени),
то движение точки называется равнопеременным
(равноускоренным, если
и
одного знака и равнозамедленным,
если
и
разных знаков).
Уравнение равномерного движения точки
по любой траектории:
,
где
- значение дуговой координаты при
.
Уравнение равнопеременного движения
точки по любой траектории:
,
где
и
- значения дуговой координаты и скорости
точки при
(эти уравнения известны еще из школьного
курса физики).
Из последнего уравнения можно получить уравнение, характеризующее изменение величины скорости точки при равнопеременном ее движении:
, или 
(величина касательного ускорения берется с плюсом при равноускоренном движении и с минусом – при равнозамедленном движении).