Лекция 9

Теорема об изменении кинетической энергии материальной точки. Теорема об изменении кинетической энергии механической системы. Случай абсолютно твердого тела.

Теорема об изменении кинетической энергии материальной точки

Найдем связь между изменением кинетической энергии материальной точки и работой сил, действующих на нее. Запишем основное уравнение динамики и умножим обе части этого уравнения скалярно на вектор скорости точки:

.

Так как , где − сумма мощностей сил, приложенных к точке, а , то это выражение приобретает вид:

. (10.1)

Производная по времени от кинетической энергии материальной точки равна мощности сил, действующих на нее.

Умножим обе части равенства (10.1) на dt

и проинтегрируем в пределах, соответствующих начальному и конечному положениям точки М .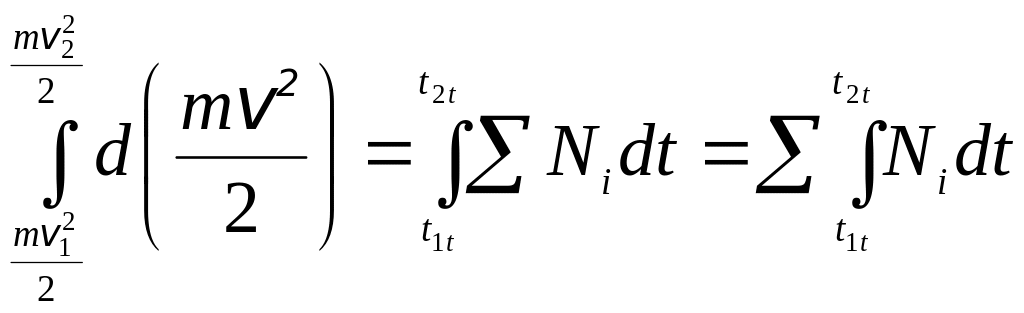

Отсюда . (10.2)

Выражение (10.2) отражает смысл теоремы об изменении кинетической энергии материальной точки: изменение кинетической энергии материальной точки на некотором перемещении равно алгебраической сумме работ сил, действующих на нее, на том же перемещении.

Теорема об изменении кинетической энергии механической системы. Случай абсолютно твердого тела

Выявим зависимость между изменением кинетической энергии механической системы и работой сил, действующих на нее. Для этого рассмотрим i-тую точку М_i механической системы массы m_i, к которой приложены равнодействующая внешних и внутренних сил (рис. 10.1).

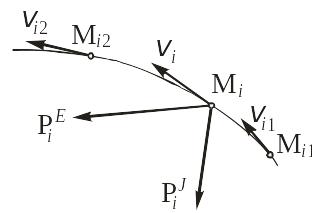
Рис. 10.1

Рассмотрим два момента времени: начальный t₁ и конечный t₂.

Пусть в эти моменты точка имела скорости и , соответственно. Для каждой точки механической системы запишем теорему об изменении кинетической энергии (10.2): , (i=1,2,…,n), где n − количество точек системы, , − работы внешней и внутренней сил.

Складывая почленно все эти равенства, имеем:

.

Учитывая выражение для кинетической энергии механической системы, получаем:

. (10.3)

Это выражение представляет собой математическую запись теоремы об изменении кинетической энергии механической системы: изменение кинетической энергии механической системы на некотором перемещении ее точек равно алгебраической сумме работ внешних и внутренних сил, приложенных к материальным точкам системы, на том же перемещении.

Как было установлено выше, сумма работ всех внутренних сил, действующих на точки твердого тела, равна нулю: =0. Поэтому для твердого тела выражение (10.3) упрощается: . (10.4)

Изменение кинетической энергии твердого тела на некотором перемещении равно алгебраической сумме работ внешних сил, приложенных к точкам тела, на том же перемещении.

Лекция 10

Принцип Германа-Эйлера-Даламбера для материальной точки. Определение главного вектора и главного момента сил инерции точек твердого тела. Определение динамических реакций опор твердого тела, вращающегося вокруг неподвижной оси.

Принцип Германа-Эйлера-Даламбера для материальной точки

При решении задач динамики несвободной материальной точки часто бывает удобно применять так называемый метод кинетостатики (принцип Германа-Эйлера-Даламбера). Суть этого метода состоит в следующем.

Рассмотрим материальную точку М массы m, движущуюся под действием некоторой системы сил , ,…, (среди этих сил могут быть как задаваемые силы, так и реакции связей) с ускорением (рис. 11.1).

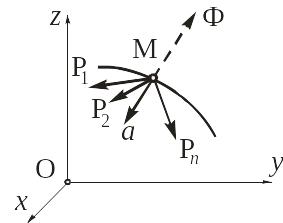
Рис. 11.1

Для этой точки запишем основное уравнение динамики:

.

Перепишем это уравнение в виде и введем обозначение .

В результате получим: . (11.1)

Вектор , равный по модулю произведению массы точки на модуль ее ускорения и направленный противоположно ускорению точки, называется силой инерции.

На основании уравнения (11.1) можно утверждать, что при движении материальной точки в любой момент времени геометрическая сумма сил, действующих на нее, и силы инерции равна нулю.

Метод кинетостатики является формальным приемом, позволяющим записать уравнения динамики в виде уравнений равновесия, применяемых в статике.

При решении практических задач следует помимо действующих на материальную точку заданных сил и реакций связей условно приложить к ней силу инерции. Тогда суммы проекций сил , ,…, , на оси координат будут равны нулю.

Следует иметь в виду, что к материальной точке приложены только силы , ,…, , то есть задаваемые силы и реакции связи. Сила же инерции к точке не приложена. Она приложена к телу, сообщающему материальной точке ускорение.

Метод кинетостатики в ряде случаев позволяет упростить составление уравнений движения в динамике и получить удобное решение задач динамики точки.

Принцип Германа-Эйлера-Даламбера для механической системы

Рассмотрим несвободную механическую систему, состоящую из n материальных точек М₁, М₂,…, М_n. Пусть к i−той точке М_i этой системы приложены − равнодействующая задаваемых сил и − равнодействующая реакций связей. Согласно принципу Германа-Эйлера-Даламбера для материальной точки:

(i=1, 2,…, n), (11.2)

где , , − сила инерции, масса и ускорение материальной точки М_i.

Уравнение (11.2) выражает смысл принципа Германа-Эйлера-Даламбера для несвободной механической системы: при движении механической системы в любой момент времени геометрическая сумма равнодействующих задаваемых сил, реакций связей и силы инерции для каждой материальной точки несвободной механической системы равна нулю.

Складывая почленно все уравнения (11.2), получаем: .

Первая сумма равна главному вектору всех задаваемых сил, действующих на систему. Вторая сумма равна главному вектору всех реакций связей, а третья − главному вектору сил инерции всех материальных точек системы.

С учетом этого можно записать . (11.3)

Это уравнение свидетельствует о том, что в каждый момент времени геометрическая сумма главных векторов задаваемых сил, реакций связей и сил инерции материальных точек несвободной механической системы равна нулю.

Выберем произвольный полюс О, проведем из него в каждую точку М_i системы радиус-вектор и умножим слева каждое из уравнений (11.2) векторно на этот радиус-вектор: (i=1, 2,…, n).

Суммируя почленно эти уравнения, получаем:

.

В этом выражении первая сумма представляет собой главный момент задаваемых сил относительно центра О, вторая сумма − главный момент реакций связей относительно центра О, а третья − главный момент сил инерции относительно центра О.

Таким образом: + + =0. (11.4)

Выражение (13.4) показывает, что в каждый момент времени геометрическая сумма главных моментов задаваемых сил, реакций связей и сил инерции точек несвободной механической системы относительно произвольного неподвижного центра равна нулю.

Двум векторным уравнениям (11.3) и (11.4) соответствуют шесть уравнений в проекциях на оси координат:

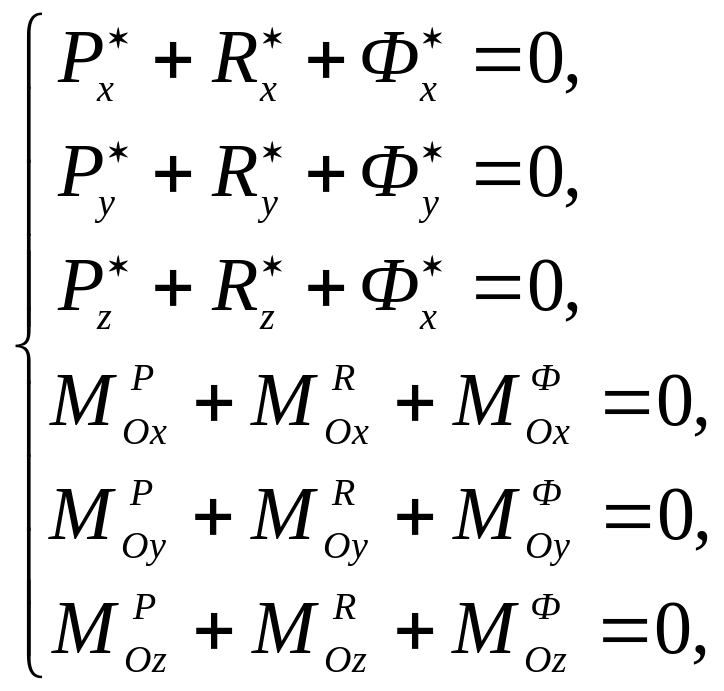. (11.5)

Движение одного твердого тела полностью определяется этими уравнениями. Если же рассматривается движение системы твердых тел, то следует составить подобные уравнения для каждого из тел в отдельности.

Применение принципа Германа-Эйлера-Даламбера при решении задач о движении твердого тела во многом связано с необходимостью определять главный вектор и главный момент его сил инерции.

Определение главного вектора и главного момента сил инерции точек твердого тела

Главный вектор сил инерции точек твердого тела может быть найден обычным путем как геометрическая сумма сил инерции всех точек этого тела:

, (11.6)

где − ускорение центра масс С тела, m − его масса.

Главный вектор сил инерции точек твердого тела по модулю равен произведению массы тела на модуль ускорения центра масс и направлен в сторону, противоположную ускорению его центра масс.

Жестко свяжем с телом систему координат Оxyz и спроецируем векторное уравнение (13.6) на оси этой системы. Тогда проекции главного вектора сил инерции на оси Оx, Оy и Оz:

, , , (11.7)

где , , − проекции ускорения центра масс С тела на оси координат.

Рассмотрим случай, когда точка О, являющаяся началом системы координат Оxyz, неподвижна, и перейдем к определению главного момента сил инерции твердого тела относительно этой точки:

. (11.8)

Найдем производную по времени от кинетического момента твердого тела относительно центра О :

. (11.9)

Сравнивая (11.8) и (11.9), получаем:

. (11.10)

Из курса кинематики известно, что если некоторый вектор задан в подвижной системе координат, то абсолютная производная по времени от этого вектора определяется формулой: , (11.11)

где − относительная производная вектора , − угловая скорость подвижной системы координат по отношению к неподвижной, , , − проекции вектора на оси подвижной системы координат.

Примем за полюс центр масс С тела и перепишем выражение (11.10), используя соотношение (11.11): .

Кинетический момент тела можно записать в матричной форме: ,

где 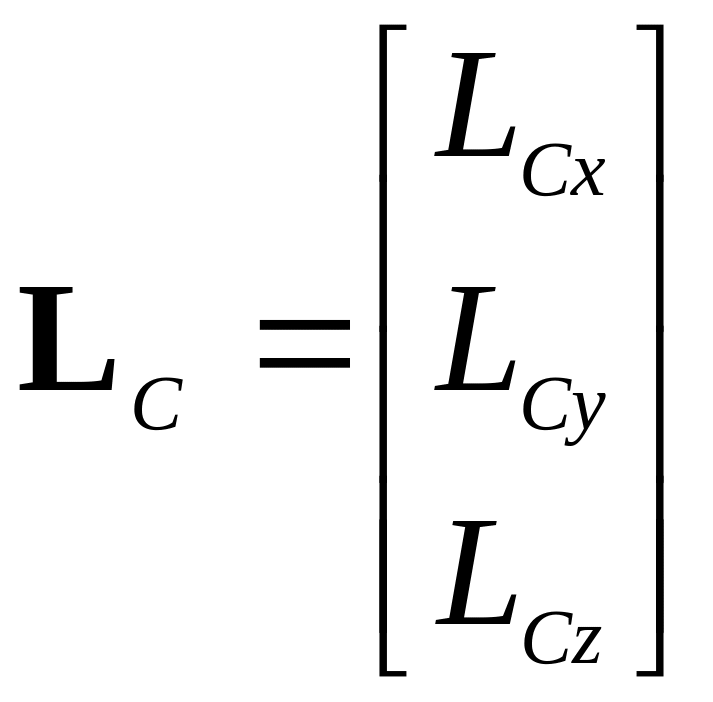− матрица кинетического момента твердого тела;

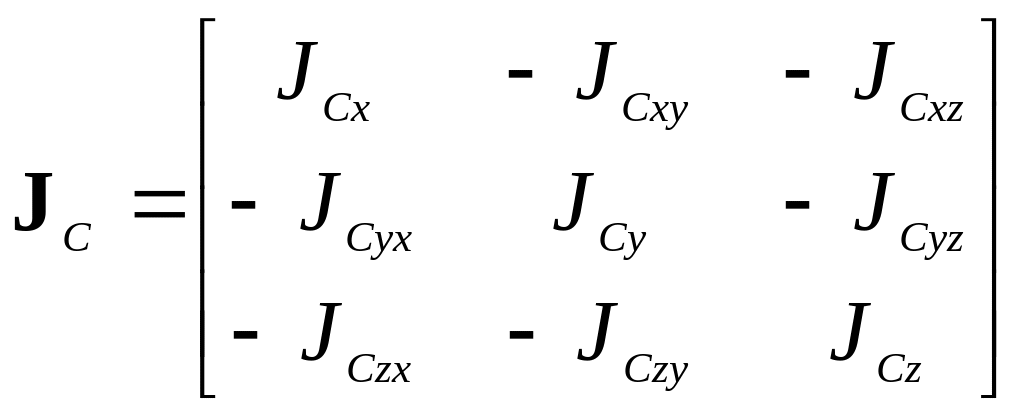− тензор инерции тела относительно центра масс; − матрица угловой скорости тела.

Отсюда ,

где 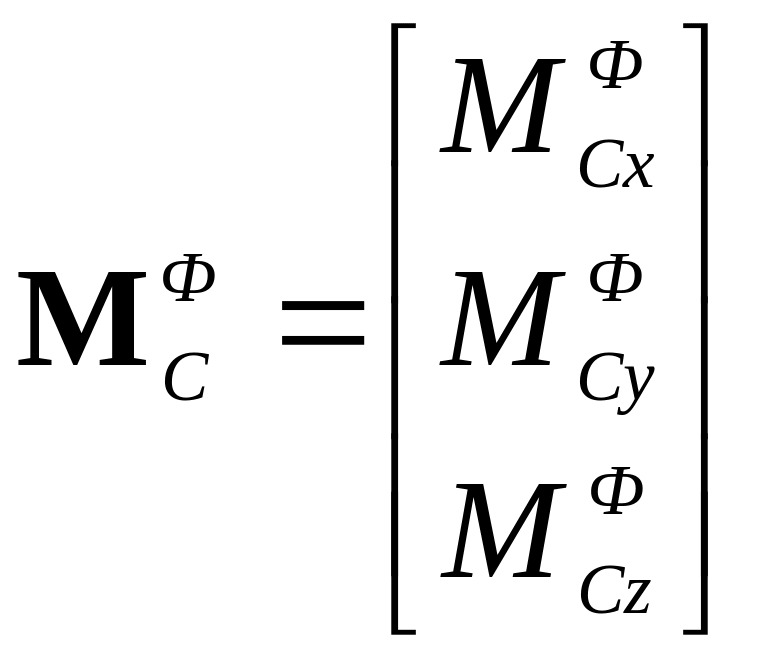− матрица кинетического момента тела относительно центра масс; – кососимметричная матрица угловой скорости тела.

Пусть система координат Cxyz жестко связана с телом, тогда его тензор инерции по отношению к этой системе с течением времени не изменяется. Следовательно ,

где 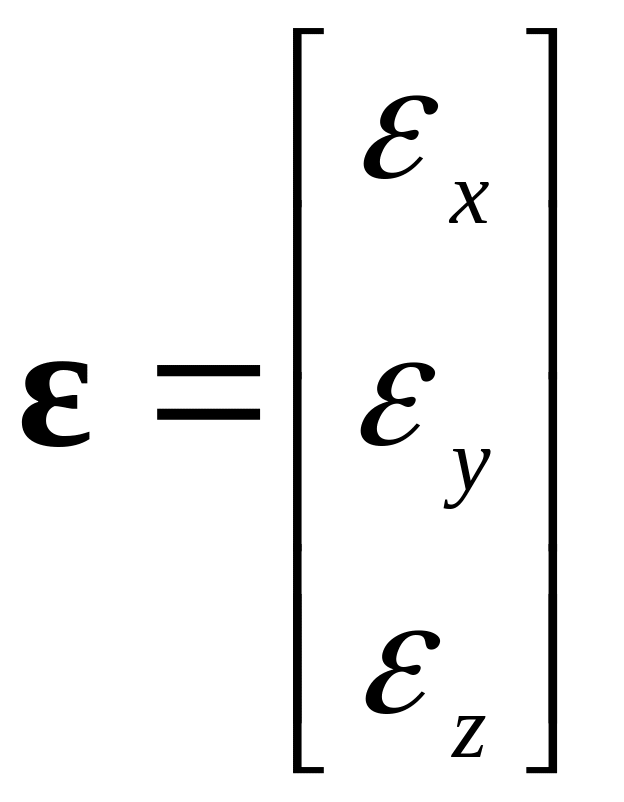− матрица углового ускорения тела.

С учетом этого получаем: .

В развернутой форме:

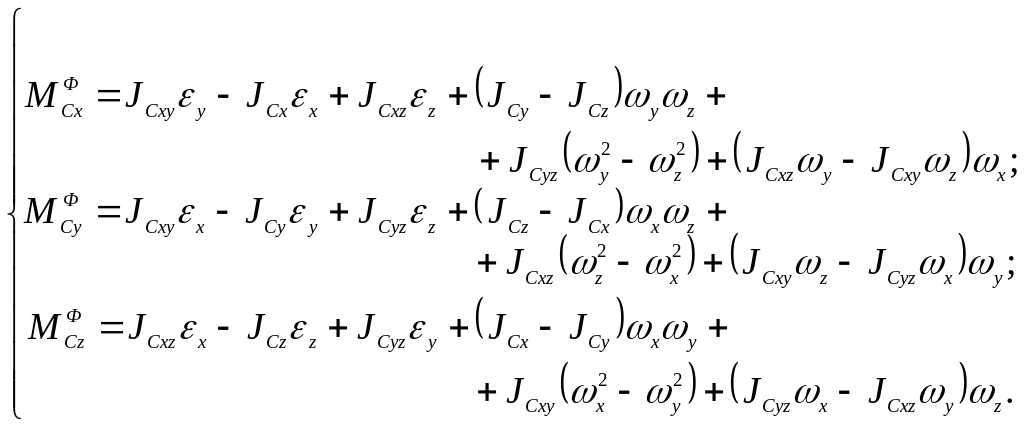(11.12)

Формулы (11.7) позволяют определить проекции главного вектора сил инерции точек свободного твердого тела на оси подвижной системы координат, связанной с телом, а формулы (11.12) − проекции главного момента сил инерции на оси подвижной системы координат Сxyz.

Рассмотрим некоторые частные случаи.

1. Поступательное движение. При поступательном движении угловая скорость и угловое ускорение твердого тела равны нулю, это возможно, если проекции векторов и 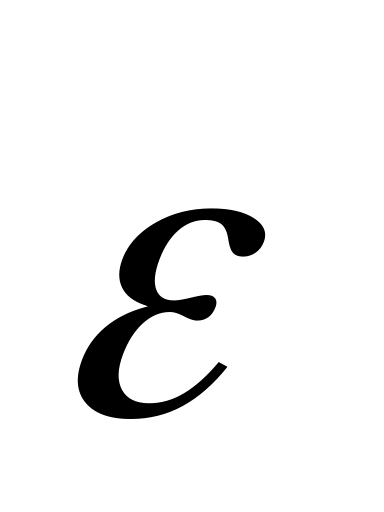на оси произвольно выбранной системы координат равны нулю (_x=_y=_z=0 и _x=_y=_z=0). Из формул (11.12) вытекает, что в этом случае главный момент сил инерции обращается в ноль. Следовательно, при поступательном движении силы инерции точек твердого тела приводятся к равнодействующей, приложенной к центру масс тела и равной главному вектору сил инерции (11.6): .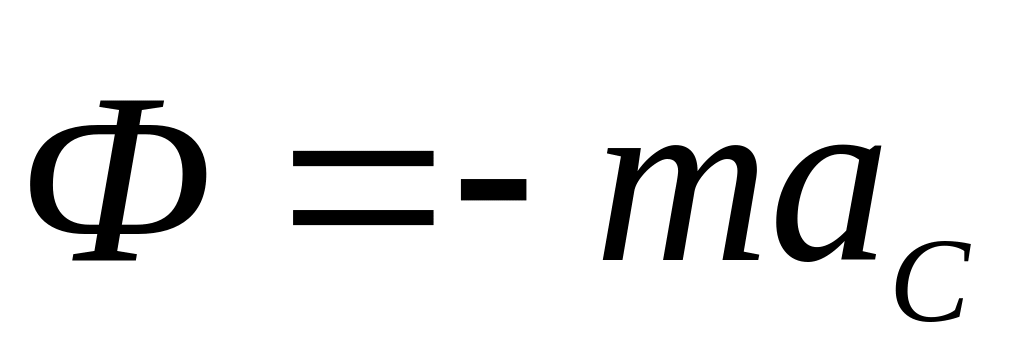

Модуль равнодействующей равен произведению массы тела на модуль ускорения его центра масс, а ее направление противоположно этому ускорению.

2. Вращение вокруг неподвижной оси. Совместим ось Oz системы координат Oxyz с осью вращения тела, а оси Ox и Oy жестко свяжем с ним. Так как векторы и 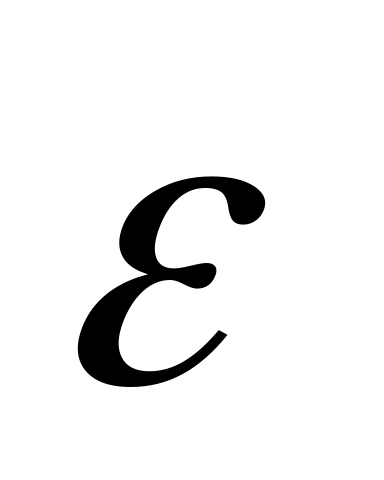направлены вдоль оси Oz, то их проекции на оси x и y равны нулю: _x=_y=0, _x=_y=0, а _z=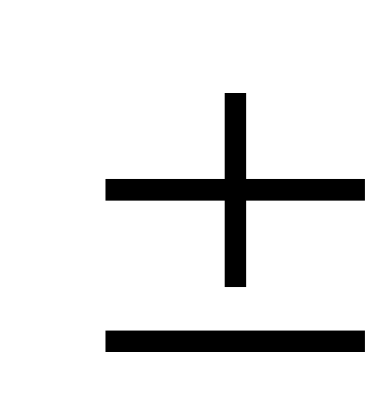 . Подставляя эти значения в (11.12), получаем:

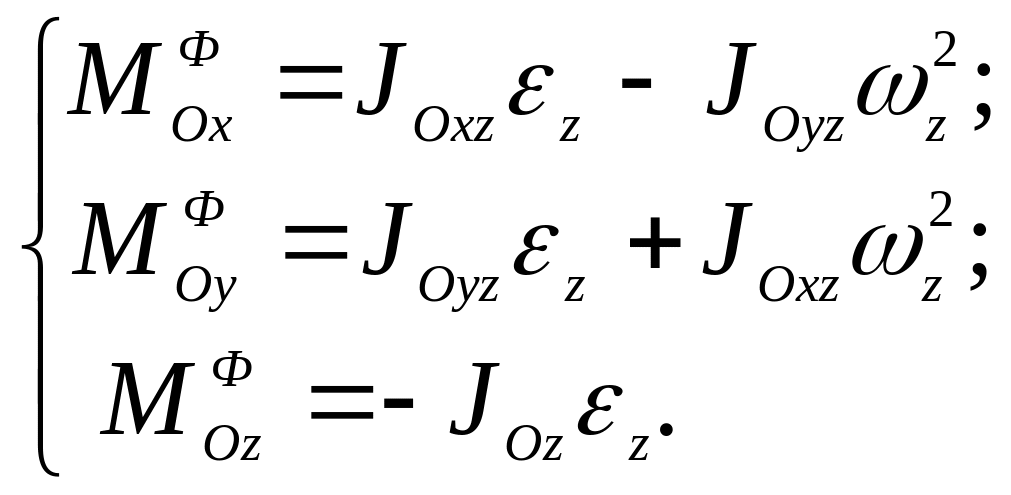. (11.14)

Если центр тяжести тела не лежит на оси вращения и, следовательно, , то главный вектор сил инерции , а его проекции на оси подвижной системы координат определяются по формулам (11.7).

3. Плоское движение. Предположим, что ось Cz подвижной системы координат Сxyz перпендикулярна плоскости материальной симметрии тела, все точки которого движутся в плоскостях, параллельных этой плоскости. Пусть при этом оси Cx и Cy лежат в плоскости материальной симметрии. Плоское движение тела можно представить состоящим из поступательного движения вместе с центром масс С тела и вращения вокруг подвижной оси Сz, проходящей через центр масс.

Главный вектор сил инерции определяется по формуле (11.7) .

В силу материальной симметрии тела J_xz=J_yz=0. Кроме того, очевидно, что _x=_y=0, _x=_y=0. Тогда из формул (11.12) находим проекции на оси подвижной системы координат главного момента сил инерции:

, , . (11.15)

Определение динамических реакций опор твердого тела, вращающегося вокруг неподвижной оси

Рассмотрим твердое тело массы m, которое под действием некоторой системы внешних сил , ,…, неравномерно вращается вокруг неподвижной вертикальной оси Az (рис. 13.2). Будем считать, что в данный момент времени тело имеет угловую скорость  и угловое ускорение . Поставим перед собой задачу определить опорные реакции , , подпятника А и , подшипника В.

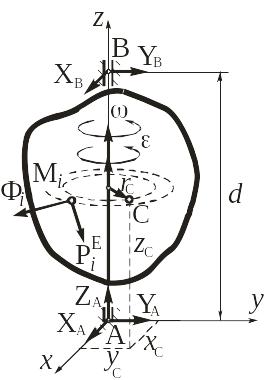
Рис. 11.2

Приложим к каждой точке М_i тела силу инерции . Согласно принципу Германа-Эйлера-Даламбера внешние задаваемые силы, реакции связей и силы инерции точек тела должны удовлетворять уравнениям (11.5). В рассматриваемом случае эти уравнения с учетом (11.14) принимают вид:

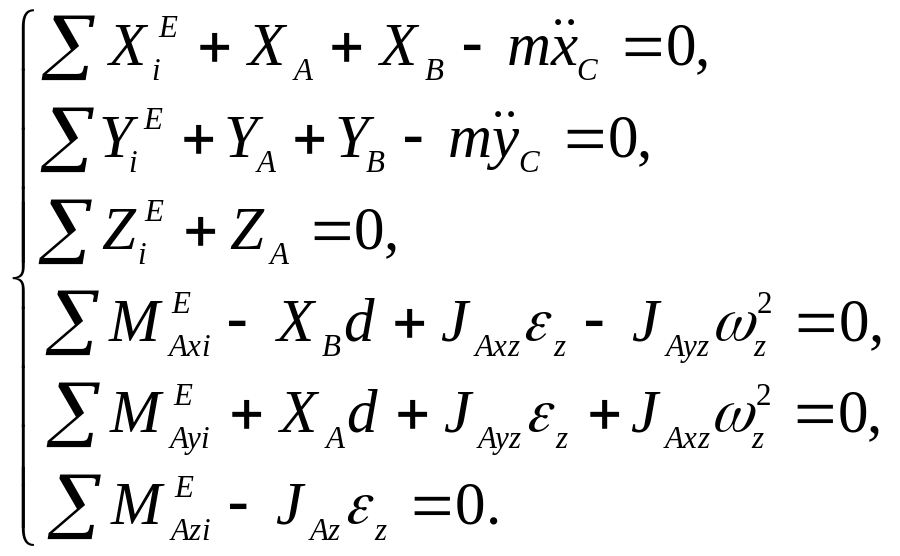. (11.16)

Здесь J_Axz, J_Ayz − центробежные моменты инерции тела относительно осей Ax и Az и осей Ay и Az, , − проекции ускорения центра масс С тела на оси x и y системы координат Axyz, жестко связанной с телом и вращающейся вместе с ним.

Вектор ускорения центра масс тела определяется по формуле:

,

где − радиус-вектор центра масс.

Спроецируем на оси координат:

;

.

В результате система уравнений (11.16) принимает вид:

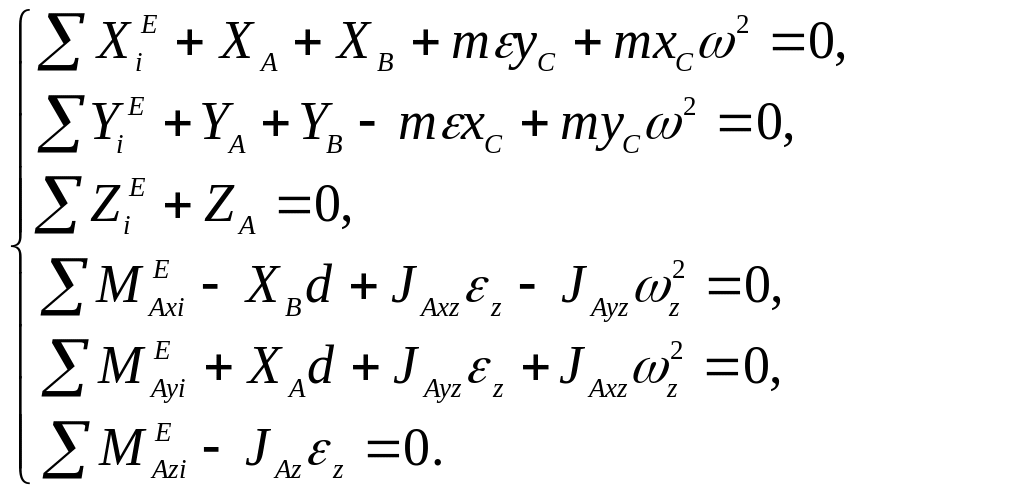. (11.17)

Первые пять уравнений системы (11.17) позволяют найти пять составляющих реакций подшипника и подпятника. Силы , , и содержат не только статические составляющие, зависящие от задаваемых сил, но и динамические составляющие, вызываемые силами инерции. Динамические составляющие зависят, в частности, от угловой скорости и углового ускорения вращающегося тела и могут достигать больших значений.

Уравнения (11.17) позволяют выявить условия, при которых динамические составляющие опорных реакций подпятника А и подшипника В равны нулю. Для получения этих условий приравняем нулю суммы членов, соответствующих силам инерции, в уравнениях (11.17):

, , (11.18)

, . (11.19)

Из (11.18) находим: x_C=0, y_C=0. Это означает, что центр тяжести тела должен находиться на оси вращения.

Решение уравнений (11.19) приводит к результату: J_Axz=0, J_Ayz=0, т.е. ось z должна быть главной осью инерции тела для точки А.

Объединяя эти результаты, устанавливаем, что, если ось вращения тела является главной центральной осью инерции, то динамические составляющие его опорных реакций равны нулю.

Для того, чтобы выполнить это условие, деталям механизмов и машин придают форму тел вращения. При этом ось вращения детали должна совпадать с ее осью симметрии. Если же из-за неточности изготовления не удается совместить ось вращения с главной центральной осью инерции, то эта ошибка устраняется специальными приемами (статической и динамической балансировками).