Уравнения Лагранжа II рода

Предположим, что механическая система, состоящая из n точек, имеет s степеней свободы, и на нее наложены голономные двусторонние стационарные идеальные связи. Движение такой системы относительно заданной системы отсчета описывается совокупностью из s обобщенных координат q₁, q₂,…,q_s, являющихся функциями времени: q_j= q_j(t) (j=1,…,s).

Радиус-вектор i-той точки системы является некоторой функцией обобщенных координат , представляя собой сложную функцию времени. Поэтому скорость i-той точки определяется по формуле (15.1).

Кинетическая энергия механической системы определяется по формуле:

.

Найдем частные производные от кинетической энергии Т по обобщенной координате и обобщенной скорости :

; (15.9)

. (15.10)

Если в (15.10) подставить (15.2), то получим: .

Продифференцируем это выражение по времени:

. (15.11)

Преобразуем первое и второе слагаемые этого равенства. Первое слагаемое с учетом выражения (15.4) принимает вид:

. (15.12)

Теперь рассмотрим второе слагаемое в выражении (15.11), но предварительно найдем две производные:

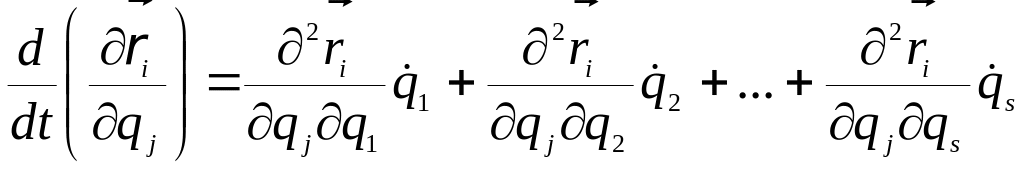; (15.13)

. (15.14)

Сравнивая равенства (15.13) и (15.14), получаем:

. (15.15)

Таким образом, второе слагаемое в выражении (15.11) с учетом формулы (15.8) приобретает вид:

. (15.16)

Подставим (15.12) и (15.16) в (15.11) и получим: .

Окончательно, уравнения Лагранжа II рода записывают следующим образом:

(j=1,…,s). (15.17)

Уравнения Лагранжа II рода представляют собой удобный аппарат для получения дифференциальных уравнений движения механических систем с s степенями свободы. Особенностью этих уравнений является то, что они не включают в себя опорных реакций.

Уравнения Лагранжа II рода для случая сил, имеющих потенциал

Рассмотрим механическую систему с s степенями свободы, движение которой ограничено голономными двусторонними стационарными идеальными связями. Пусть при этом на точки системы действуют силы, имеющие потенциал. В таком случае проекции X_i, Y_i, Z_i сил на оси координат выражаются формулами:

; , , (15.18)

где =(x,y,z)– потенциальная энергия системы.

Подставим (15.18) в (15.4):

.

Таким образом, в случае сил, имеющих потенциал, обобщенная сила, соответствующая j-той обобщенной координате, равна взятой со знаком минус частной производной от потенциальной энергии механической системы по этой координате: (j=1,…,s). (15.19)

Если на механическую систему действуют только консервативные силы, то уравнения Лагранжа II рода (15.17) приобретают вид:

(j=1,…,s). (15.20)

Эти уравнения можно преобразовать путем введения так называемой функции Лагранжа L=T–, (15.21)

называемой еще кинетическим потенциалом.

Так как потенциальная энергия системы  не зависит от обобщенных скоростей, то . (15.22)

Выразив Т из (15.21) и подставив в (15.20) с учетом (15.22), получим уравнения Лагранжа II рода для консервативных систем:

(j=1,…,s). (15.23)

Лекция 15

Устойчивость положения равновесия механической системы. Теорема Лагранжа-Дирихле. Критерий Сильвестра

Среди всех процессов, протекающих в природе и современной технике, огромное значение имеют колебательные движения различных динамических систем (движение электрического заряда в колебательном контуре, вибрации станков, различных приборов, деталей инженерных сооружений, транспортных средств и т.д.). При неблагоприятном стечении обстоятельств колебания механических систем могут вызвать большие деформации и напряжения в их элементах, а также привести к быстрому износу и даже разрушению конструкций.

В теории колебаний исследуются колебательные явления в динамических системах различной природы (механической, электрической, биологической и т.д.), выявляются их общие свойства, а также связь между движением и параметрами колебательных систем. На основе положений, устанавливаемых теорией колебаний, появляется возможность для создания приборов, машин, конструкций и специальных устройств (гасителей колебаний, вибростендов, вибротранспортеров, виброуплотнителей бетона и т.д.) с оптимальными параметрами, при которых обеспечивается максимальная производительность технологических процессов.

Кинетическая энергия механической системы с одной, двумя и s степенями свободы

Выясним, какова зависимость кинетической энергии механической системы от обобщенных скоростей .

Рассмотрим механическую систему с s степенями свободы с голономными стационарными связями. Радиус-вектор i-той точки системы является функцией s обобщенных координат: . Поэтому скорость каждой точки системы определяется по формуле (17.1)

. (16.1)

Подставим это выражение в (10.7):

.

Отсюда видно, что кинетическая энергия системы с s степенями свободы, движение точек которой ограничено голономными стационарными связями, представляет собой положительно определенную однородную квадратичную форму обобщенных скоростей:

, (16.2)

где − так называемые коэффициенты инерции системы, в общем случае являющиеся нелинейными функциями обобщенных координат . Очевидно, что эти коэффициенты симметричны относительно индексов k и l ( ).

Кинетическая энергия (16.2) может быть записана в матричной форме

, (16.3)

где 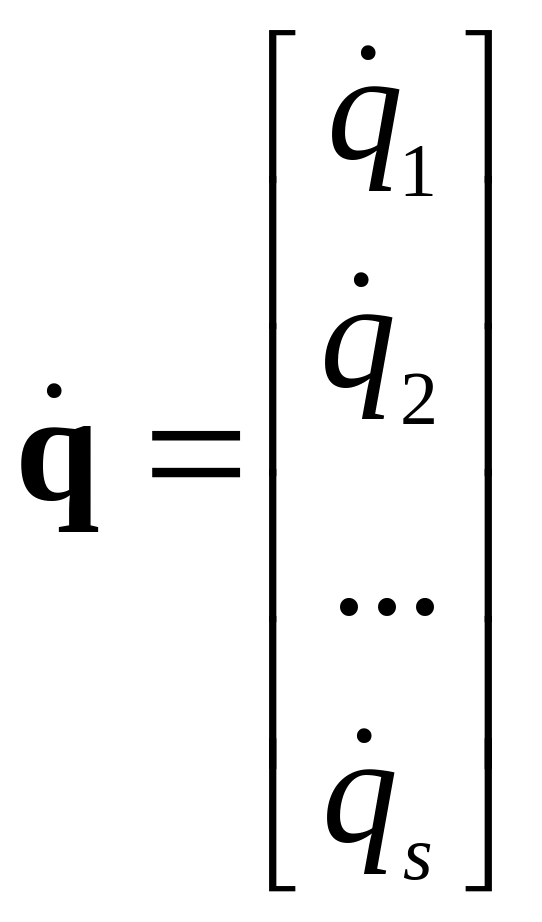− вектор-столбец обобщенных скоростей; − транспонированный вектор-столбец обобщенных скоростей (вектор-строка); − матрица инерции системы.

Матрица А является симметричной (А_ij=A_ji). Кроме того, можно доказать, что матрица А является невырожденной ( ).

Вид зависимости (16.2) кинетической энергии Т от обобщенных скоростей позволяет утверждать, что уравнения Лагранжа II рода (15.17) разрешимы относительно старших производных и после подстановки Т в эти уравнения получается система s обыкновенных дифференциальных уравнений второго порядка относительно обобщенных координат, всегда линейная по обобщенным ускорениям. Однако, в целом система этих дифференциальных уравнений в общем случае будет нелинейной, в частности, из-за зависимости коэффициентов инерции A_k,l от обобщенных координат.

Во многих случаях можно линеаризовать систему дифференциальных уравнений, разложив каждый из коэффициентов инерции A_kl в ряд Маклорена по степеням обобщенных координат:

. (16.4)

Индекс 0 соответствует начальному положению системы, от которого отсчитываются значения обобщенных координат.

Будем рассматривать настолько малые отклонения механической системы от начального положения с такими малыми по модулю обобщенными скоростями, что в выражении кинетической энергии можно оставить только члены наинизшего порядка малости, а именно − второго порядка (порядки малости обобщенных координат и обобщенных скоростей предполагаются одинаковыми). Тогда в разложении (18.4) можно ограничиться только первыми постоянными слагаемыми:

.

Обозначим эти постоянные коэффициенты (коэффициенты инерции) a_kl и перепишем выражение (18.2) кинетической энергии механической системы с s степенями свободы в виде:

. (16.5)

Для системы с одной степенью свободы получим:

, (16.6)

где а − коэффициент инерции системы; − обобщенная скорость.

Для системы с двумя степенями свободы кинетическая энергия принимает вид:

. (16.7)

Линеаризованная матрица коэффициентов инерции в этом случае записывается следующим образом:

, (16.8)

причем a₁₂= a₂₁.

Потенциальная энергия механической системы с одной, двумя и s степенями свободы

Рассмотрим механическую систему, имеющую s степеней свободы, и пусть на эту систему наложены голономные стационарные связи. Потенциальная энергия  подобной системы является некоторой функцией обобщенных координат:

Предположим, что механическая система имеет положение равновесия, от которого будем отсчитывать обобщенные координаты, то есть будем считать, что в положении равновесия q₁=q₂=…=q_s=0. Если функция непрерывна в окрестности положения покоя и имеет все производные по обобщенным координатам, то ее можно разложить в ряд Маклорена по степеням обобщенных координат:

. (16.9)

Нижний индекс 0 в этом выражении означает, что соответствующие производные вычислены в положении равновесия системы.

В главе XIX отмечалось, что потенциальная энергия системы определяется с точностью до постоянного слагаемого, которое, в частности, можно принять равным нулю. Поэтому будем полагать, что

П(0)=0. (16.10)

В положении покоя механической системы скорости ее точек равны нулю ( ). Из (14.1) следует, что в этом случае все обобщенные скорости . Тогда слагаемые, стоящие в левой части уравнений Лагранжа II рода (15.17), обращаются в нуль. Отсюда следует, что если голономная механическая система со стационарными связями находится в равновесии, то все обобщенные силы, соответствующие s обобщенным координатам, равны нулю:

(j=1,…,s).

В случае сил, имеющих потенциал, обобщенная сила, соответствующая j-той обобщенной координате, определяется по формуле (15.20):

(j=1,…,s).

Таким образом, получаем, что в положении покоя

(j=1,…,s). (16.11)

Вследствие этого

.

Будем рассматривать настолько малые отклонения механической системы от начального положения, что в выражении потенциальной энергии можно сохранить величины наинизшего порядка малости (второго). В результате, сохраняя в разложении (16.9) члены порядка не выше второго и учитывая соотношения (16.10) и (16.11), приходим к выражению

.

Или

, (16.12)

где − коэффициенты жесткости системы (c_kl=c_lk).

Выражение (16.12) показывает, что потенциальная энергия механической системы с s степенями свободы в этом случае представляет собой однородную квадратичную форму обобщенных координат.

Потенциальную энергию (16.12) иногда удобно записать в матричной форме

, (16.13)

где − вектор-столбец обобщенных координат; Т − индекс транспонирования;

(16.14)

− матрица жесткости системы.

Матрица жесткости С является симметричной (с_ij=с_ji).

Потенциальная энергия системы с одной степенью свободы:

, (16.15)

где с − коэффициент жесткости системы; − обобщенная координата.

Для системы с двумя степенями свободы потенциальная энергия может быть записана в форме:

. (16.16)

Матрица коэффициентов жесткости в этом случае выглядит так:

, (16.17)

причем с₁₂=с₂₁.

Устойчивость положения равновесия механической системы

Колебания механической системы могут происходить либо около положения равновесия, либо вокруг некоторого стационарного движения.

Колебания около положения покоя возникают в случае, если это положение устойчиво. Поэтому при изучении колебательного движения механической системы следует найти положения покоя системы и исследовать их устойчивость.

Рассмотрим механическую систему с s степенями свободы, движение точек которой ограничено стационарными голономными связями.

Пусть на систему действуют только силы, имеющие потенциал. Тогда уравнения равновесия такой механической системы имеют вид (16.11):

(j=1,…,s). (16.18)

Эти уравнения можно рассматривать как систему s уравнений для определения тех значений обобщенных координат , при которых механическая система может находиться в равновесии.

Однако, не все эти положения практически осуществимы. Например, шарик, показанный на рис. 16.18 имеет три положения покоя − А, В и С. Очевидно, что верхние положения А и С равновесия шарика практически нельзя реализовать, так как они неустойчивы, а нижнее положение В устойчиво и легко реализуемо.

Рис. 16.1

Уравнения (16.18) показывают, что положениями покоя консервативной механической системы являются те положения, в которых ее потенциальная энергия достигает экстремальных значений.

Определим понятие устойчивости положения равновесия.

Состояние покоя механической системы называется устойчивым, если система, будучи выведенной из этого положения, совершает колебания около него (система, получив малые начальные отклонения от положения равновесия и малые начальные скорости, в дальнейшем движется так, что обобщенные координаты и обобщенные скорости по модулю остаются малыми величинами). Математически строгое определение устойчивости впервые было дано А.М. Ляпуновым.

Состояние покоя механической системы называется неустойчивым, если система, получившая сколь угодно малое отклонение от положения покоя, удаляется от этого положения (при этом не возникает колебаний около этого положения равновесия).

Состояние покоя механической системы называется безразличным, если отклонение системы от положения покоя на сколь угодно малую величину приводит ее в новое положение равновесия.

Для консервативных механических систем, подчиненных голономным стационарным связям, критерии устойчивости состояния покоя выводятся в зависимости от потенциальной энергии этих систем.

Теорема Лагранжа-Дирихле. Критерий Сильвестра

Достаточные условия устойчивости состояния покоя механической системы содержатся в теореме Лагранжа-Дирихле: те положения покоя консервативной механической системы с идеальными стационарными связями, в которых потенциальная энергия достигает минимума, являются устойчивыми положениями равновесия.

Доказательство этой теоремы получается как следствие более общей теоремы Ляпунова об устойчивости движения.

Таким образом, для выяснения вопроса, является ли данное положение покоя устойчивым, необходимо определить, имеет ли механическая система в этом положении минимум.

Для системы с одной степенью свободы задача об определении минимума решается очень просто. Нужно убедиться в том, что вторая производная от потенциальной энергии по обобщенной координате (если эта производная существует), вычисленная в положении равновесия, положительна:

. (16.19)

Применение этого требования к (18.15) приводит к тому, что формальным признаком устойчивости системы с одной степенью свободы является положительность ее коэффициента жесткости с. В реальных механических системах знак коэффициента жесткости может зависеть от одного или нескольких параметров. Поэтому положение равновесия системы может быть устойчивым или неустойчивым в зависимости от комбинации значений этих параметров.

Если окажется, что , то в этом случае нужно последовательно вычислять следующие производные более высокого порядка .

Если первая, не равная нулю производная от потенциальной энергии по обобщенной координате, вычисленная в положении покоя, имеет четный порядок и положительна, то это положение устойчиво.

Если же первая, не равная нулю производная от потенциальной энергии по обобщенной координате при q=0 имеет нечетный порядок, то потенциальная энергия в этом положении не имеет ни максимума, ни минимума.

Для консервативных механических систем с одной степенью свободы при нарушении условий теоремы Лагранжа-Дирихле получаем противоположное утверждение, которое формулируется, как теорема о неустойчивости положения равновесия (теорема Четаева Н.Г.).

Если в изолированном положении равновесия потенциальная энергия не имеет минимума, то это положение неустойчиво.

Для консервативной механической системы, имеющей s степеней свободы, устойчивость положения покоя также определяется из условия минимума потенциальной энергии системы. Однако, критерий устойчивости имеет более сложный вид.

Потенциальная энергия консервативной механической системы в положении равновесия (при q₁=q₂=…=q_s=0) будет иметь изолированный минимум, если ее потенциальная энергия (16.12) представляет собой определенно положительную квадратичную форму обобщенных координат.

Квадратичная форма начала координат называется определенно положительной (определенно отрицательной), если в этой окрестности она принимает положительные (отрицательные) значения и обращается в нуль только в начале координат.

Необходимые и достаточные условия положительной определенности потенциальной энергии определяются критериями Сильвестра: для положительной определенности потенциальной энергии консервативной механической системы с s степенями свободы требуется, чтобы все главные диагональные миноры определителя ее матрицы жесткости С (16.14) были положительны, то есть:

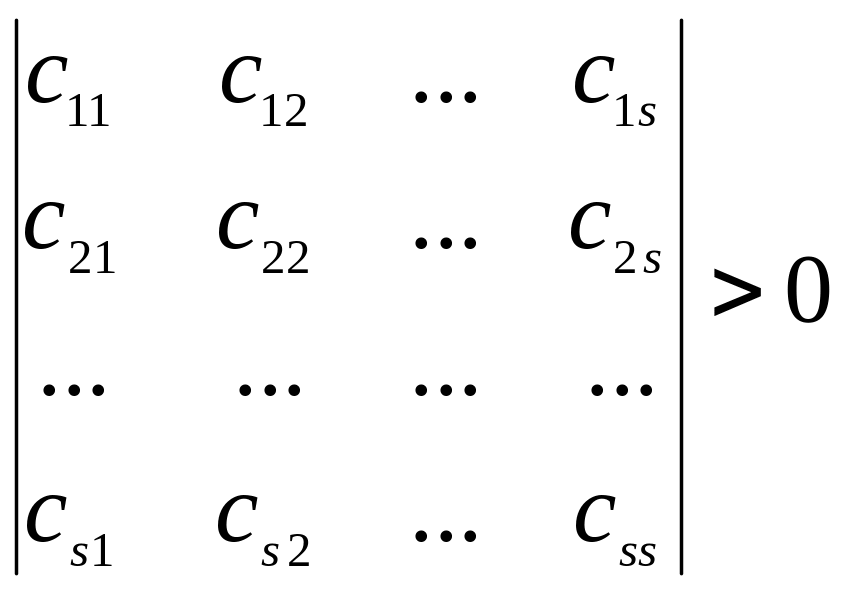; ;… . (16.20)

Критерий (16.20) является недостаточным для определения устойчивости равновесия неконсервативных систем. В этом случае приходится рассматривать решения так называемых дифференциальных уравнений возмущенного движения системы, происходящего около положения покоя, и по свойствам решений судить об устойчивости этого положения равновесия.

Таким образом, при решении задачи о нахождении положений равновесия механической системы и исследований их устойчивости необходимо:

1. выбрать обобщенные координаты и составить выражение потенциальной энергии 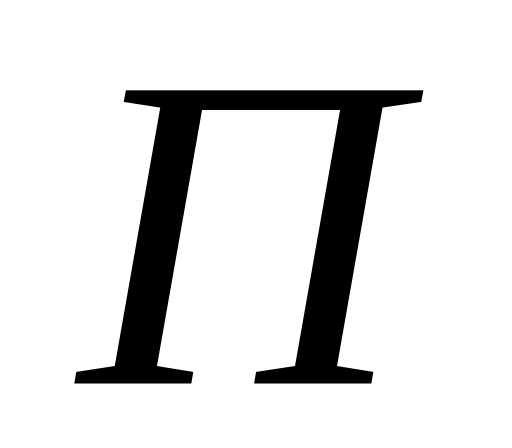системы;

2. разложить в ряд Маклорена по степеням и составить матрицу жесткости ;

3. применить критерий Сильвестра, составив определители (16.20). Если все , то положение равновесия устойчиво.