С явлением резонанса связана и опасность: внешняя э.д.с. или напряжение могут быть малы, однако при этом напряжения на отдельных элементах контура (на емкости или индуктивности) могут достигать опасного для жизни значения. Об этом необходимо всегда помнить!

§ 11.4. Переменный ток

Полное сопротивление (импеданс). Установившиеся вынужденные электрические колебания можно рассматривать как протекание в цепи, обладающей емкостью, индуктивностью и активным сопротивлением R, переменного тока. Под действием внешнего напряжения (оно играет роль внешней э.д.с. )

Задача сводится к определению амплитуды силы тока и сдвига тока по фазе относительно U.

Полученное выражение для амплитуды силы тока Im( ) можно формально толковать как закон Ома для амплитудных значений тока и напряжения. Стоящую в знаменателе этого выражения величину, имеющую размерность сопротивления, обозначают буквой Z и называют полным сопротивлением

Видно, что при 0 1/LC это сопротивление минимально и равно активному сопротивлению R. Величину, стоящую в круглых скобках формулы (11.46), обозначают X и называют

реактивным сопротивлением:

При этом величину L называют индуктивным сопротивлением, а величину 1/ С — емкостным сопротивлением. Их обозначают соответственно XL и ХC. Итак,

XL L, XC 1/ C, X XL – XC, Z 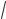R2 X 2 . (11.48)

Заметим, что индуктивное сопротивление растет с увеличением частоты , а емкостное — уменьшается. Когда говорят, что в цепи отсутствует емкость, то это надо понимать в смысле отсутствия емкостного сопротивления, которое равно 1/ С и, следовательно, обращается в нуль, если С (при замене конденсатора закороченным участком).

И последнее. Хотя реактивное сопротивление измеряют в тех же единицах, что и активное, между ними существует принципиальное различие. Оно заключается в том, что только активное сопротивление определяет необратимые процессы в цепи, такие, например, как преобразование электромагнитной энергии в джоулеву теплоту.

Мощность, выделяемая в цепи переменного тока. Мгновенное значение мощности равно произведению мгновенных зна-

Поскольку cos( t – ) cos t cos sin t sin , преобразуем (11.49) к виду

P(t) UmIm (cos2 t cos sin t cos t sin ).

Практический интерес имеет среднее за период колебания значение мощности. Учитывая, что Ucos2 tV 1/2 и Usin t cos tV0, получим:

Это выражение можно привести к иному виду, если принять во внимание, что из векторной диаграммы (см. рис. 11.4) следует Um cos RIm. Поэтому

Такую же мощность развивает постоянный ток I I m /2. Величины

называют действующими (или эффективными) значениями тока и напряжения. Все амперметры и вольтметры градуированы по действующим значениям тока и напряжения.

Выражение средней мощности (11.50) через действующие значения напряжения и тока имеет вид

где множитель cos принято называть коэффициентом мощности. Таким образом, выделяемая в цепи мощность зависит не только от напряжения и силы тока, но еще и от сдвига фаз между током и напряжением.

При /2 значение UPV 0, каковы бы ни были величины U и I. В этом случае энергия, передаваемая за четверть периода от генератора во внешнюю цепь, в точности равна энергии, передаваемой из внешней цепи в генератор в течение следующей четверти периода, и вся энергия бесполезно «колеблется» между генератором и внешней цепью.

Зависимость мощности от cos необходимо учитывать при проектировании линий электропередачи на переменном токе. Если питаемые нагрузки имеют большое реактивное сопротивление X, то cos может быть заметно меньше единицы. В этих случаях для передачи потребителю нужной мощности (при данном напряжении генератора) необходимо увеличить ток I, а это приводит к возрастанию бесполезных потерь энергии в подводящих проводах. Поэтому всегда нужно стремиться распределять нагрузки, индуктивности и емкости так, чтобы cos был по возможности близок к единице. Для этого достаточно сделать реактивное сопротивление Х как можно меньше, т. е. обеспечить равенство индуктивного и емкостного сопротивле-

ний (XL XC).

В заключение заметим, что понятие активного сопротивления шире, чем понятие электрического сопротивления проводников, образующих цепь. Последнее обусловливает переход

энергии тока только в джоулеву теплоту, но возможны и другие превращения этой энергии, например в механическую работу (электромоторы). Активное сопротивление тогда уже не сводится к электрическому сопротивлению, а обычно значительно превышает его.

Задачи

11.1.Собственные незатухающие колебания. В контуре, состоящем из конденсатора емкости С и катушки с индуктивностью L, происходят свободные незатухающие колебания с амплитудой напря-

жения на конденсаторе Um. Найти э.д.с. самоиндукции в катушке в моменты, когда ее магнитная энергия оказывается равной

электрической энергии конденсатора. Решение. Согласно закону Ома

RI U s,

где U — напряжение на конденсаторе (U 1 – 2). В нашем случае R 0, поэтому s – U.

Остается найти напряжение U в моменты, когда электрическая энергия конденсатора равна магнитной энергии катушки. При этом условии можно записать:

откуда |U| Um/2.

В результате имеем | s | Um/2.

11.2.Колебательный контур состоит из катушки с индуктивностью L и незаряженного конденсатора емкости С. Активное сопротивление контура R 0. Катушка находится в постоянном магнитном поле так, что полный магнитный поток, пронизывающий все ее витки, равен Ф. В момент t 0 магнитное поле резко выключили. Найти ток в контуре как функцию времени t.

Решение. При резком выключении внешнего магнитного поля в момент t = 0 появится индукционный ток, но конденсатор будет еще не заряженным. Поэтому согласно закону Ома

I0 — начальный ток (непосредственно после выключения поля).

(второе условие следует из уравнения (1), ибо в начальный момент t 0 конденсатор был не заряжен). Из этих условий найдем0, Im I0. В результате

I I0 cos 0t (Ф/L) cos 0t,

где 0 1/LC .

11.3.В колебательном контуре происходят свободные незатухающие колебания с энергией W. Пластины конденсатора медленно раздвинули так, что частота колебаний увеличилась в , раз. Какую работу совершили при этом против электрических сил?

Решение. Будем исходить из того, что приращение энергии W колебаний контура происходит за счет работы против электрических сил. Определим эту работу сначала за малый промежуток времени t, в течение которого расстояние между пластинами увеличилось на dh:

где UFV — среднее за t значение модуля силы электрического взаимодействия между пластинами. Так как E q/2 0S и, согласно формуле C 0S/h, dh 0S d(1/C), то

В данном случае (процесс медленный) возьмем промежуток времени t таким, чтобы Т I t I t, где Т — период колебаний, t — вре-

306 Глава 11

мя всего процесса. При этом условии колебания за время t можно

2 2

считать практически гармоническими и Uq V qm /2 WC, поскольку W qm2 /2C. С учетом этого перепишем (2) и приравняем полученное выражение к dW:

Проинтегрировав последнее уравнение, найдем ln( W C ) const. Остается учесть, что T 1/C , и мы получим

Это важное соотношение и справедливо оно только при медленном процессе.

Искомую работу можно представить как приращение колебательной энергии контура: A = W – W. Воспользовавшись формулой (4), получим:

AW( / – 1) W(, – 1).

11.4.Добротность контура. Колебательный контур с малым затуханием имеет емкость С и индуктивность L. На поддержание в нем незатухающих гармонических колебаний с амплитудой напря-

жения на конденсаторе Um необходимо подводить среднюю мощность UРV. Найти добротность контура.

Решение. Вследствие малости затухания воспользуемся формулой (11.23):

где W CUm2 /2 и dW UРVT, T — период затухающих колебаний. В нашем случае T T0 2 LC . После подстановки этих выражений в (1) получим

11.5.Затухающие колебания. В колебательном контуре имеется конденсатор емкости С, катушка с индуктивностью L, активное сопротивление R и ключ. При разомкнутом ключе конденсатор зарядили, а затем ключ замкнули. Найти отношение напряжения на конденсаторе к его амплитудному значению в начальный момент (сразу после замыкания ключа).

Решение. Напряжение на конденсаторе будет зависеть от времени так же, как и заряд, поэтому запишем

В начальный момент t 0 напряжение U(0) Um cos , где Um — амплитуда в этот момент. Нам надо найти U(0)/Um, т. е. cos .

Для этого воспользуемся другим начальным условием: в момент

.

t 0 ток I q 0 . Так как q CU, то достаточно продифференцировать (1) по времени и полученное выражение при t 0 приравнять к нулю. Получим – = cos – sin 0, откуда tg

–=/ . Поэтому искомое отношение

Величины U(0) и Um показаны на рис. 11.8.

Принимая во внимание, что 1 14 =1 , преобразуем (2) к виду

U( 0)/Um 1 ( =/ )2 1 R 2C/4L ,

где учтено, что = R/2L и 20 1/LC.

11.6. В колебательном контуре с емкостью С и индуктивностью L совершаются затуха-

ющие колебания, при которых ток меняется со временем по закону I(t) = Im е–=tsin t. Найти напряжение на конденсаторе в зависимости от времени.

Решение. Выберем положительное направление обхода контура

формулу можно переписать так:

После подстановки сюда выражения для I(t) и его производной получим

UC RIm e=t ( = sin t cos t). 2=

Преобразуем выражение в скобках к синусу. Для этого умножим и разделим его на 2 =2 0 , а затем введем угол по формулам

Тогда

где угол согласно (1) находится во второй четверти, т. е. принимает значения /2 < < . Таким образом, напряжение на конденсаторе отстает по фазе от тока.

11.7.Установление колебаний. Катушку с индуктивностью L и активным сопротивлением R подключили в момент t 0 к внешнему

напряжению U Um cos t. Найти ток в цепи как функцию времени t.

.

Решение. В данном случае RI U LI , или

.

I ( R /L )I (Um /L ) cos t.

Решение этого уравнения есть общее решение однородного уравнения плюс частное решение неоднородного:

где А — произвольная постоянная, а угол определяется условием (11.36): tg L/R.

Постоянную А находим из начального условия I(0) 0.

R 2 2 L2

При достаточно большом t второе слагаемое в квадратных скобках становится пренебрежимо малым, и мы получаем установившееся решение I(t) T cos( t – ).

11.8.Вынужденные колебания. Участок цепи, состоящий из последовательно соединенных конденсатора и активного сопротивления R, подключили к внешнему переменному напряжению с ампли-

тудой Um. При этом амплитуда установившегося тока оказалась равной Im. Найти разность фаз между током и внешним напряжением.

11.9.Цепь переменного тока, содержащая последовательно соединенные конденсатор и катушку с активным сопротивлением, подключена к внешнему переменному напряжению, частоту которо-

го можно менять, не меняя его амплитуды. При частотах 1 и 2 амплитуды силы тока в цепи оказались одинаковыми. Найти ре-

зонансную частоту тока.

Решение. Согласно (11.35) амплитуды будут одинаковыми при условии

Максимуму резонансной кривой тока соответствует частота, равная собственной частоте 0 1/LC . Пусть 1 < 0 < 2 (можно предположить и наоборот, от этого окончательный результат не

изменится), тогда равенство (1) можно переписать, сняв модули, так: 20 / 1 1 2 20 / 2 , или

После сокращения обеих частей этого равенства на 2 1 получим: 1 20 / 1 2, откуда

0 1 2 .

11.10. Векторная диаграмма. Цепь, состоящую из последовательно соединенных конденсатора емкости С и катушки с активным сопротивлением R и с индуктивностью L, подключили к внешнему гармоническому напряжению с амплитудой Um и частотой . Считая, что ток в цепи опережает по фазе внешнее напряжение, построить соответствующую векторную диаграмму и с помощью нее найти

амплитуду напряжения на катушке.

Решение. Векторная диаграмма для данного случая имеет вид, показанный на рис. 11.11. Из этой диаграммы сразу вид-

Рис. 11.11 но, что амплитуда напряжения на катушке

ULRm Im R 2 2 L2 , где Im Um /R 2 ( L 1/ C )2 .

Напряжение на катушке при наличии активного сопротивления опережает ток по фазе менее чем на /2.

11.11.Мощность в цепи переменного тока. Цепь, состоящую из последовательно соединенных безындукционного сопротивления R и катушки с некоторым активным сопротивлением, подключили к сети с действующим напряжением U. Найти тепловую мощность, выделяемую в катушке, если действующие напряжения на сопротивлении R и катушке равны соответственно U1 и U2.

Решение. Воспользуемся векторной диаграммой, которая дана на рис. 11.12. Из этой диаграммы согласно теореме косинусов имеем