§ 5.1. Плотность тока. Уравнение непрерывности

Электрический ток. В этой главе мы ограничимся рассмотрением тока проводимости в проводящей среде, главным образом в металлах. Электрический ток, как известно, представляет собой перенос заряда через ту или иную поверхность S (например, через сечение проводника).

Носителями тока в проводящей среде могут быть электроны (в металлах), либо ионы (в электролитах), либо другие частицы. При отсутствии электрического поля носители тока совершают хаотическое движение и через любую воображаемую поверхность S проходит в обе стороны в среднем одинаковое число носителей того и другого знака, так что ток через поверхность S равен нулю. При включении же электрического поля на хаотическое движение носителей накладывается упорядоченное движение с некоторой средней скоростью u и через поверхность S появится ток. Таким образом, электрический ток — это, по существу, упорядоченный перенос электрических зарядов.

Количественной мерой электрического тока служит сила тока I, т. е. заряд, переносимый сквозь рассматриваемую поверхность S в единицу времени:

I dq/dt.

Единицей силы тока является ампер (А).

Плотность тока. Электрический ток может быть распределен по поверхности, через которую он протекает, неравномерно. Поэтому для более детальной характеристики тока вводят вектор плотности тока j. Модуль этого вектора численно равен отношению силы тока dI через элементарную площадку, распо-

ложенную в данной точке перпендикулярно направлению движения носителей, к ее площади dS : j dI/dS . За направление вектора j принимают направление вектора скорости u упорядоченного движения положительных носителей (или направление, противоположное направлению вектора скорости упорядоченного движения отрицательных носителей). Если носителями являются как положительные, так и отрицательные заряды, то плотность тока определяется формулой

где + и – — объемные плотности положительного и отрицательного зарядов-носителей; u+ и u– — скорости их упорядоченного движения. В проводниках же, где носителями являются только электроны ( –< 0 и u+ = 0), плотность тока

Поле вектора j можно изобразить графически с помощью линий тока (линий вектора j), которые проводят так же, как и линии вектора Е.

Зная вектор плотности тока в каждой точке интересующей нас поверхности S, можно найти и силу тока через эту поверхность как поток вектора j:

Сила тока I является величиной скалярной и алгебраической. Ее знак, как видно из формулы (5.3), определяется, кроме всего прочего, выбором направления нормали в каждой точке поверхности S, т. е. выбором направления векторов dS. При изменении направления всех векторов dS на противоположное величина I меняет знак.

Уравнение непрерывности. Представим себе в некоторой проводящей среде, где течет ток, замкнутую поверхность S. Для замкнутых поверхностей векторы нормалей, а следовательно, и векторы dS принято брать наружу, поэтому интеграл KjdS дает заряд, выходящий в единицу времени наружу из объема V, охватываемого поверхностью S. В силу закона сохранения заряда этот интеграл равен убыли заряда в единицу време-

Это соотношение называют уравнением непрерывности. Оно является, по существу, выражением закона сохранения электрического заряда.

В случае стационарного (постоянного) тока распределение зарядов в пространстве должно оставаться неизменным, т. е. в правой части (5.4) dq/dt = 0. Следовательно, для постоянного тока

иначе говоря, линии вектора j в этом случае нигде не начинаются и нигде не заканчиваются. Мы говорим, что в случае постоянного тока поле вектора j не имеет источников.

Дифференциальная форма уравнения непрерывности. Преобразуем последние два уравнения к дифференциальной форме. Для этого представим заряд q как dV и правую часть (5.4) как

ddt dV t dV .

Здесь взят знак частной производной по времени, поскольку может зависеть не только от времени, но и от координат. Итак,

K j dS t dV .

Дальнейшее следует проделать так же, как это было сделано для потока вектора Е в § 1.4. В результате получим, что дивергенция вектора j в некоторой точке равна убыли плотности заряда в единицу времени в той же точке:

Отсюда вытекает условие стационарности (когда д /дt = 0):

Оно означает, что в случае постоянного тока поле вектора j не имеет источников.

§ 5.2. Закон Ома для однородного проводника

Закон Ома, открытый экспериментально, гласит: сила тока,

протекающего по однородному проводнику, пропорциональна разности потенциалов на его концах (напряжению U):

где R — электрическое сопротивление проводника. Единицей сопротивления служит ом (Ом).

Сопротивление R зависит от формы и размеров проводника, от его материала и температуры, а также — это следует помнить — от конфигурации (распределения) тока по проводнику. В случае провода смысл сопротивления не вызывает сомнений. В более общем случае объемного распределения тока уже нельзя говорить о сопротивлении, пока не указаны или расположение подводящих к интересующему нас проводнику проводов, или конфигурация тока.

В простейшем случае однородного цилиндрического проводника сопротивление

где l — длина проводника; S — площадь его поперечного сечения; — удельное электрическое сопротивление. Последнее зависит от материала проводника и его температуры. Выражают в ом-метрах (Oм•м).

Значения удельного электрического сопротивления для наиболее хороших проводников (медь, алюминий) составляют при комнатной температуре несколько единиц на 10–8 Oм•м.

Закон Ома в локальной форме. Найдем связь между плотностью тока j и полем Е в одной и той же точке проводящей среды. Ограничимся случаем изотропного проводника, в котором направления векторов j и Е совпадают.

Выделим мысленно в окрестности некоторой точки проводящей среды элементарный цилиндрический объем с образующими, параллельными вектору j, а значит, и вектору Е. Если поперечное сечение цилиндра dS, а его длина dl, то на основании (5.8) и (5.9) можно записать для такого элементарного ци-

dl/dS

ипосле соответствующих сокращений получим, уже в векторном виде,

где 1/ — удельная электропроводимость среды. Единицу, обратную ому, называют сименсом (См), поэтому единицейявляется сименс на метр (См/м).

Таким образом, соотношение (5.10) устанавливает связь между величинами, относящимися к одной и той же точке проводящей среды. Именно поэтому и говорят, что соотношение (5.10) выражает локальный закон Ома.

Способы вычисления сопротивления R. Существует несколько таких способов, и все они, в конечном счете, основаны на использовании соотношений (5.8) – (5.10). Целесообразность применения того или иного способа в каждом случае зависит от конкретной постановки задачи и от характера ее симметрии. Как это практически делается, показано на примерах задач 5.1–5.3 и 5.6.

О заряде внутри проводника с током. Если ток постоянный,

то избыточный заряд внутри однородного проводника всюду равен нулю. В самом деле, для постоянного тока справедливо уравнение (5.5). Перепишем его с учетом закона (5.10) в виде

K EdS 0,

где интеграл взят по произвольной замкнутой поверхности S внутри проводника. Для однородного проводника величину можно вынести из-под интеграла:

KEdS 0.

Оставшийся интеграл согласно теореме Гаусса пропорционален алгебраической сумме зарядов внутри замкнутой поверхности S, т. е. пропорционален избыточному заряду внутри этой

поверхности. Но из последнего равенства сразу видно, что этот интеграл равен нулю (ибо ; 0), а значит, равен нулю и избыточный заряд. В силу произвольности поверхности S мы заключаем, что избыточный заряд в этих условиях всюду внутри проводника равен нулю.

Избыточный заряд может появиться только на поверхности однородного проводника, в местах соприкосновения с другими проводниками, а также там, где проводник имеет неоднородности.

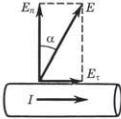
Электрическое поле проводника с током. Итак, при протекании тока на поверхности проводника (область неоднородности) выступает избыточный заряд, а это означает согласно (2.2), что снаружи проводника имеется нормальная составляющая вектора Е. Далее, из непрерывности тангенциальной составляющей вектора Е мы приходим к выводу о наличии и тангенциальной составляющей этого вектора вблизи поверхности проводника.

Таким образом, вектор Е вблизи поверхности проводника составляет (при наличии тока) с нормалью к ней некоторый не равный нулю угол (рис. 5.1).

И еще. Если токи стационарны, то распределение электрических зарядов в проводящей среде (вообще говоря, неоднородной) не меняется во времени, хотя и происходит движение зарядов: в каждой точке на место уходящих зарядов непрерывно поступают новые. Эти движущиеся заряды создают такое же кулоновское поле, что и неподвижные заряды той же конфигурации. Стало быть, электрическое поле стационарных токов — поле потенциальное.

Вместе с тем электрическое поле в случае стационарных токов существенно отличается от электростатического — кулоновского поля неподвижных зарядов. Последнее внутри проводников при равновесии зарядов равно нулю. Электрическое поле у стационарных токов есть также кулоновское поле, однако заряды, его возбуждающие, находятся в движении. Поэтому поле Е у стационарных токов существует и внутри проводников с током.