112 Глава 4

откуда поверхностная плотность силы

Мы получили интересный и важный результат, имеющий общий характер (в жидком или газообразном диэлектрике). Оказывается, поверхностная плотность силы, действующей на проводник, равна объемной плотности электрической энергии вблизи поверхности. Направлена эта сила всегда по нормали к поверхности, причем наружу проводника (стремясь его растянуть) независимо от знака поверхностного заряда.

Задачи

4.1.Энергия взаимодействия. Точечный заряд q находится на расстоянии l от безграничной проводящей плоскости. Найти энергию взаимодействия W этого заряда с зарядами, индуцированными на плоскости.

Решение. Мысленно «заморозим» распределенный по плоскости заряд, и в этих условиях переместим точечный заряд q в бесконечность. Заряд q при этом будет перемещаться в потенциальном поле, которое эквивалентно полю неподвижного точечного фиктивного заряда –q, расположенного на неизменном расстоянии l по другую сторону от плоскости. И мы сразу можем написать

4.2.Собственная, взаимная и полная энергии. Система состоит из

двух концентрических металлических оболочек радиусами R1 и R2 с соответствующими зарядами q1 и q2. Найти собственную энергию W1 и W2 каждой оболочки, энергию Wвз взаимодействия оболочек и полную электрическую энергию W данной системы, если

R2 > R1.

Решение. Собственная энергия каждой оболочки согласно (4.6) равна q /2, где — потенциал оболочки, обусловленный только

зарядом q на ней, т. е. q/4 0R, где R — радиус оболочки. Таким образом, собственная энергия каждой оболочки

Энергия же взаимодействия заряженных оболочек равна заряду q одной из них, умноженному на потенциал , который создает заряд другой оболочки в месте нахождения заряда q: Wвз = q .

В нашем случае (R2 > R1)

Полная электрическая энергия системы

4.3.Два небольших металлических шарика радиусами R1 и R2 находятся в вакууме на расстоянии, значительно превышающем их

размеры, и имеют некоторый определенный суммарный заряд.

При каком отношении q1/q2 зарядов на шариках электрическая энергия системы будет минимальной? Какова при этом разность

потенциалов между шариками?

Решение. Электрическая энергия данной системы

где W1 и W2 — собственные электрические энергии шариков (q /2); W12 — энергия их взаимодействия (q1 2 или q2 1); l — расстояние между шариками. Так как q2 = q – q1, где q — суммарный заряд системы, то

Энергия W будет минимальной при дW/дq1 = 0. Отсюда

где учтено, что R1 и R2 значительно меньше l. Таким образом

q1/q2 R1/R2.

Потенциал каждого шарика (их можно рассматривать как изолированные) T q/R, поэтому из предыдущего равенства следует, что 1 = 2, т. е. разность потенциалов при таком распределении равна нулю.

4.4.Локализация энергии в поле. Заряд q распределен равномерно по объему шара радиусом R. Полагая диэлектрическую проницаемость всюду равной единице, найти собственную электрическую

энергию шара и отношение энергии W1, локализованной внутри шара, к энергии W2 в окружающем пространстве.

Решение. Прежде всего найдем с помощью теоремы Гаусса поле внутри и вне шара:

Теперь вычислим собственную электрическую энергию шара:

Интересно, что отношение W1/W2 не зависит от радиуса шара.

4.5.Имеется сферическая оболочка, заряженная равномерно зарядом

q. В центре ее расположен точечный заряд q0. Найти работу электрических сил этой системы при расширении оболочки — увеличении ее радиуса от R1 до R2.

Решение. Работа электрических сил равна убыли электрической энергии системы:

A = W1 – W2.

Чтобы найти разность W1 – W2 , заметим, что при расширении оболочки (рис. 4.5) электрическое поле, а следовательно, и локализованная в нем энергия изменились только в заштрихованном сферическом слое. Значит,

где E1 и E2 — напряженность поля (в заштрихованном слое на расстоянии r от центра системы) до и после расширения оболочки. С помощью теоремы Гаусса находим

Замечание. Если эту работу искать через потенциал как А = q( 1 –

– 2), где — потенциал, создаваемый зарядом q0 в месте нахождения заряда q, ответ будет другим — неверным. Связано это с тем, что при таком подходе не учитывается та дополнительная работа, которую совершают электрические силы при изменении конфигурации заряда q на расширяющейся оболочке.

4.6.Точечный заряд q находится в центре сферического незаряженного проводящего слоя, внутренний и наружный радиусы которого равны соответственно а и b. Какую работу произведут электрические силы в данной системе,

если заряд q переместить из его первоначального положения через малое отверстие (рис. 4.6) на очень большое

Решение. Будем исходить из того, что работа электрических сил равна убыли электрической энергии системы. Последняя же, как известно, локализована в самом поле. Поэтому вопрос сводится, по существу, к выяснению, как изменится само поле в результате этого процесса.

Нетрудно сообразить, что поле вокруг заряда q изменится только

всферическом слое с внутренним и наружным радиусами а и b. В самом деле, в начальном положении заряда поля здесь не было, а

вконечном положении поле в этом слое есть (ведь сам сферический проводящий слой будет находиться далеко от заряда q). Следовательно, искомая работа

где Wсл — энергия, локализованная в сферическом слое. Имея в виду, что Е = q/4 0r2 и dV = 4 r2dr, получим после интегрирования

4.7.Работа при раздвижении пластин конденсатора. Имеется плоский воздушный конденсатор, площадь каждой обкладки которого равна S. Какую работу А против электрических сил надо совершить,

чтобы увеличить расстояние между обкладками от х1 до х2, если при этом поддерживать неизменным: 1) заряд конденсатора, рав-

ный q; 2) напряжение на конденсаторе, равное U? Чему равно приращение электрической энергии конденсатора в обоих случаях? Решение. 1. Искомая работа

где Е1 — напряженность поля, создаваемого одной обкладкой (E = /2 0). Именно в этом поле перемещается заряд, находящийся на другой обкладке. Данная работа целиком идет на приращение электрической энергии: W = A .

2. В этом случае сила, действующая на каждую обкладку конденсатора, будет зависеть от расстояния между ними. Запишем элементарную работу силы, действующей на обкладку при ее перемещении на dx относительно другой обкладки:

где учтено, что q = CU, E1 = U/2x и С = 0S/x. После интегрирования получим

Приращение электрической энергии конденсатора

Заметим, что W= –A

Таким образом, раздвигая обкладки, мы совершим положительную работу (против электрических сил), энергия же конденсатора при этом уменьшается. Чтобы понять, в чем тут дело, надо обратиться к источнику, поддерживающему неизменной разность потенциалов на конденсаторе. Этот источник тоже совершает работу Аист, причем согласно закону сохранения энергии Aист + А = W, откуда видно, что Aист = W – А = –2А < 0.

118 Глава 4

После подстановки (2) в (1) получим

Fx = 0( – 1) RU2/d.

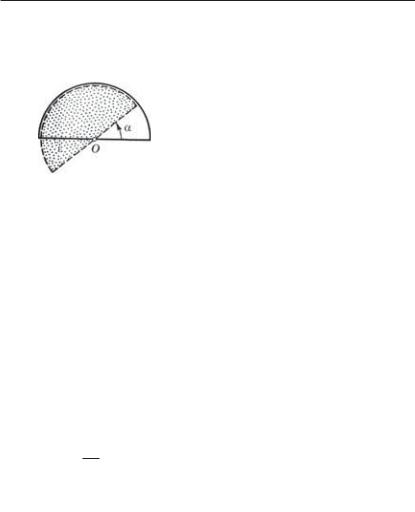
4.10. Конденсатор состоит из двух неподвижных пластин, имеющих форму полукруга радиусом R, и расположенной между ними подвижной пластины из диэлектрика с проницаемостью . Пластина может свободно поворачиваться вокруг оси О (рис. 4.7), ее толщина h, что практически равно расстоянию между неподвижными пластинами. Между пластинами конденсатора поддерживается постоянное напряжение U. Найти мо-

мент сил N относительно оси О, действующий на подвижную пластину в положении, показанном на рисунке.

Решение. Работа, которую совершает момент сил N при повороте пластины на элементарный угол d , равна убыли электрической энергии системы при q = const [см. (4.16)]:

В данном случае С = С1 + С , где С1 и С — емкости частей конденсатора без диэлектрика и с диэлектриком. Площадь сектора с углом определяется как S = R2/2, поэтому

C = 0 R2/2h + 0( )R2/2h.

Отсюда C (1 ). Подставим это выражение в формулу

2h

(1)и учтем, что С = q/U, тогда

Отрицательное значение Nz показывает, что момент этих сил действует по часовой стрелке (против положительного направления отсчета угла ; см. рис. 4.7). Этот момент стремится втянуть диэлектрик внутрь конденсатора.

Заметим, что Nz не зависит от угла . Однако в положении равновесия, когда = 0, момент Nz = 0. Это расхождение связано с тем, что при малых углах нельзя пренебрегать краевыми эффектами, как мы делали при решении этой задачи.