§ 11.1. Уравнение колебательного контура

Условие квазистационарности. Когда происходят электрические колебания, ток в цепи изменяется во времени и, вообще говоря, в каждый момент ток оказывается не одинаковым на разных участках цепи (из-за того что электромагнитные возмущения распространяются хотя и с очень большой, но конечной скоростью). Однако имеется много случаев, когда мгновенные значения тока оказываются практически одинаковыми на всех участках цепи (такой ток называют квазистационарным). Для этого все изменения во времени должны происходить настолько медленно, чтобы распространение электромагнитных возмущений можно было считать мгновенным. Если l — длина цепи, то на прохождение длины l электромагнитное возмущение затрачивает время порядка 0 l/с. Для периодически изменяющихся токов условие квазистационарности будет выполнено, если

0 l/c I T,

где Т — период изменений.

Например, для цепи длиной l 3 м время 0 10–8 с, и токи можно считать квазистационарными вплоть до частот 106 Гц (это соответствует Т 10–6 с).

В этой главе мы всюду будем предполагать, что в рассматриваемых нами случаях условие квазистационарности выполняется, и токи будем считать квазистационарными. Это позволит нам использовать формулы, полученные в статических полях. В частности, мы будем использовать тот факт, что мгновенные значения квазистационарных токов подчиняются закону Ома.

Колебательный контур. В цепи, содержащей катушку индуктивности L и конденсатор емкости С, могут возникнуть электрические колебания. Поэтому такую цепь называют колебательным контуром. Выясним, каким образом в колебательном контуре возникают и поддерживаются электрические колебания.

Пусть вначале верхняя обкладка конденсатора заряжена положительно, а нижняя отрицательно (рис. 11.1, а). При этом вся энергия колебательного контура сосредоточена в конденсаторе. Замкнем ключ

K. Конденсатор начнет разря-

жаться, и через катушку L потечет ток. Электрическая энергия конденсатора начнет

превращаться в магнитную энергию катушки. Этот процесс закончится, когда конденсатор полностью разрядится, а ток в цепи достигнет максимума (рис. 11.1, б). С этого момента ток, не меняя направления, начнет убывать. Однако он прекратится не сразу — его будет поддерживать э.д.с. самоиндукции. Ток будет перезаряжать конденсатор, возникнет электрическое поле, стремящееся ослабить ток. Наконец, ток прекратится, а заряд на конденсаторе достигнет максимума. С этого момента конденсатор начнет разряжаться опять, ток потечет в обратном направлении и т. д. — процесс будет повторяться.

В контуре при отсутствии сопротивления проводников будут совершаться строго периодические колебания. В ходе процесса периодически изменяются заряд на обкладках конденсатора, напряжение на нем и ток через катушку. Колебания сопровождаются взаимными превращениями энергии электрического и магнитного полей.

Если же сопротивление проводников R ; 0, то помимо описанного процесса будет происходить преобразование электромагнитной энергии в джоулеву теплоту.

Сопротивление проводников цепи R принято называть активным сопротивлением.

Уравнение колебательного контура.

Найдем уравнение колебаний в контуре, содержащем последовательно соединенные конденсатор С, катушку индуктивности L, активное сопротивление R и внешнюю переменную э.д.с. (рис. 11.2).

Прежде всего выберем положительное направление обхода контура, например по часовой стрелке. Рассмотрим ситуацию в момент времени, когда нижняя обкладка 2 в процессе перезарядки конденсатора имеет некоторый заряд q > 0 и ток I течет в положительным направлении. Тогда за промежуток времени dt заряд q получит приращение dq > 0, и ток в контуре определяется как

Следовательно, если I > 0, то и dq > 0, и наоборот (знак I совпадает со знаком dq).

Согласно закону Ома для участка цепи 1RL2

(знак q должен совпадать со знаком разности 2 – 1, ибо С > 0). Поэтому уравнение (11.2) можно переписать в виде

Это и есть уравнение колебательного контура — линейное дифференциальное неоднородное уравнение второго порядка с постоянными коэффициентами. Найдя с помощью этого уравнения q(t), мы можем легко вычислить напряжение на конденсаторе как UC 2 – 1 q/C и силу тока I — по формуле (11.1).

292 Глава 11

где qт — амплитудное значение заряда на обкладке конденсатора, 0 — собственная частота контура, — начальная фаза. Значение 0 определяется только свойствами самого контура, значения же qm и — начальными условиями. В качестве та.- ковых можно взять, например, значения заряда q и тока I q в момент t 0.

Согласно (11.6) 0 1/LC, поэтому период свободных неза-

(формула Томсона).

Найдя ток I (дифференцированием (11.8) по времени) и имея в виду, что напряжение на конденсаторе находится в фазе с зарядом q, нетрудно убедиться, что при свободных незатухающих колебаниях ток I опережает по фазе напряжение на конденсаторе на /2.

Свободные затухающие колебания. Каждый реальный контур обладает активным сопротивлением, и энергия, запасенная в контуре, постепенно расходуется на нагревание. Свободные колебания будут затухающими.

Уравнение данного колебательного контура мы получим, по-

Можно показать (но мы не будем этого делать, поскольку нас интересует другая сторона вопроса), что при = < 0 решение этого однородного дифференциального уравнения имеет вид

Величину Т 2 / называют тем не менее периодом зату-

где Т0 — период свободных незатухающих колебаний. Множитель qme–=t в (11.11) называют амплитудой затуха-

ющих колебаний. Зависимость ее от времени показана штриховой линией на рис. 11.3.

Напряжение на конденсаторе и ток в контуре. Зная q(t), можно найти напряжение на конденсаторе и ток в контуре. Напряжение на конденсаторе

Ток в контуре

Idq qme =t [ =cos( t ) sin( t )] . dt

Преобразуем выражение в квадратных скобках к косинусу. Для этого умножим и разделим это выражение на 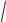2 =2 0 , а затем введем угол по формулам

( /2 < < ). Это означает, что при наличии активного сопротивления R ток в контуре опережает по фазе напряжение (11.14) на конденсаторе более чем на /2. Заметим, что при R 0 опережение /2.

Графики зависимостей UC(t) и I(t) имеют вид, аналогичный показанному на рис. 11.3 для q(t).

Пример. Колебательный контур содержит конденсатор емкости С и катушку с активным сопротивлением R и индуктивностью L. Найдем отношение энергии магнитного поля к энергии электрического поля в контуре в момент максимума тока.

294 Глава 11

Согласно уравнению колебательного контура (11.3)

L dI RI q 0. dt C

В момент максимума тока dI/dt = 0 и RI = – q/C. Поэтому искомое отношение

Величины, характеризующие затухание.

1. Коэффициент затухания = и время релаксации 0 —

время, за которое амплитуда колебаний уменьшается в е раз. Из формулы (11.11) нетрудно видеть, что

2. Логарифмический декремент затухания . Он определяется как натуральный логарифм отношения двух значений амплитуд, взятых через период колебания Т:

a(t T )

где а — амплитуда соответствующей величины (q, U, I). Или иначе:

где Ne — число колебаний за время 0, т. е. за время, в течение которого амплитуда колебаний уменьшается в е раз. Это легко получить из формул (11.17) и (11.18).

где — логарифмический декремент затухания. Чем меньше затухание, тем больше Q. При слабом затухании (= I 0) согласно (11.20) добротность

И еще одна полезная формула для Q в случае слабого затухания

где W — энергия, запасенная в контуре, W — уменьшение этой энергии за период колебания Т. В самом деле, энергия W пропорциональна квадрату амплитуды заряда конденсатора, т. е. W T е–2=t. Отсюда относительное уменьшение энергии за период W/W 2=T 2 . Остается учесть согласно (11.21), что

/Q.

Взаключение отметим, что при = j 0 вместо колебаний будет происходить апериодический разряд конденсатора. Актив-

ное сопротивление контура, при котором наступает апериодический процесс, называют критическим:

Рассмотрим два примера.

Пример 1. Колебательный контур имеет емкость С, индуктивность L и активное сопротивление R. Найдем, через сколько колебаний амплитуда тока в этом контуре уменьшится в е раз.

Амплитуда тока (Im T е–=t) уменьшится в е раз за время 0 1/=. За это время совершится Ne колебаний. Если Т — период затухающих колебаний, то

Пример 2. Найдем время, за которое амплитуда колебаний тока в контуре с добротностью Q уменьшится в , раз, если частота затухающих колебаний равна .

Так как амплитуда тока Im T е–=t, то время t0, за которое амплитуда уменьшится в , раз, определяется уравнением , = еxp(=t0). Отсюда

t0 (ln,)/=.