
- •Содержание
- •Предисловие к 4-му изданию
- •Принятые обозначения
- •§ 1.1. Электрическое поле
- •§ 1.2. Теорема Гаусса
- •§ 1.3. Применения теоремы Гаусса
- •§ 1.4. Теорема Гаусса в дифференциальной форме
- •§ 1.5. Циркуляция вектора Е. Потенциал
- •§ 1.6. Связь между потенциалом и вектором Е
- •§ 1.7. Электрический диполь
- •Задачи
- •§ 2.1. Поле в веществе
- •§ 2.2. Поле внутри и снаружи проводника
- •§ 2.3. Силы, действующие на поверхность проводника
- •§ 2.4. Свойства замкнутой проводящей оболочки
- •§ 2.6. Электроемкость. Конденсаторы
- •Задачи
- •§ 3.1. Поляризация диэлектрика
- •§ 3.2. Поляризованность Р
- •§ 3.3. Свойства поля вектора Р
- •§ 3.4. Вектор D
- •§ 3.5. Условия на границе
- •§ 3.6. Поле в однородном диэлектрике
- •Задачи
- •§ 4.1. Электрическая энергия системы зарядов
- •§ 4.3. Энергия электрического поля
- •§ 4.4. Система двух заряженных тел
- •§ 4.5. Силы при наличии диэлектрика
- •Задачи
- •§ 5.1. Плотность тока. Уравнение непрерывности
- •§ 5.2. Закон Ома для однородного проводника
- •§ 5.3. Обобщенный закон Ома
- •§ 5.4. Разветвленные цепи. Правила Кирхгофа
- •§ 5.5. Закон Джоуля–Ленца
- •Задачи
- •§ 6.1. Сила Лоренца. Поле В
- •§ 6.2. Закон Био–Савара
- •§ 6.3. Основные законы магнитного поля
- •§ 6.5. Дифференциальная форма основных законов магнитного поля
- •§ 6.6. Сила Ампера
- •§ 6.8. Работа при перемещении контура с током
- •Задачи
- •§ 7.1. Намагничение вещества. Намагниченность J
- •§ 7.2. Циркуляция вектора J
- •§ 7.3. Вектор Н
- •§ 7.4. Граничные условия для В и Н
- •§ 7.5. Поле в однородном магнетике
- •§ 7.6. Ферромагнетизм
- •Задачи
- •§ 8.1. Электромагнитное поле. Инвариантность заряда
- •§ 8.2. Законы преобразования полей Е и В
- •§ 8.3. Следствия из законов преобразования полей
- •§ 8.4. Инварианты электромагнитного поля
- •Задачи
- •§ 9.1. Закон электромагнитной индукции. Правило Ленца
- •§ 9.2. Природа электромагнитной индукции
- •§ 9.3. Явление самоиндукции
- •§ 9.4. Взаимная индукция
- •§ 9.5. Энергия магнитного поля
- •§ 9.6. Магнитная энергия двух контуров с токами
- •§ 9.7. Энергия и силы в магнитном поле
- •Задачи
- •§ 10.1. Ток смещения
- •§ 10.2. Система уравнений Максвелла
- •§ 10.3. Свойства уравнений Максвелла
- •§ 10.4. Энергия и поток энергии. Вектор Пойнтинга
- •§ 10.5. Импульс электромагнитного поля
- •Задачи
- •§ 11.1. Уравнение колебательного контура
- •§ 11.2. Свободные электрические колебания
- •§ 11.3. Вынужденные электрические колебания
- •§ 11.4. Переменный ток
- •Задачи
- •1. Единицы величин в СИ и системе Гаусса
- •3. Основные величины и единицы СИ
- •4. Греческий алфавит
- •5. Некоторые физические константы
- •Предметный указатель

102 |
Глава 4 |
|
|
§4.3. Энергия электрического поля
Олокализации энергии. Формула (4.4) определяет электрическую энергию W любой системы через заряды и потенциалы. Но, оказывается, энергию W можно выразить также и через величину, характеризующую само электрическое поле, — через напряженность Е. Убедимся в этом сначала на простейшем примере плоского конденсатора, пренебрегая искажением поля
украев пластин (краевым эффектом). Подстановка в формулу W CU2/2 выражения С 0S/h дает
W |
CU2 |
|
|
0 |
SU2 |
|
|
0 |
U 2 |
|||
|
|
|
|
|
|
! |
|
|
Sh. |
|||
2 |
|
2h |
|
|
|
|||||||
|
|
|
2 |
|
h # |
|
||||||
А поскольку U/h Е и Sh V (объем между обкладками конденсатора), то
W ( |
E2/2)V (ED/2)V. |
(4.8) |
0 |
|
|
Полученная формула справедлива для однородного поля, заполняющего объем V.
В общей теории доказывается, что в случае неоднородного поля энергия W для изотропных диэлектриков определяется формулой
W |
|
|
0 E2 |
dV |
|
ED |
dV. |
(4.9) |
|
|
2 |
2 |
|
||||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
Подынтегральное выражение в этом уравнении имеет смысл энергии, заключенной в объеме dV. Это подводит нас к весьма важной и плодотворной физической идее о локализации энергии в самом поле. Данное предположение нашло опытное подтверждение в области переменных во времени полей. Только там встречаются явления, которые можно истолковать на основе идеи о локализации энергии в поле. Именно переменные поля могут существовать независимо от возбудивших их электрических зарядов и распространяться в пространстве в виде электромагнитных волн. И опыт показывает, что электромагнитные волны переносят энергию — уже это заставляет нас признать, что носителем энергии является само поле.
Энергия электрического поля |
103 |
|
|
Из последних двух формул следует, что электрическая энергия распределена в пространстве с объемной плотностью
w |
|
0 E2 |
|
ED |
. |
(4.10) |
|
|
2 |
2 |
|
||||
|
|
|
|
|
|
||
Заметим, что эта формула справедлива только в случае изотропного диэлектрика, для которого выполняется соотношение D 0Е. Для анизотропных диэлектриков дело обстоит сложнее.
Еще об обосновании формулы (4.9). Энергия уединенного заряженного проводника, как известно, есть W = q /2. Покажем, что это так, исходя из идеи о локализации энергии в поле.
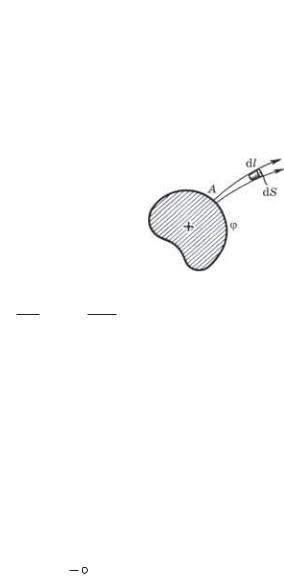
Рассмотрим произвольный положительно заряженный проводник. Выделим мысленно бесконечно малого сечения трубку, ограниченную линиями вектора Е (рис. 4.2), и в ней возьмем элементарный объем dV= dSdl. В этом объеме заключена энергия
ED dS dl DdS E dl.
22
Теперь найдем энергию, локализованную во всей выделенной нами трубке. Для этого проинтегрируем последнее выражение, учитывая, что произведение D dS одинаково во всех сечениях трубки, и поэтому его можно вынести за знак интеграла:
|
D dS |
% |
D dS |
|
|
dW |
E dl |
, |
|||
|
2 |
||||
2 |
A |
|
|||
|
|
|
|
||
где A — начало трубки.
Остается сделать последний шаг — проинтегрировать полученное выражение по всем трубкам, и мы найдем энергию, локализованную во всем поле. Принимая во внимание, что потенциал одинаков у торцов всех трубок (они ведь начинаются на поверхности проводника), запишем
W 2 DdS ,

104 |
Глава 4 |
|
|
где интегрирование проводится по замкнутой поверхности, совпадающей с одной из эквипотенциальных поверхностей. По теореме Гаусса этот интеграл равен заряду q на проводнике, и мы получим окончательно
W q /2,
что и требовалось доказать.
Рассмотрим два примера, иллюстрирующих возможности и преимущества, которые дает использование идеи о локализации энергии в поле.
Пример 1. Точечный заряд q находится в центре шарового слоя из однородного диэлектрика с проницаемостью . Внутренний и наружный радиусы слоя равны соответственно а и b. Найдем электрическую энергию, заключенную в данном диэлектрическом слое.
Мысленно выделим в диэлектрике очень тонкий концентрический сферический слой радиусом от r до r + dr. Энергия, локализованная в этом слое:
dW 0 E2 4 r 2 dr ,
2
где Е = q2/4 0 r2. Проинтегрировав предыдущее выражение по r от а до b, получим
|
|
q |
2 |
|
|
1 |
|
1 |
|
W |
|
|
|
||||||
|
|
|
! |
|
|||||
|
|
|
|
|
|||||
|
|
! |
a |
. |
|||||
|
8 |
|
|
b |
# |
||||
|
|
|
0 |
|
|
|
|
|
|
Пример 2. Найдем работу, которую надо совершить против электрических сил, чтобы удалить диэлектрическую пластинку из плоского заряженного конденсатора. Предполагается, что заряд q конденсатора остается неизменным и диэлектрик заполняет все пространство между обкладками. Емкость конденсатора без диэлектрика равна С.
Работа против электрических сил в этой системе пойдет на приращение ее электрической энергии:
A W W2 – W1,
где W1 — энергия поля между обкладками конденсатора при наличии диэлектрика; W2 — то же, но при отсутствии диэлектрика. Имея в виду, что модуль вектора D не изме-

Энергия электрического поля |
|
|
|
|
|
|
|
|
|
105 |
||
|
||||||||||||
нится в результате извлечения пластины, т. е. D2 = D1 = , |
||||||||||||
запишем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D 2 |
|
D 2 |
|
q 2 |
|
1 |
|
|
A W W ! |
|
|
|
V |
|
!1 |
|
|
, |
|||
2 |
|
|
|
|||||||||
|
2 |
1 |
! |
2 |
|
2C ! |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
0 |
0 |
# |
|
|
|
|
# |
|
где V Sh и С 0S/h; S и h — площадь каждой обкладки и расстояние между ними.
Работа поля при поляризации диэлектрика. Анализируя формулу (4.10) для объемной плотности энергии, мы замечаем, что при одном и том же значении E величина w при наличии диэлектрика оказывается в раз больше, чем при отсутствии диэлектрика. На первый взгляд это кажется странным: ведь напряженность поля в обоих случаях мы поддерживаем одной и той же. Как мы сейчас увидим, все дело в том, что при создании поля в диэлектрике оно совершает дополнительную работу, связанную с поляризацией. И под энергией поля в диэлектрике следует понимать всю энергию, которую нужно затратить на возбуждение электрического поля, а она складывается из собственной электрической энергии и той дополнительной работы, которая совершается при поляризации диэлектрика.
Чтобы в этом убедиться, подставим в (4.10) вместо D величину 0E + Р, тогда
w |
|
0 E2 |
|
EP |
|
(4.11) |
|
|
|
|
|
. |
|||
22
Первое слагаемое здесь совпадает с плотностью энергии поля Е в вакууме. Остается проверить, что «дополнительная» энергия ЕР/2 связана с поляризацией диэлектрика.
Подсчитаем работу, которую совершает электрическое поле на поляризацию единицы объема диэлектрика, т. е. на смещение зарядов и соответственно по и против поля — при возрастании напряженности от Е до Е + dE. Пренебрегая членами второго порядка малости, запишем
A Edl Edl ,
где dl+ и dl– — дополнительные смещения при увеличении поля на dE (рис. 4.3). Учитывая, что , получаем
A (dl dl )E dl)E ,
