
- •Содержание
- •Предисловие к 4-му изданию
- •Принятые обозначения
- •§ 1.1. Электрическое поле
- •§ 1.2. Теорема Гаусса
- •§ 1.3. Применения теоремы Гаусса
- •§ 1.4. Теорема Гаусса в дифференциальной форме
- •§ 1.5. Циркуляция вектора Е. Потенциал
- •§ 1.6. Связь между потенциалом и вектором Е
- •§ 1.7. Электрический диполь
- •Задачи
- •§ 2.1. Поле в веществе
- •§ 2.2. Поле внутри и снаружи проводника
- •§ 2.3. Силы, действующие на поверхность проводника
- •§ 2.4. Свойства замкнутой проводящей оболочки
- •§ 2.6. Электроемкость. Конденсаторы
- •Задачи
- •§ 3.1. Поляризация диэлектрика
- •§ 3.2. Поляризованность Р
- •§ 3.3. Свойства поля вектора Р
- •§ 3.4. Вектор D
- •§ 3.5. Условия на границе
- •§ 3.6. Поле в однородном диэлектрике
- •Задачи
- •§ 4.1. Электрическая энергия системы зарядов
- •§ 4.3. Энергия электрического поля
- •§ 4.4. Система двух заряженных тел
- •§ 4.5. Силы при наличии диэлектрика
- •Задачи
- •§ 5.1. Плотность тока. Уравнение непрерывности
- •§ 5.2. Закон Ома для однородного проводника
- •§ 5.3. Обобщенный закон Ома
- •§ 5.4. Разветвленные цепи. Правила Кирхгофа
- •§ 5.5. Закон Джоуля–Ленца
- •Задачи
- •§ 6.1. Сила Лоренца. Поле В
- •§ 6.2. Закон Био–Савара
- •§ 6.3. Основные законы магнитного поля
- •§ 6.5. Дифференциальная форма основных законов магнитного поля
- •§ 6.6. Сила Ампера
- •§ 6.8. Работа при перемещении контура с током
- •Задачи
- •§ 7.1. Намагничение вещества. Намагниченность J
- •§ 7.2. Циркуляция вектора J
- •§ 7.3. Вектор Н
- •§ 7.4. Граничные условия для В и Н
- •§ 7.5. Поле в однородном магнетике
- •§ 7.6. Ферромагнетизм
- •Задачи
- •§ 8.1. Электромагнитное поле. Инвариантность заряда
- •§ 8.2. Законы преобразования полей Е и В
- •§ 8.3. Следствия из законов преобразования полей
- •§ 8.4. Инварианты электромагнитного поля
- •Задачи
- •§ 9.1. Закон электромагнитной индукции. Правило Ленца
- •§ 9.2. Природа электромагнитной индукции
- •§ 9.3. Явление самоиндукции
- •§ 9.4. Взаимная индукция
- •§ 9.5. Энергия магнитного поля
- •§ 9.6. Магнитная энергия двух контуров с токами
- •§ 9.7. Энергия и силы в магнитном поле
- •Задачи
- •§ 10.1. Ток смещения
- •§ 10.2. Система уравнений Максвелла
- •§ 10.3. Свойства уравнений Максвелла
- •§ 10.4. Энергия и поток энергии. Вектор Пойнтинга
- •§ 10.5. Импульс электромагнитного поля
- •Задачи
- •§ 11.1. Уравнение колебательного контура
- •§ 11.2. Свободные электрические колебания
- •§ 11.3. Вынужденные электрические колебания
- •§ 11.4. Переменный ток
- •Задачи
- •1. Единицы величин в СИ и системе Гаусса
- •3. Основные величины и единицы СИ
- •4. Греческий алфавит
- •5. Некоторые физические константы
- •Предметный указатель

§ 4.1. Электрическая энергия системы зарядов
Энергетический подход к взаимодействию. Такой подход к взаимодействию электрических зарядов является, как мы увидим, весьма плодотворным по своим практическим применениям, а кроме того, открывает возможность по-иному взглянуть и на само электрическое поле как физическую реальность.
Прежде всего мы выясним, как можно прийти к понятию о энергии взаимодействия системы зарядов.
1. Сначала рассмотрим систему, состоящую из двух точечных зарядов 1 и 2. Найдем алгебраическую сумму элементарных работ сил F1 и F2, с которыми эти заряды взаимодействуют. Пусть в некоторой K-системе отсчета за время dt заряды совершили перемещения dl1 и dl2. Тогда работа этих сил
A1,2 = F1dl1 F2 dl2 .
Учитывая, что F2 = –F1 (по третьему закону Ньютона), перепишем предыдущее выражение:
A1,2 = F1 (dl1 dl2 ) .
Величина в скобках — это перемещение заряда 1 относительно заряда 2. Точнее, это есть перемещение заряда 1 в K -сис- теме отсчета, жестко связанной с зарядом 2 и перемещающейся вместе с ним поступательно по отношению к исходной K-систе- ме. Действительно, перемещение dl1 заряда 1 в K-системе может быть представлено как перемещение dl2 K -системы плюс перемещение dl1 заряда 1 относительно этой K -системы: dl1 = dl2 + dl1 . Отсюда dl1 dl2 = dl1 и
A1,2 = F1dl1 .
Энергия электрического поля |
97 |
|
|
Итак, оказывается, что сумма элементарных работ в произвольной K-системе отсчета всегда равна элементарной работе, которую совершает сила, действующая на один заряд, в системе отсчета, где другой заряд покоится. Иначе говоря, работаА1,2 не зависит от выбора исходной K-системы отсчета.
Сила F1, действующая на заряд 1 со стороны заряда 2, консервативная (как сила центральная). Поэтому работа данной силы на перемещении dl1 может быть представлена как убыль потенциальной энергии заряда 1 в поле заряда 2 или как убыль потенциальной энергии взаимодействия этой пары зарядов:
A1,2 –dW12,
где W12 — величина, зависящая только от расстояния между данными зарядами.
2. Теперь перейдем к системе из трех точечных зарядов (полученный для этого случая результат легко будет обобщить на систему из произвольного числа зарядов). Работа, которую совершают все силы взаимодействия при элементарных перемещениях всех зарядов, может быть представлена как сумма работ
всех трех пар взаимодействий, т. е. A A1,2 A1,3 A2,3. Но для каждой пары взаимодействий, как только что было показа-
но, Ai,k –dWik, поэтому
A –d(W12 + W13 + W23) –dW,
где W — энергия взаимодействия данной системы зарядов,
W W12 + W13 + W23.
Каждое слагаемое этой суммы зависит от расстояния между соответствующими зарядами, поэтому энергия W данной системы зарядов есть функция ее конфигурации.
Подобные рассуждения, очевидно, справедливы и для системы из любого числа зарядов. Значит, можно утверждать, что каждой конфигурации произвольной системы зарядов присуще свое значение энергии W, и работа всех сил взаимодействия при изменении этой конфигурации равна убыли W:
A –dW. |
(4.1) |
98 |
Глава 4 |
|
|
Энергия взаимодействия. Найдем выражение для энергии W. Сначала рассмотрим опять систему из трех точечных зарядов, для которой мы показали, что W W12 + W13 + W23. Преобразуем эту сумму следующим образом. Представим каждое слагаемое Wik в симметричном виде: Wik (Wik + Wki)/2, поскольку Wik Wki . Тогда
W (W12 + W21 + W13 + W31 + W23 + W32)/2.
Сгруппируем члены с одинаковыми первыми индексами:
W [(W12 + W13) + (W21 + W23) + (W31 + W32)]/2.
Каждая сумма в круглых скобках — это энергия Wi взаимодействия i-го заряда с остальными зарядами. Поэтому последнее выражение можно переписать так:
3
W 1/2 (W1 W2 W3 ) 1/2 Wi . i 1
Обобщение полученного выражения на систему из произвольного числа зарядов очевидно, ибо ясно, что проведенные рассуждения совершенно не зависят от числа зарядов, составляющих систему. Итак, энергия взаимодействия системы точечных зарядов
W 1/2 Wi . |
(4.2) |
Имея в виду, что Wi qi i, где qi — i-й заряд системы; i — потенциал, создаваемый в месте нахождения i-го заряда всеми остальными зарядами системы, получим окончательное выражение для энергии взаимодействия системы точечных зарядов:
W 1/2 q i i . |
(4.3) |
Пример. Четыре одинаковых точечных заряда q находятся в вершинах тетраэдра с ребром а (рис. 4.1). Найдем энергию взаимодействия зарядов этой системы.
Энергия взаимодействия каждой пары зарядов здесь одинакова и равна W1 = q2/4 0а. Всего таких взаимодействующих пар, как видно из рисунка, шесть, поэтому энергия взаимо-
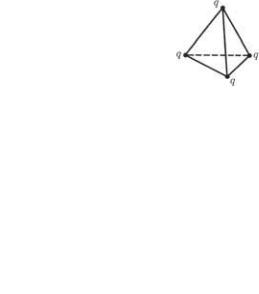
Энергия электрического поля |
99 |
|
|
действия всех точечных зарядов данной системы
W 6W |
1 |
6q2/4 a. |
|
|
|
|
|
|
|||||
|
|
|
|
|
0 |
|
|
|
|
|
|
||
Иной подход к решению этого вопроса |
|
||||||||||||
основан на использовании формулы (4.3). |
|
||||||||||||
Потенциал в месте нахождения одного из |
Рис. 4.1 |
||||||||||||
зарядов, обусловленный полем всех осталь- |
|||||||||||||
|
|||||||||||||
ных зарядов, равен 3q/4 0a. Поэтому |
|
||||||||||||
W 1/ |
4 |
|
|
|
1/ 4q |
1 |
|
6q |
2 |
|
|
||
q |
|
|
|
|
|
|
|
||||||
i |
i |
|
|
|
|
. |
|||||||
|
2 |
i 1 |
|
2 |
4 0 |
|
a |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||
Полная энергия взаимодействия. Если заряды распределены непрерывно, то, разлагая систему зарядов на совокупность элементарных зарядов dq dV и переходя от суммирования в (4.3) к интегрированию, получаем
W 1/2 dV, |
(4.4) |
|
|
где — потенциал, создаваемый всеми зарядами системы в элементе объемом dV. Аналогичное выражение можно записать для распределения зарядов, например, по поверхности; для этого достаточно в формуле (4.4) заменить на и dV на dS.
Можно ошибочно подумать (и это часто приводит к недоразумениям), что выражение (4.4) — это только видоизмененное выражение (4.3), соответствующее замене представления о точечных зарядах представлением о непрерывно распределенном заряде. В действительности это не так — оба выражения отличаются по своему содержанию. Происхождение этого различия — в разном смысле потенциала , входящего в оба выражения, что лучше всего пояснить на следующем примере.
Пусть система состоит из двух шариков, имеющих заряды q1 и q2. Расстояние между шариками значительно больше их размеров, поэтому заряды q1 и q2 можно считать точечными. Найдем энергию W данной системы с помощью обеих формул.
Согласно формуле (4.3)
W (q1 1 + q2 2)/2 q1 1 q2 2,

100 |
Глава 4 |
|
|
где 1 — потенциал, создаваемый зарядом q2 в месте нахождения заряда q1; аналогичный смысл имеет и потенциал 2.
Согласно же формуле (4.4) мы должны разбить заряд каждого шарика на бесконечно малые элементы dV и каждый из них умножить на потенциал , создаваемый не только зарядами другого шарика, но и элементами заряда этого шарика. Ясно, что результат будет совершенно другим, а именно:
W W1 + W2 + W12, |
(4.5) |
где W1 — энергия взаимодействия друг с другом элементов заряда первого шарика; W2 — то же, но для второго шарика; W12 — энергия взаимодействия элементов заряда первого шарика с элементами заряда второго шарика. Энергии W1 и W2
называют собственными энергиями зарядов q1 и q2, a W12 — энергией взаимодействия заряда q1 с зарядом q2.
Таким образом, мы видим, что расчет энергии W по формуле (4.3) дает только W12, а расчет по формуле (4.4) — полную энергию взаимодействия: кроме W12 еще и собственные энергии W1 и W2. Игнорирование этого обстоятельства зачастую является источником грубых ошибок.
К данному вопросу мы еще вернемся в § 4.4, а сейчас получим с помощью формулы (4.4) несколько важных результатов.
§4.2. Энергия заряженных проводника
иконденсатора
Энергия уединенного проводника. Пусть проводник имеет заряд q и потенциал . Поскольку значение во всех точках, где имеется заряд, одинаково, можно вынести из-под знака интеграла в формуле (4.4). Тогда оставшийся интеграл есть не что иное, как заряд q на проводнике, и
W |
q |
|
C 2 |
|
q 2 |
. |
(4.6) |
2 |
2 |
|
2C |
||||
|
|
||||||
Эти три выражения написаны с учетом того, что С = q/ . Энергия конденсатора. Пусть q и + — заряд и потенциал
положительно заряженной обкладки конденсатора. Согласно формуле (4.4) интеграл можно разбить на две части — для од-

Энергия электрического поля |
101 |
|
|
ной и другой обкладок. Тогда
W (q+ + + q– –)/2.
Так как q– –q+ , то
W q+( + – –)/2 qU/2,
где q q+ — заряд конденсатора, U — разность потенциалов на его обкладках. Приняв во внимание, что С q/U, получим следующие выражения для энергии конденсатора:
W |
qU |
|
CU2 |
|
q 2 |
(4.7) |
|
|
|
|
. |
||||
2 |
|
2 |
|
2C |
|||
|
|
|
|||||
Здесь надо заметить, что эти формулы определяют полную энергию взаимодействия: не только энергию взаимодействия зарядов одной обкладки с зарядами другой, но и энергию взаимодействия зарядов внутри каждой обкладки.
А если есть диэлектрик? Мы сейчас убедимся, что формулы
(4.6) и (4.7) справедливы и при наличии диэлектрика. С этой целью рассмотрим процесс зарядки конденсатора как перенос заряда малыми порциями dq с одной обкладки на другую.
Элементарная работа, совершенная нами при этом против сил поля, запишется как
A U dq (q /C)dq ,
где U — разность потенциалов между обкладками в момент, когда переносится очередная порция заряда dq .
Проинтегрировав это выражение по q от 0 до q, получим
A q2/2C,
что совпадает с выражением для полной энергии конденсатора. Значит, совершаемая нами работа против сил электрического поля целиком идет на создание энергии W заряженного конденсатора. Кроме того, полученное выражение для работы А справедливо и в том случае, когда между обкладками конденсатора имеется произвольный диэлектрик. Этим самым мы доказали справедливость формул (4.7) и при наличии диэлектрика.
Все сказанное относится, очевидно, и к формулам (4.6).
