(при котором рm B) и, кроме того, под действием результирующей силы F втягиваться туда, где индукция В больше.

§ 6.8. Работа при перемещении контура с током

Когда контур с током находится во внешнем магнитном поле — мы будем предполагать, что оно постоянное, — на отдельные элементы контура действуют амперовы силы, а поэтому при перемещении контура эти силы будут совершать работу. В этом параграфе мы покажем, что работа, которую совершают амперовы силы при элементарном перемещении контура с током I, определяется как

где dФ — приращение магнитного потока сквозь контур при данном перемещении.

Доказательство этой формулы проведем в три этапа.

1. Сначала рассмотрим частный случай: контур (рис. 6.15) с подвижной перемычкой длины l находится в однородном магнитном поле, перпендикулярном плоскости контура и направленном за плоскость рисунка. На перемычку согласно (6.29) действует амперова сила F = IlВ. При перемещении перемычки вправо на dx эта сила совершает положительную работу

где dS — приращение площади, ограниченной контуром. Для определения знака магнитного потока Ф условимся всегда брать нормаль n к поверхности, ограниченной контуром, так, чтобы она образовывала с направлением тока в контуре правовинтовую систему

(см. рис. 6.15). При этом ток I будет всегда величиной положительной. Поток же Ф может быть как положительным, так и отрицательным. Но в нашем случае как Ф, так и dФ = В dS являются ве-

личинами положительными (если бы поле В было направлено на нас или перемычка перемещалась бы влево, то в обоих случаях dФ < 0). Как бы то ни было, в любом из этих случаев выражение (6.38) можно представить в виде (6.37).

2.Полученный результат справедлив и для произвольного направления поля В. Чтобы убедиться в этом, разложим вектор

Вна три составляющие: В = Вn + Вl + Вx. Составляющая Вl — вдоль перемычки — параллельна току в ней и поэтому не оказывает на перемычку силового действия. Составляющая Вx — вдоль перемещения — дает силу, перпендикулярную переме-

щению, работы она не совершает. Остается лишь составляющая Вn — перпендикулярная плоскости, в которой перемещается перемычка. Поэтому в формуле (6.38) вместо В надо брать

только Bn. Но BndS = dФ, и мы опять приходим к формуле (6.37).

3.Теперь перейдем к рассмотрению любого контура при произвольном перемещении его в постоянном неоднородном магнитном поле (контур может при этом и произвольным образом деформироваться). Разобъем мысленно данный контур на бесконечно малые элементы тока и рассмотрим бесконечно малые перемещения их. В этих условиях магнитное поле, в котором перемещается каждый элемент тока, можно считать однородным. Для такого перемещения к каждому элементу тока при-

менимо выражение dА = Id Ф для элементарной работы, где под d Ф надо понимать вклад в приращение потока сквозь контур от данного элемента контура. Сложив такие элементарные работы для всех элементов контура, снова получим выражение (6.37), где dФ есть приращение магнитного потока сквозь весь контур.

Чтобы найти работу амперовых сил при полном перемещении контура с током от начального положения 1 до конечного 2, достаточно проинтегрировать выражение (6.37):

где Ф1 и Ф2 — магнитные потоки сквозь контур в начальном и конечном положениях. Таким образом, работа амперовых сил в этом случае равна произведению силы тока на приращение магнитного потока сквозь контур. Выражение (6.40) дает не только величину, но и знак совершаемой работы.

Пример. Плоский контур с током I поворачивают в магнитном поле В из положения, при котором нормаль к контуру n В, в положение, при котором n В (напоминаем, что направление нормали n связано с направлением тока правилом правого винта). Площадь, ограниченная контуром, равна S. Найдем работу амперовых сил при указанном перемещении, считая, что ток I поддерживается постоянным.

Согласно (6.40)

A= I [BS – (–BS)] = 2IBS,

Вданном случае работа A > 0, при обратном же повороте A < 0.

Следует отметить, что работа (6.40) совершается не за счет энергии внешнего магнитного поля (оно не меняется), а за счет источника э.д.с., поддерживающего ток в контуре. (Но об этом более подробно будет рассказано в гл. 9.)

Задачи

6.1.Непосредственный расчет индукции В. Ток

I течет по тонкому проводнику, изогнутому, как показано на рис. 6.16. Найти магнитную индукцию В в точке О. Необходимые данные указаны на рисунке.

Решение. Искомая величина В = В– + В , где В– — магнитное поле от прямолинейно-

го участка контура; В> — от его криволи- Рис. 6.16 нейной части. Согласно закону Био—Сава-

ра (см. пример 1 на с. 150)

В результате

B = ( – 0 + tg 0)<0I/2 a.

Полезно убедиться, что при 0 0 мы приходим к известному выражению (6.13).

6.2. Тонкий провод с изоляцией образует плоскую спираль из большого числа N плотно расположенных витков, по которым течет постоянный ток I. Радиусы внутреннего и внешнего витков равны а и b (рис. 6.17). Найти: 1) магнитную индукцию В в центре спирали — точке О; 2) магнитный момент спирали при данном токе.

Решение. 1. Вклад в магнитную индукцию от одного витка радиуса r равен согласно (6.13)

а от всех витков

где dN — число витков в интервале (r, r + dr),

b a

После подстановки (1) и (3) в (2) и последующего интегрирования по r от a до b получим

витков рm рm1dN, где dN определяется формулой (3). Интегрирование дает

6.3.Ток I течет по длинному прямому проводнику, имеющему форму желоба с поперечным сечением в виде тонкого полукольца радиусом R (рис. 6.18). Найти магнитную индукцию В на оси О.

где dI = (I/ )d (см. рис. 6.19). После подстановки (2) в (1) получим

6.4.Теорема о циркуляции В и принцип суперпозиции. Внутри однородного длинного прямого провода круглого сечения имеется круглая цилиндрическая полость, ось которой параллельна оси провода и смещена относительно последней на расстояние l. По проводу течет постоянный ток плотности j. Найти магнитную индукцию В внутри полости.

Решение. Искомую величину можно представить согласно принципу суперпозиции как

где В0 — магнитная индукция в том случае, если бы проводник был сплошным (без полости), а В — магнитная индукция поля в той же точке от тока, текущего по части провода, которую мы удалили, образовав полость круглого сечения.

Таким образом, задача предусматривает прежде всего вычисление магнитной индукции В внутри сплошного провода на расстоянии r от его оси. Воспользовавшись теоремой о циркуляции, запишем 2 rB = <0 r2j, откуда B = <0rj/2. Последнее равенство можно представить с помощью рис. 6.20 в векторной форме:

B = <0[jr]/2.

2. Из того же принципа суперпозиции следует, что нормальная составляющая Вn будет одинакова по площади торца, ибо при образовании составного соленоида Вn + Вn = В0 , где В0 — поле внутри соленоида вдали от его торцов. В центре торца В = Вn, и мы получаем, что В = В0/2.

Решение. Вектор линейной плотности тока i можно представить в виде суммы двух составляющих:

i = i + i−− ,

смысл векторов i и i−− ясен из рис. 6.23, б. В нашем случае модули этих векторов можно найти с помощью рис. 6.23, а по формулам:

i−− = i sin = I/2 a.

Магнитная индукция В внутри соленоида определяется согласно (6.20) величиной i , а вне соленоида — величиной i−−:

Bi <0 i (<0 I / h)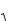1 (h/ 2a)2 (r . a),

Ba = <0i−− a/r = <0I/2 r (r > a),

где при вычислении Ba вне соленоида была использована теорема о циркуляции: 1rВа = <02 ai−−.

Таким образом, представив ток в соленоиде в виде суперпозиции «поперечной» и «продольной» составляющих, мы пришли к выводу, что внутри такого соленоида существует только продольная составляющая поля В, а вне соленоида — только поперечная (как от прямого тока).

Кроме того, если уменьшить ширину ленты, оставляя неизменной плотность тока, то при h 0 сила тока I 0, но I/h = const. В этом случае остается только поле внутри соленоида — соленоид становится «идеальным».

6.7.Взаимодействие параллельных проводников. Два длинных провода с пренебрежимо малым сопротивлением замкнуты с одного конца на сопротивление R, а с другого конца подключены к источнику постоянного напряжения. Радиус сечения каждого провода в , = 20 раз меньше расстояния между осями проводов. При каком значении сопротивления R результирующая сила взаимодействия проводов обратится в нуль?

Решение. На каждом из проводов (протекает по ним ток или нет) имеются избыточные поверхностные заряды (рис. 6.24). Поэтому кроме магнитной силы Fм необходимо учесть и электрическую Fэ . Пусть на единицу длины провода приходится избыточный заряд . Тогда электрическая сила, действующая на единицу длины провода со

стороны другого провода, может быть найдена с помощью теоремы Гаусса:

где l — расстояние между осями проводов. Магнитную же силу, действующую также на единицу длины провода, можно найти с помощью теоремы о циркуляции вектора В:

Fм = (<0/4 )2I2/l,

где I — сила тока в проводе.

Заметим, что обе силы — электрическая и магнитная — направлены в противоположные стороны. Электрическая сила обусловливает притяжение проводов, магнитная — их отталкивание. Найдем отношение этих сил:

Между величинами I и существует определенная связь (см. задачу 2.8):

где U = RI. Поэтому из соотношения (2) следует, что

Зависимость магнитной индукции В от расстояния r до прямого провода находим с помощью теоремы о циркуляции:

Теперь подставим (3) в (2), затем (2) в (1) и, учитывая, что dl = dr и х = r cos , проинтегрируем полученное выражение по r от а до b. В результате найдем

N = (<0/ )II0(b – a) sin ,

причем вектор N направлен влево (см. рис. 6.26).

6.9. Небольшая катушка с током, имеющая магнитный момент рm, находится на оси кругового витка радиусом R, по которому течет ток I. Найти силу F, действующую на катушку, если ее расстояние от центра витка равно l, а вектор рm ориентирован, как показано на рис. 6.27.

где В — магнитная индукция поля, создаваемого витком в месте нахождения катушки. Выберем ось Z в направлении вектора рm, тогда проекция (1) на эту ось будет иметь вид

Fz = pm Bz/ z = pm B/ z,

где учтено, что при заданном направлении тока в витке Вz = В. Магнитная индукция В определяется формулой (6.12), откуда

Вследствие того что дВ/дz < 0, проекция силы Fz < 0, т. е. вектор F направлен в сторону витка с током I. В векторном виде полученный результат можно представить так:

Заметим, что если бы вектор рm (а значит, и ось Z) был направлен в противоположную сторону, то Вz = –В и дВz/дz > 0, а следовательно, Fz > 0 и вектор F был бы направлен вправо, т. е. опять против вектора рm. Таким образом, полученное выражение для F справедливо для обеих ориентаций вектора рm.

6.10.Вдоль длинного тонкостенного круглого цилиндра радиусом R течет ток I. Какое давление испытывают стенки цилиндра? Решение. Рассмотрим поверхностный элемент тока i dS, где i — линейная плотность тока, dS — элемент поверхности. Найдем связь между поверхностным и объемным элементами тока:

j dV = j h · b dl = i dS.

Смысл входящих сюда величин пояснен на рис. 6.28. В векторном виде

где В — магнитная индукция поля в месте нахождения данного элемента тока от всех других элементов тока, исключая данный. Чтобы найти В , поступим аналогично тому, как это было сделано для электри-

ческой силы (§ 2.3). Пусть Вi — магнитная индукция поля, создаваемого самим поверхностным элементом тока в точках, очень близких к его поверхности

(рис. 6.29, где предполагается, что ток течет от нас). Согласно (6.22) Вi = <0i/2.

Далее, воспользовавшись теоремой о циркуляции вектора В и соображениями симметрии, легко установить, что магнитная индукция поля снаружи цилиндра у его поверхности

а внутри цилиндра поле отсутствует.

Последнее означает, что поле В от всех остальных элементов тока в двух очень близких к поверхности цилиндра точках 1 и 2 (см. рис. 6.29) должно быть одинаково и удовлетворять следую-

щим условиям внутри и вне поверхности цилиндра:

B = Bi и B = B + Bi = 2B .

Отсюда следует, что

Подставив этот результат в (2), получим следующее выражение для искомого давления:

Учитывая (3), найдем окончательно p = <0I2/8 2R2.

Из формулы (2) видно, что цилиндр испытывает боковое сжатие.