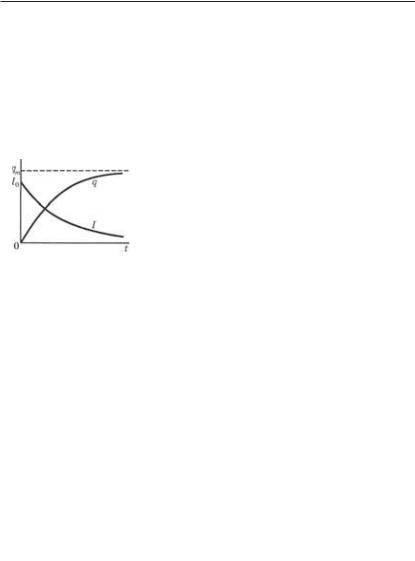
138 Глава 5
откуда |
|
|
q q |
(1 – e–t/0). |
(5.29) |
|
m |
|
Здесь qm С — предельное значение заряда на конденсаторе (при t %), RC. Закон изменения тока со временем
I |
dq |
I |
0e t /0 , |
|
|
(5.30) |
|||
|
dt |
|
|
|
где I0 /R.
Графики зависимостей q(t) и I(t) показаны на рис. 5.13.
Рис. 5.13
Задачи
5.1.Сопротивление проводящей среды. Металлический шар радиусом
а окружен концентрической тонкой металлической оболочкой радиусом b. Пространство между этими электродами заполнено од-
нородной слабо проводящей средой с удельным сопротивлением . Найти сопротивление межэлектродного промежутка.
Решение. Выделим мысленно тонкий сферический слой между радиусами r и r + dr. Линии тока во всех точках этого слоя идут перпендикулярно ему, поэтому такой слой можно рассматривать как цилиндрический проводник длиной dr с площадью поперечного сечения 4 r2. Воспользовавшись формулой (5.9), запишем
dr dR 
.
4 r2
Проинтегрировав это выражение по r от а до b, получим
|
|
|
1 |
1 |
|
|
R |
|
! |
|
|
|
. |
|
|
|
||||
|
4 |
! a |
b |
|
||
|
|
|
|
|
|
# |
5.2.Два металлических шарика одинакового радиуса а находятся в однородной слабо проводящей среде с удельным сопротивлением. Найти сопротивление среды между шариками при условии, что расстояние между шариками значительно больше их размеров.
Постоянный электрический ток |
139 |
|
|
Решение. Мысленно зарядим шарики +q и –q. Поскольку шарики находятся далеко друг от друга, электрическое поле вблизи поверхности каждого из них определяется практически только зарядом самого шарика, причем его заряд можно считать распределенным равномерно по поверхности. Окружив шарик с положительным зарядом концентрической сферой, непосредственно прилегающей к его поверхности, запишем выражение для тока, протекающего через эту сферу:
I 4 a2j,
где j — плотность тока. Воспользовавшись законом Ома (j Е/ ) и формулой Е q/4 0a2, получим
I q/ 0 .
Теперь найдем разность потенциалов между шариками:
U + – – 2q/4 0a.
Искомое сопротивление
R U/I /2 a.
Этот результат справедлив независимо от значения диэлектрической проницаемости среды.
5.3.Два проводника произвольной формы находятся в безграничной однородной слабо проводящей среде с удельным сопротивлением и диэлектрической проницаемостью . Найти значение произведения RC для данной системы, где R — сопротивление среды между проводниками, С — взаимная емкость проводников при наличии среды.
Решение. Зарядим мысленно проводники зарядами +q и –q. Так как среда между ними слабо проводящая, то поверхности проводников являются эквипотенциальными и конфигурация поля такова же, как и при отсутствии среды.
Окружим, например, положительно заряженный проводник замкнутой поверхностью S, непосредственно прилегающей к поверхности проводника, и вычислим отдельно R и С:
R U U U ,
I KjndS KEndS
C q KDndS 0KEndS ,
U U U
140 |
Глава 5 |
|
|
где интегралы взяты по данной поверхности S. При вычислении R был использован закон Ома j Е, а при вычислении С — теорема Гаусса.
Произведение полученных выражений
RC 0 / 0 .
5.4.Условия на границе проводника. Проводник с удельным сопротивлением граничит с диэлектриком, проницаемость которого . В некоторой точке А у поверхности проводника электрическая индукция равна D, причем вектор D направлен от проводника и со-
ставляет угол с нормалью к поверхности. Найти поверхностную плотность зарядов на проводнике и плотность тока вблизи точки А.
Решение. Поверхностная плотность зарядов на проводнике
Dn D cos .
Плотность тока найдем по закону Ома: j = Е/ . Из уравнения непрерывности (5.5) следует, что нормальные составляющие вектора j равны, а так как в диэлектрике jn = 0 (тока нет), то и в проводнике jn = 0. Стало быть, вектор j в проводнике касателен его поверхности. Это же относится и к вектору Е внутри проводника.
С другой стороны, из теоремы о циркуляции вектора Е следует, что тангенциальные составляющие его по разные стороны границы раздела одинаковы, а значит, Е Е0 = (D/ 0) sin , где E0 — тангенциальная составляющая поля Е в диэлектрике.
Учитывая все это, получим
j E D sin .
0
5.5.Зазор между обкладками плоского конденсатора заполнен последовательно двумя диэлектрическими слоями 1 и 2 толщиной l1 и l2 с проницаемостями 1 и 2 и удельными сопротивлениями 1 и2. Конденсатор находится под постоянным напряжением U, причем электрическое поле направлено от слоя 1 к слою 2. Найти поверхностную плотность сторонних зарядов на границе раздела диэлектрических слоев.
Решение. Искомая поверхностная плотность зарядов
D2n – D1n 0 2E2 – 0 1E1. |
(1) |
Постоянный электрический ток |
141 |
|
|
Для определения E1 и E2 воспользуемся двумя условиями: из того
факта, что j1 = j2, следует Е1/ 1 = Е2/ 2 и, кроме того, Е1l1 + Е2l2 = U. Решив два последних уравнения, найдем E1 и E2. Их подстановка в
(1)приводит к следующему результату:
2 2 1 1 0U .
1 l1 2 l2
Отсюда видно, что 0 при 1 1 = 2 2.
5.6.Неоднородный проводник. Длинный проводник круглого сечения площадью S сделан из материала, удельное сопротивление которого зависит только от расстояния r до оси проводника как
/r2, где — постоянная. По проводнику течет ток I. Найти: 1) напряженность Е поля в проводнике; 2) сопротивление единицы длины проводника.
Решение. 1. Напряженность Е поля по закону Ома связана с плотностью тока j, а j — с током I, поэтому можно записать
I j 2 r dr (E / )2 r dr.
Напряженность Е одинакова во всех точках сечения данного проводника, т. е. не зависит от r. В этом легко убедиться, взяв прямоугольный контур внутри проводника так, чтобы одна сторона контура совпадала, например, с осью проводника, и затем применив к этому контуру теорему о циркуляции вектора Е.
Таким образом, Е можно вынести из-под интеграла и мы получим в результате интегрирования
E= 2 I/S2.
2.Сопротивление единицы длины проводника можно определить с помощью формулы R = U/I. Поделив обе части этого равенства на длину l участка проводника, к которому относятся R и U, найдем
Rед = E/I = 2 /S2.
5.7.Закон Ома для неоднородного участка цепи. В схеме (рис. 5.14) изве-
стны э.д.с. и 0 источников, сопротивления R и R0, а также емкость С конденсатора. Внутренние сопротив-
ления источников пренебрежимо малы. Найти заряд на обкладке 1
конденсатора. |
Рис. 5.14 |
|
142 |
Глава 5 |
|
|
Решение. В соответствии с законом Ома для замкнутой цепи, содержащей сопротивления R и R0, запишем
(R + R0)I = – 0,
где положительное направление выбрано по часовой стрелке. С другой стороны, для неоднородного участка aRb цепи
RI = a – b + ,
а для участка aCb
+ 2 – 1 = b – a.
Решив совместно эти три уравнения, получим
|
R |
|
1 2 |
|
( 0 ). |
|
||
|
R R0 |
|
Заряд на обкладке 1 определяется формулой q1 = С( 1 – 2). Поэтому окончательный результат
|
RC |
|
q1 |
|
( 0) . |
|
||
|
R R0 |
|
Видно, что при > 0 заряд q1 > 0, и наоборот.
5.8.Работа источника э.д.с. Стеклянная пластина целиком заполняет зазор между обкладками плоского конденсатора, емкость которо-
го при отсутствии пластины равна С0. Конденсатор подключен к источнику постоянного напряжения U. Найти механическую ра-
боту, которую необходимо совершить против электрических сил, чтобы извлечь пластину из конденсатора.
Решение. Согласно закону сохранения энергии
Aмех + Aист W, |
(1) |
где Амех — совершенная внешними силами механическая работа против электрических сил; Aист — работа источника в этом процессе; W — соответствующее приращение энергии конденсатора (мы считаем, что участие других видов энергии в изменении энергии системы пренебрежимо мало).
Найдем W и Aист. Из формулы для энергии конденсатора (W = = CU2/2 = qU/2) следует, что при U = const
W = C U2/2 = q U/2. |
(2) |
Постоянный электрический ток |
143 |
|
|
Так как емкость конденсатора при извлечении пластины уменьшается ( С < 0), то уменьшается и заряд конденсатора ( q < 0). Последнее означает, что заряд прошел через источник против направления действия сторонних сил и источник совершил отрицательную работу:
Aист = q U. |
(3) |
Из сравнения формул (3) и (2) следует
Aист = 2 W.
После подстановки последнего выражения в (1) получим
Aмех = – W, или Aмех = ( – 1)C0U2/2.
Таким образом, извлекая пластину из конденсатора, мы (внешние силы) совершаем положительную работу (против электрических сил), при этом источник э.д.с. совершает отрицательную работу и энергия конденсатора уменьшается:
Aмех > 0, Aист < 0, W < 0.
5.9.Переходные процессы. Цепь состоит из источника постоянной э.д.с. E и последовательно подключенных к нему сопротивления R и конденсатора С. Внутреннее сопро-
тивление источника пренебрежимо мало. В момент t = 0 емкость конденсатора бы-
стро (скачком) уменьшили в , раз. Най- |
|
ти ток в цепи как функцию времени. |
|
Решение. Запишем закон Ома для неод- |
|
нородного участка цепи 1 R2 (рис. 5.15): |
Рис. 5.15 |
RI = 1 – 2 – = U – . |
|
Учтем, что U = q/C , где С = С/,, тогда |
|
RI = q/C – . |
(1) |
Продифференцируем это равенство по времени, принимая во внимание, что в нашем случае (q уменьшается) dq/dt = –I:
R |
dI |
|
, |
I , |
dI |
|
, |
dt. |
dt |
|
|
|
|||||
|
C |
I |
|
RC |
||||
Интегрирование последнего уравнения дает
ln |
I |
|
,t |
, I I |
0e,t / RC, |
|
|
||||
|
I 0 |
|
RC |
|
|
144 |
Глава 5 |
|
|
где I0 определяется условием (1). Действительно,
RI0 = ,q0/C – ,
причем q0 = C — заряд конденсатора до изменения его емкости. Поэтому
I0 = (, – 1) /R.
5.10.Конденсатору емкостью С сообщили заряд q0 и затем в момент t = 0 его замкнули на сопротивление R. Найти зависимость от
времени t количества теплоты, выделившегося на сопротивлении.
Решение. Искомое количество теплоты
t |
|
Q RI 2 dt, |
(1) |
0 |
|
откуда видно, что прежде всего надо найти зависимость I(t). Воспользуемся с этой целью законом Ома для участка цепи 1R2 (рис. 5.16):
|
|
|
|
|
|
|
|
|
|
|
|
RI = 1 – 2 = U, |
|
|
Рис. 5.16 |
или |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
RI = q/C. |
(2) |
|
Продифференцируем (2) по времени: |
|
|||||||||||||
R |
dI |
|
1 |
I , |
|
dI |
|
dt |
. |
|
||||
|
dt |
|
|
|
|
|||||||||
|
|
|
C |
|
I RC |
|
||||||||
Проинтегрировав последнее уравнение, получим |
|
|||||||||||||
ln |
I |
|
|
t |
, |
I I 0e t / RC, |
|
|||||||
|
|
(3) |
||||||||||||
|
|
I 0 |
|
|
RC |
|
|
|
|
|
|
|||
где I0 определяется условием (2) при q = q0, т. е. I0 = q0/RC.
После подстановки (3) в (1) и соответствующего интегрирования получим
2
Q q0 (1 e 2t / RC ).
2C