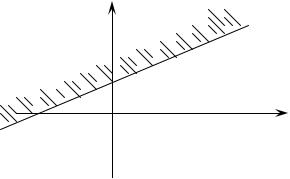
x2

a1x1+ a2x2 ≤ λ

Рис.3. Замкнутое пространство на плоскости

Пусть х' и х'' – две произвольные точки этого множества. Для них по условию выполнены неравенства

(а,х') ≥ λ, (а,х'') ≥ λ.

Тогда для любого t [0,1] будем иметь:

t(a,x') ≥ tλ; (1–t)(a,x'') ≥ (1–t)λ;

t(a,x')+(1–t)(a,x'') ≥ tλ + (1–t)λ; (a,tx' + (1–t)x'') ≥ λ.

Таким образом, отрезок, соединяющий точки х' и х'' принадлежит рассматриваемому множеству в силу произвольности t [0,1].

Пересечение выпуклых множеств представляет собой выпуклое множество.

3.3. Функция нескольких переменных и ее свойства

Функция f (x1, x2, …, xn), область определения которой представляет собой множество точек x пространства Rn

G= {(x1, x2 ,..., xn )} Rn ,

азначения являются действительными числами (U = {u} R) называется

25

функцией n переменных и обозначается

u = f (x), x G ,

или

u = f (x1,x2,…,xn ), где (x1,x2,…,xn) G

Функция f называется непрерывной в точке х0, если для любого ε > 0 существует δε > 0, что для любого x U(x0,δε) выполняется условие

|f (x) – f (x0)| < ε

и называется непрерывной на множестве G, если она непрерывна в каждой точке G .

Например, линейная функция

непрерывны на Rn.

Пусть х0 = (x10,x20,…,xn0) – фиксированная внутренняя точка множества G.

Функция f называется дифференцируемой в точке х0, если существует ее производная

Функция, дифференцируемая в каждой точке открытого множества G, называется дифференцируемой на множестве G (или просто дифференцируемой, если G=Rn).

Функция многих переменных f, имеющая в точке х0 (на множестве G) непрерывные частные производные первого порядка, называется непрерывно дифференцируемой в этой точке (на множестве G).

Функция f (x1, x2, …, xn) называется сепарабельной, если ее можно записать в виде суммы функций одной переменной f1(x1), f2(x2), …, fn(xn),

26

т.е.

f (x1, x2, …, xn) = f1(x1) + f2(x2) + … + fn(xn).

Например, линейная функция

h(x1, x2, …, xn) = a1x1 + a2x2 + … + anxn

(где все аi, i= 1,n – постоянные числа) является сепарабельной, а функция

h(x1, x2, x3) = x1 +sin(x2 + x3) + x2

сепарабельной не является. Вектор

называется градиентом функции f в точке х0, обозначается символом f (x0) (читается: "набла эф от х0''), где

= ∂∂x1 , ∂∂x2 ,..., ∂∂xn

−символический оператор Гамильтона, и пишут

Вектор −f (x0) называется антиградиентом функции f в точке x0. Градиент функции f указывает направление наискорейшего возрастания, а антиградиент – направление наискорейшего убывания ее

значений в точке х0.

Функция f, заданная на выпуклом множестве G Rn, называется выпуклой, если x1x2 G и t [0,1] выполняется неравенство

и называется вогнутой, если функция −f (противоположная функция) выпукла на множестве G.

27

Выпуклые функции определяются только на выпуклых множест-

вах.

В случае действительного аргумента x R функция f (x) называется выпуклой, если для любых х1 и х2 из интервала допустимых значений выполняется условие:

Геометрически условие (3.15) означает, что середина любой хорды графика функции f лежит либо над графиком, либо на нем.

Если неравенства (3.14), (3.15) выполняются, как строгие, то f – строго выпуклая функция.

Справедливы следующие утверждения.

1) Если функции f1,f2,…, fm выпуклы на выпуклом множестве G, то функция

m

f (x) = ∑ck fk (x),

k =1

где сk ≥ 0, k = 1,2, ...,m, выпукла на G.

2) Если функция выпукла на выпуклом множестве G, то α R множество

{ x G f (x) ≤α }

является выпуклым.

3) Пусть функция f непрерывно дифференцируема на выпуклом множестве G. Тогда f выпукла на G, следовательно

Необходимое и достаточное условие выпуклости функции:

Если функция f дифференцируема на интервале, то для того, чтобы она была (строго) выпуклой на нем, необходимо и достаточно, чтобы ее производная возрастала (не убывала).

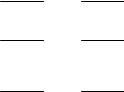
Таким образом, для выпуклости непрерывно дифференцируемой функции на некотором множестве G достаточно неотрицательной определенности ее матрицы вторых частных производных Гессе:

28