Алгоритм поиска методом Ньютона:

1.Ввод интервала [a,b], eps.

2.Выбор начального приближения:

Проверяем условие (7.22) для точки a. Если оно выполняется, полагаем х=а и переходим на п.3. Иначе проверяем условие (7.22) для точки b, если оно выполняется, то полагаем х=b и переходим на п.3, иначе на п.1.

3.Вычисляем вспомогательный параметр

T= f0 '(x) f0"(x)

иследующее приближение к точке минимума х = х – Т.

4.Проверка условия (7.21) окончания процесса итераций:

T ≤ eps ?

Нет – переход на п. 3; иначе на п. 5.

5.Печать "х*= ", х, оптимального значения критерия f0(x), для контроля правильности полученных данных – f0'(х).

7.14.Методы поиска безусловного экстремума невыпуклых функций

Во многих оптимизационных задачах используют целевые функции f0(x) (где х принадлежит области допустимых значений D) степень выпуклости которых заранее неизвестна. Такие функции могут иметь произвольное число точек минимума, либо быть невыпуклыми и обладать произвольным числом стационарных точек, среди них есть и точки минимума, максимума, перегиба.

Поиск безусловного минимума невыпуклой функции имеет ряд особенностей, так как для такой функции уравнение f0'(х) всегда имеет несколько, в том числе и. бесконечно много решений хс, что затрудняет выбор из них точек минимума.

Наличие нескольких локальных минимумов делает фактически невозможным применение ряда итерационных методов поиска экстремумов, так как при этом возникает проблема подбора "хороших" началь86

ных приближений х0, расположенных близко к каждой μ-й точке мини-

мума xμ* , μ=1,2,... .

Стратегия поиска локального и глобального минимумов невыпуклой функции f0(x):

1.Методом сканирования осуществляется грубый анализ тополо-

гии функции f0(x); по ординатам f0(xk) выявляются локальные максимумы f0+(xj), j = 1,2,… и минимумы f0−(xμ), μ = 1,2,… .

Множество D разбивается на ряд соприкасающихся подмножеств Dj, j = 1,2,… граничными (разделяющими) точками которых служат xj, j = 1,2,… .

2.Для каждого подмножества Dj задается два начальных прибли-

жения 1 x0j и 2 x0j , j =1,2,... .

3.Для каждого начального приближения 1 x0j и 2 x0j методом одномерного градиента находятся точки локального минимумов

начальных приближений 3 x0j , 4 x0j и более детально исследовать методом одномерного градиента расположение локального минимума

4. Непосредственным сравнением ординат f0 (k x*j ), k =1,2,3,4,..., j =1,2,3,... находится глобальный минимум

f0 (x*) = min f0 (k x*j )

k

и соответствующая ему точка x*, принадлежащая множеству D.

87

7.15. Метод тяжелого шарика

Для поиска глобального минимума невыпуклой функции, которая имеет "неглубокие" локальные минимумы, находят применение многошаговые методы, использующие на k-й итерации значения f0(x).

Идея использования метода "тяжелого шарика" и его названия основаны на физической интерпретации процесса качения шарика по наклонной поверхности. Если шарик тяжелый, то он будет проскакивать мелкие впадины по инерции. Чем больше масса шарика, тем глубже будет впадина, в которой он остановится.

Двухшаговая итерационная процедура поиска глобального минимума f0(x) методом "тяжелого шарика" имеет следующий вид

где k – номер итерации (k=1,2,...,). h, β параметры, которые подбираются в процессе решения задачи.

Скорость приближения {xk} к х* зависит не только от "крутизны" функции в точке xk, характеризуемой величиной f0'(xk) , но и от "инерции" последовательности {xk}, которая пропорциональна слагаемому

β (xk − xk −1) . При попадании точки xk в локальный минимум x€ произ-

должна отличатся от нуля, поэтому

xk +1 = xk + β (xk − xk −1)

и последовательность {xk} продолжит движение к х*. Подобная особенность итерационного метода "тяжелого шарика" позволяет "проскакивать" по инерции мелкие, неглубокие локальные минимумы и останавливаться в точках глобального экстремума. Окончание процесса итерации

xk +1 − xk ≤ ε. .

88

Алгоритм поиска минимума методом тяжелого шарика:

1.Вводим два приближения х0 и х1, вычисляем значения критерия f0 = f (х0) и f1 = f (x1).

2.Вычисляем значение производной R = f '(x1).

3.Вычисляем предполагаемую точку минимума х по формуле

x= x1 − h R + β (x1 − x0 ) .

4.Вычисляем f = f (x). Проверяем условие улучшаемости f < f1?

"Да" – проверяем условие x − x1 ≤ ε, , если выполняется, то пе-

реходим на п.6, иначе − на п.5; нет – за точку минимума принимаем точку х1, то есть х = х1 и переходим на п.6, либо можно изменить параметры h или β и продолжить поиск минимума в окрестности точки х1.

5.Переопределяем точки х0 = х1; х1 = х и переходим на п.2.

6.Печать "х*= ", х, оптимального значения критерия f0(x), для кон-

троля правильности полученных данных – f0'(x).

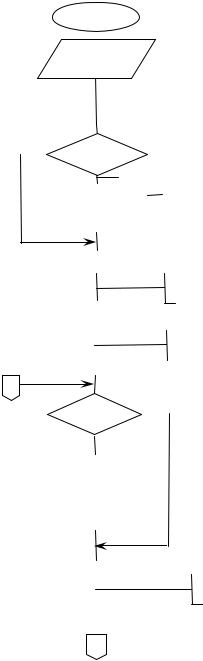
Блок-схема рассмотренного метода приведена на рисунке 14(а,б). В алгоритме предусмотрен выбор параметров в процессе решения задачи на ЭВМ. При величине шага меньшей заданной точности выполняется переход на п.6. Критерий цели и f '(x) заданы функциями пользователя f и pr соответственно.

Текст программы на языке Турбо-Паскаль:

program tiag_shar;

Var x0,x1,h,b,f0,f1,ff,c,x:real; k,p,n,i:byte; const eps=1e–7;

function f(x:real):real; begin f:=x*sqr(x)+2*sqr(x)–x+3 end;

function pr(x:real):real; begin pr:=3*sqr(x)+4*x–1 end;

89

begin x:= –5;

for i:=1 to 20 Do begin

Writeln(' x= ',x,' pr= ',pr(x)); x:=x+0.5;

end; readln;

Write('x0,x1?'); readln(x0,x1); f0:=f(x0); f1:=f(x1);

if f1>f0 then begin

c:=x1; x1:=x0; x0:=c {переобозначаем точки} end;

p:=0; { p=0 – меняем b, p=1 – меняем h} {b:=0.4;} b:=0.3; h:=0.2; n:=0;

k:=0; {k=1 переопределяем точки x0,x1 } repeat

if k=1 then begin

x0:=x1; x1:=x; {переопределяем точки} end;

k:=0;

n:=n+1; {увеличиваем число итераций} {находим следующее приближение}

x:=x1–h*pr(x1)+b*(x1–x0); {вычисляем целевую функцию}

{для следующего приближения} ff:=f (x);

{проскочили минимум?}

if (ff>f1) and (p=0) and (b–0.1>0) then b:=b–0.1 else

if (b–0.1)<=0 then p:=1;

if (ff>f1) and (p=1) and (h>=eps) then h:=h/2; if ff<f1 then k:=1;

untiL (abs(x1–x)<eps) or (h<eps); Writeln(' x*= ',x,' min f= ',f (x),

' Df/Dx= ',pr(x),' b= ',b,' h= ',h,' n= ',n);

end.

90

2

Рис.14а. Блок-схема поиска минимума методом тяжелого шарика

91

Ошибка!

Да Печать

'x*= ',x,' min f= ',f (x),

'df/dx= ',pr(x),' b= ',b,

'h= ',h,' n= ',n.

Конец

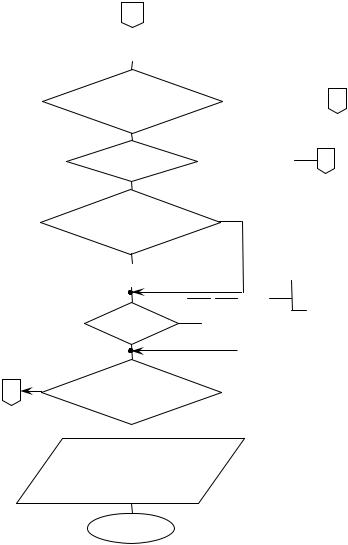
Рис.14б. Продолжение блок-схемы поиска минимума методом тяжелого шарика

92