и достаточные условия).

Условия, при выполнении которых хотя бы одна седловая точка функции Лагранжа всегда существует, сформулированы в следующем утверждении.

Теорема 5.4:

Пусть функции f, gi , i=1,2,...,m, выпуклы на выпуклом множестве G Rn , имеет место условие (условие Слейтера):

и х* – точка глобального минимума в задаче (5.1). Тогда найдется такой вектор λ* R+m , что пара (x*,λ*) – седловая точка функции Лагранжа

(5.2).

Эта теорема представляет собой необходимое условие оптимальности: для того чтобы х* была точкой глобального минимума в выпуклой задаче оптимизации (5.1), необходимо, чтобы нашелся такой вектор λ*, что пара (х*,λ*) образует седловую точку функции Лагранжа.

Таким образом, с помощью теорем 5.2 и 5.4 исходную задачу (5.1) можно заменить задачей отыскания седловой точки функции Лагранжа.

6. МЕТОДЫ РЕШЕНИЯ ОПТИМАЛЬНОЙ ЗАДАЧИ ДЛЯ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ

Среди многочисленных оптимизационных задач особое место занимает задача на безусловный минимум функции f0(x) одной переменной. Это объясняется простотой и наглядностью методов ее решения. Кроме того, эти методы находят широкое применение при поиске экстремума функции многих переменных.

Для решения задач минимизации функции f0(x) одной переменной разработало большое число разнообразных методов, которые базируются в основном на необходимых и, реже на достаточных условиях экстре-

55

мума функции.

Многообразие методов поиска экстремума f0(x) обусловлено тем, что каждый из них использует различную информацию о способах описания функции и ее математических свойствах, как-то дифференцируемость, выпуклость, число экстремумов и т.д.

6.1. Необходимые и достаточные условия экстремума функции одной переменной

Необходимое условие:

Пусть функция f (x) непрерывна и определена на открытом множе-

стве D = {x | x− < x < x+}.

Найти управление x*, принадлежащее множеству D, такое, что

Уравнение (6.2) – это необходимое условие экстремума функции одной переменной. Оно выделяет только стационарные точки xc, в которых функция не возрастает и не убывает. В число стационарных точек xc входят точки min, max, перегиба функции. В точках перегиба слева от x* функция возрастает (убывает), а справа – убывает (возрастает).

Достаточное условие

Пусть f0(x) дважды дифференцируема по х, принадлежащему множеству D. Если в точке x* выполняется условие

то точка x* является точкой локального (глобального) минимума функции.

56

Если выполняется условие

то точка x* – локальный (глобальный) максимум.

В точке перегиба xc функции f0(x) ее первая и вторая производные равны нулю, а слева и справа от xc производная имеет разные знаки:

Существуют два подхода для решения задачи (6.1):

1)аналитический метод, использующий необходимое условие экстремума;

2)итерационный метод.

6.2.Алгоритм аналитического метода

1.Получение математического выражения для первой производ-

ной f0 '(x*) = 0 .

2.Анализ уравнения (6.2) с целью выбора метода ее решения: аналитического или численного.

3.Нахождение аналитического (формульного) решения xc или корней (нулей) уравнения (6.2).

4.Анализ полученных стационарных точек с целью выделения из них точек минимума, максимума, перегиба.

5.Вычисление значения критерия в точках локального минимума, максимума и в граничных точках (если множество D закрытое). Сравнение значений критерия и выбор наибольшего и наименьшего значений.

Аналитическое решение уравнения (6.2) удается найти в сравнительно редких случаях:

1)Когда в функцию f0(x) входят экспонента, тригонометрические функции sin(х), cos(х).

57

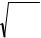
2)Когда f0(x) представляет собой степенной многочлен, не выше пятого порядка.

Пример 7:

Функция f0(x) =3x4 −4x3 −12x2 +2 определена на отрезке [-2,3].

Вычисляем f0'(x) =12x3 −12x2 −24x . Из условия (6.2) находим стационарные точки: 12x(x2 – x – 2) = 0. По теореме Виетта находим:

Вычисляем вторые производные в стационарных точках:

f0"(x) = 36x2 − 24x − 24 f0"(0) = −24 < 0 – локальный максимум f0"(−1) = 36 > 0 – локальный минимум f0"(2) = 72 > 0 – локальный минимум

Вычисляем значения функции f0(x) на границе f0 (−2) = 48 + 32 − 48 + 2 = 34

f0 (−1) = 3 + 4 −12 + 2 = −3 f0 (0) = 2

f0 (1) =11 f0 (2) = −30 f0 (3) = 29

Находим глобальные min f0 = f0 (2) = −30 и max f0 = f0 (−2) = 34 .

58