7. ИТЕРАЦИОННЫЕ МЕТОДЫ ОПТИМИЗАЦИИ

Для большинства оптимизационных задач нахождения аналитического решения уравнения (6.2) вызывает существенные, а часто и непреодолимые трудности. Тогда используют итерационные (приближенные) методы поиска решения x* оптимизационной задачи на открытом мно-

жестве D = {x | x− < x < x+}.

Итерация – многократное выполнение одного и того же действия. Итерационные методы решения оптимизационной задачи заключаются в многократном применении одной и той же математической операции к xk и получения последовательности точек x1, x2,…, xk (где k – номер итерации k = 0,1,2,….), сходящейся к точному решению x*, т.е.:

7.1.Алгоритм итерационного метода

1.Выбирается начальное приближенное x0, (желательно x0 выбирать в окрестности точки x*).

2.Через известное k-ое приближение xk (где k – номер итерации k=0,1,2,...) из множества D и значения f0(xk), f0'(xk), f0"(xk) вычисляется новое k+1 приближение по формуле:

3.На каждом шаге итерации проверяется условие улучшаемости решения задачи минимизации

4.Если условие (7.3) выполняется, то xk = xk+1, f k = f k+1, k = k+1 и переходим на п.2, если нет, то переходим к п.5.

59

5.При нарушении условия (7.3) осуществляется либо уменьшение шага x и вычисление нового приближения, либо остановка итерационной процедуры (если | x| ≤ eps, где eps – погрешность) и точка xk объявляется приближенным решением x* экстремальной задачи.

В зависимости от структуры зависимости x итерационные методы делятся на три группы:

1)нулевого порядка ( x зависит от f0(xk) или от шага h);

2)первого порядка ( x определяется через f0(xk) и f0'(xk)) (методы одномерного градиента, тяжелого шарика);

3)второго порядка ( x зависит от f0(xk), f0'(xk), f0"(xk)) (метод

Ньютона).

К числу методов нулевого порядка относятся методы сканирования, дихотомии, "золотого" сечения, чисел Фибоначчи и квадратичной интерполяции.

Порядок итерационной процедуры существенно влияет на скорость приближения xk к x*.

Использование в x информации о скорости изменения f0'(xk), в точке xk, и тем более об ускорении f0"(xk) позволяет увеличивать на каждой итерации шаг x, и расстояние (xk − x*) будет убывать тем быстрее, чем выше порядок итерационной процедуры. Грубо говоря, число итераций уменьшается приблизительно в 10 раз при увеличении порядка метода на 1.

Применение итерационных методов высокого порядка для поиска экстремума f0(x) хотя и приводит к уменьшению числа итераций k, но не всегда позволяет сократить при этом объем необходимых вычислений на ЭВМ, так как для плохо дифференцируемых f0(x) вычисление производных более трудоемко, чем вычисление самих функций. Поэтому чаще всего используются итерационные методы нулевого и первого порядка.

60

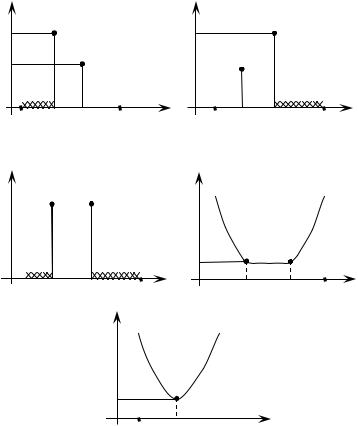
7.3. Определение унимодальной функции

Функция f0(x) является унимодальной на отрезке a ≤ x ≤ b, если она непрерывна на [a,b], и существуют числа α, β, a ≤ α ≤ β ≤ b, такие что

1)f0(x) строго монотонно убывает при a ≤ x ≤ α (если a < α);

2)f0(x) строго монотонно возрастает при β ≤ x ≤ b (если β < b);

f0*

Рис.9. Определение интервала, содержащего точку х*, для унимодальной функции цели

62