-y

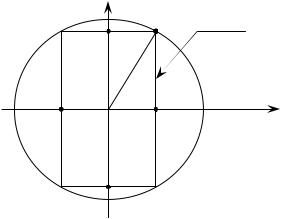
Рис.1. Прямоугольник, вписанный в круг на координатной плоскости

Любая формализованная оптимизационная задача, в основном, устроена аналогично. Она включает в себя некоторую функцию

f : Ω → R

(Ω – область определения функции f), называемую целевой функцией или критерием оптимальности, и подмножество G Ω, называемое множеством возможных решений, на котором требуется определить наименьшее или наибольшее значение функции f.

Методы решения оптимизационных задач зависят как от вида целевой функции f, так и от структуры множества возможных решений G.

2.2. Аппроксимация экспериментальных данных

При экспериментальном исследовании статических характеристик некоторого линейного технологического объекта управления (ТОУ) получено n значений входной и выходной координат. Требуется найти аналитическую зависимость, наилучшим образом описывающую экспериментальные данные.

Для формализации задачи введем обозначения: zi, yi – входная и выходная координаты ТОУ в i-м опыте, i=1,2,…,n;

9

Аналитическая статическая характеристика линейного ТОУ имеет

вид

yр = x·z,

где x – неизвестный коэффициент, подлежащий определению по данным

zi, yi, i =1, ni (x – свободная переменная или управление для рассматриваемой задачи).

Цель задачи – наилучшая аппроксимация данных zi, yi – может количественно характеризоваться несколькими целевыми функциями, в частности:

f1 = max yi − x zi ,

Критерий f1 характеризует наибольшее отклонение прямой y=x·z от какой-либо "худшей" опытной точки {zi,yi}. Использование такого "точечного" критерия опасно, когда опытные данные содержат грубые ошибки. Функция f1 имеет разрывы первого рода по x, что существенно затрудняет ее применение для оценки качества аппроксимации опытных данных.

Критерий f2 представляет усредненную меру удаления прямой y=x·z от всех опытных данных, причем весомость больших и малых отклонений или "невязок" |yi – x zi| здесь одинакова. Критерий имеет отчетливую физическую трактовку, однако его математическое свойство – недифференцируемость в точке минимума – затрудняет применение f2 для аппроксимации опытных данных.

Третий критерий – средний квадрат отклонения прямой от данных {zi,yi} учитывает существенность больших отклонений |yi – x zi| и незначимость малых. Критерий f3 дифференцируется всюду, и его целесообразно использовать для оценки качества аппроксимации.

Выбранный критерий оптимальности f3 зависит от одной перемен10

ной x, которая по условиям задачи может принимать любые значения на числовой оси (–∞, +∞), т.е. на "свободную" переменную не накладывается каких-либо условий или ограничений.

Оптимизационная задача формализуется в следующем виде: найти переменную x, обеспечивающую минимум критерия

Таким образом, задача наилучшей аппроксимации опытных данных сформулирована в виде задачи на безусловный минимум функции одной переменной.

2.3. Выбор места расположения управляющей вычислительной машины на производстве

Для технологического процесса, автоматизируемого с помощью УВМ, известны места установки датчиков и исполнительных механизмов (ИМ). Требуется выбрать наилучшее место расположения УВМ с тем, чтобы сократить расходы на линии связи.

Вданной производственной задаче целью является экономия денежных средств на кабельную продукцию. За целевую функцию можно выбрать суммарную стоимость линии связи от УВМ к датчикам и ИМ. При линейной зависимости стоимости от длины эта функция может трансформироваться в сумму длин кабелей от УВМ до датчиков и ИМ.

Вкачестве "свободных" переменных (управлений) в задаче выступают координаты места расположения УВМ на плоскости, которые можно обозначить как x и у. Тогда координаты известных точек уста-

новки датчиков и ИМ обозначаются как {xi , yi }, i =1, n , где n – суммарное число датчиков и ИМ.

Критерий оптимальности – сумма отрезков от неизвестной точки {xi,yi} до n известных точек {xi , yi }, i =1, n обозначается через f0 и выражается через переменные x, y:

11

n

f0 (x, y) = ∑ (x − xi )2 + ( y − yi )2

i =1

По условию задачи переменные x, y могут изменяться на интервале (–∞, +∞), т.е. множество допустимых решений задачи есть вся числовая плоскость с бесконечным числом элементов.

Непосредственная постановка оптимизационной задачи: найти такие переменные x, y, при которых принятый критерий оптимальности достигнет наименьшего значения.

Математическая модель:

Таким образом, сформулирована задача на минимум функции двух переменных x, y без каких-либо дополнительных условий на множество допустимых решений (задача на безусловный минимум функции многих переменных).

2.4. Выбор места расположения УВМ в производственном здании

Словесное описание данной задачи совпадает с описанием предыдущей задачи за исключением условия на место расположения УВМ: ее можно устанавливать в здании с известными координатами x−, x+; y−, y+.

Тогда управляемые переменные задачи могут изменяться в определенном диапазоне, задаваемом размерами здания:

x− ≤ x ≤ x+, y− ≤ y ≤ y+.

Такого рода ограничения называются автономными.

Эти два неравенства определяют множество допустимых решений задачи, обозначаемое через D.

D = {x, y | x− ≤ x ≤ x+, y− ≤ y ≤ y+} ,

где символ "|" имеет смысл "таких, что".

12