
- •1. ОСНОВНЫЕ ПОНЯТИЯ
- •2.1. Формализация геометрической задачи
- •2.2. Аппроксимация экспериментальных данных
- •2.3. Выбор места расположения управляющей вычислительной машины на производстве
- •2.4. Выбор места расположения УВМ в производственном здании
- •2.5. Определение оптимальных настроек АСР
- •2.6. Распределение нагрузки между параллельными агрегатами
- •2.7. Оптимизация температурного режима реактора периодического действия
- •3. ОСНОВНЫЕ ПОНЯТИЯ АЛГЕБРЫ И АНАЛИЗА
- •3.1. Общие сведения о множествах
- •Рис.2. Графическое представление операций над множествами
- •3.2. Евклидово пространство
- •3.3. Функция нескольких переменных и ее свойства
- •4. ПОСТАНОВКА ЗАДАЧИ ОПТИМИЗАЦИИ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ. УСЛОВИЯ ОПТИМАЛЬНОСТИ
- •4.1. Целевая функция. Локальный и глобальный оптимумы
- •4.2. Разрешимость задачи оптимизации
- •4.3. Задачи оптимизации без ограничений
- •4.4. Задачи оптимизации с ограничениями типа равенств. Метод неопределенных множителей Лагранжа
- •4.5. Задачи с ограничениями типа неравенств
- •5. ВЫПУКЛЫЕ ЗАДАЧИ ОПТИМИЗАЦИИ
- •5.1. Постановка задачи
- •5.2. Условия оптимальности в выпуклых задачах
- •6. МЕТОДЫ РЕШЕНИЯ ОПТИМАЛЬНОЙ ЗАДАЧИ ДЛЯ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
- •6.1. Необходимые и достаточные условия экстремума функции одной переменной
- •6.2. Алгоритм аналитического метода
- •7. ИТЕРАЦИОННЫЕ МЕТОДЫ ОПТИМИЗАЦИИ
- •7.1. Алгоритм итерационного метода
- •7.2. Метод сканирования
- •7.3. Определение унимодальной функции
- •7.4. Метод дихотомии
- •7.5. Метод золотого сечения
- •7.6. Одномерный градиент
- •7.7. Методы полиномиальной аппроксимации
- •7.8. Метод Пауэлла
- •7.9. Метод ДСК
- •7.10. Метод квадратичной интерполяции
- •7.11. Метод кубической аппроксимации
- •7.12. Метод Фибоначчи
- •7.14. Методы поиска безусловного экстремума невыпуклых функций
- •7.15. Метод тяжелого шарика
- •8. ЗАДАНИЯ
- •8.1. Исследование функции на выпуклость (вогнутость)
- •8.2. Варианты задач безусловной оптимизации
- •8.3. Варианты задач условной оптимизации
- •9. КОНТРОЛЬНЫЕ ВОПРОСЫ
- •10. ЛИТЕРАТУРА

точкам xа, xb, xc:
x* = xb + |
x[ f (xa ) − f (xc )] |
|
2[ f (xa ) −2 f (xb ) + f (xc )] |
||
|
6. Проверяем условие окончания поиска: f (x* ) − f (xm ) < ε ,
где xm – одна из точек xа, xb, xc, в которой значение целевой функции максимально;
– если условие выполняется, то считается, что поиск экстремума заканчивается и экстремум найден в точке x*;
– иначе, x = x 2 и переходим к шагу 2, причем x0 = x*.
Данная циклическая процедура будет выполняться до тех пор, пока не будут выполнены условия на 6 шаге.
7.10. Метод квадратичной интерполяции
Метод квадратичной интерполяции используют для поиска точки минимума х* непрерывной функции f(x), определенной на множестве
D ={x : a ≤ x ≤ b} . Из области допустимых значений D выделяется подмножество D1, в котором расположена точка экстремума х*, и аппроксимируется функция f(x) (х принадлежит подмножеству D1) некоторой сильно выпуклой функцией вида:
ϕ(x) = a1 x2 + a2 x + a3
Далее аналитическим методом находится точка минимума x4 функции ϕ(x) из необходимого условия существования экстремума
ϕ '(x) = 2 a1 x4 + a2 = 0. |
|
Отсюда |
|
x4 = −a2 /(2a1 ) , |
(7.16) |
которая тем ближе к точке х*, чем ближе функция ϕ(x) к f0(x) на подмно73

жестве D1.
Для нахождения множества D и коэффициентов a, b, c функции ϕ(x) необходимо подобрать вблизи предполагаемого минимума x4 точки x1, x2, x3, такие, что крайние ординаты больше средней ординаты, т.е. при x1<x2<x3 было справедливо неравенство:
f (x1 ) > f (x2 ) < f (x3 ).
По условию интерполяции значения аппроксимирующей параболы ϕ(xi) должны совпадать со значениями целевой функции f(xi), ϕ(xi) = f(xi), i = 1,2,3. В результате получается система линейных уравнений, относи-
тельно неизвестных коэффициентов ai (i =1,3):
a |
x2 |
+a |
2 |
x |
+a |
3 |
= |
f (x ) = |
f |
1 |
|||||
|
1 |
1 |
+a |
|
x |
1 |
+a |
|
f (x |
1 |
) = |
|
|||
|
a |
x 2 |
2 |
2 |
3 |
= |
2 |
f |
2 |
||||||
1 |
2 |
|
|
|
|
|
|
|
|||||||
a |
x 2 |
+a |
2 |
x |
3 |
+a |
3 |
= |
f (x |
3 |
) = |
f |
3 |
||
|
1 |
3 |
|
|
|
|
|
|
|
||||||
Далее находятся неизвестные коэффициенты по методу Крамера:
|
|
|
f |
|
x |
1 |
|
|
|
|
|
|
|
x12 |
f1 1 |
|
|
|
|
|
x12 |
x1 |
f1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
x22 |
f2 1 |
|
|
|
|
|
x22 |
x2 |
f2 |
|
|
|
|
|||
|
|
|
f2 |
x2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
f |
|
x |
1 |
|
|
|
|
|
|
|
x32 |
f3 |
|
1 |
|
|
|
|
|
x32 |
x3 |
f3 |
|
|
|
|
a1 = |
|
|
|
3 |
3 |
|
|
|
; |
a2 = |
|
|
|
|
|
|
|
|
; a3 |
= |
|
|
|
|
|
|
, |
(7.17) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
c |
|
|
|
|
|
|
c |
|
|
|
|
|
|
c |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
x2 |
x |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где |
|
|
|
|
|
|
|
|
c = |
x22 |
x2 |
1 |
. |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
x2 |
x |
1 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
С учетом соотношений (7.16) и (7.17) получается выражение для определения точки x4 непосредственно через xi, fi,(i=1,2,3):
|
x |
|
(x2 |
− x2 ) f |
+ (x2 |
− x2 ) f |
2 |
+ (x2 |
− x2 ) f |
3 |
|
|
|
||||||||||
x4 = |
|
5 |
= |
3 |
|
2 |
|
1 |
|
1 |
|
3 |
|
2 |
|
1 |
|
|
. |
(7.18) |
|||
x |
6 |
2 [(x |
− x |
2 |
) |
f |
+ (x |
− x ) |
f |
2 |
+ (x |
2 |
− x ) f |
3 |
] |
||||||||
|
|
|
|
3 |
|
|
1 |
|
1 |
3 |
|
|
|
1 |
|
|
|
|
|||||
Следует заметить, что в (7.18) знаменатель x6 должен быть отличен от нуля. Если точки x1, x2, x3, близки друг к другу, то это условие нарушается.
74

Алгоритм метода квадратичной интерполяции:
1.Вводим а, b, погрешность eps определения точки локального минимума. Вычисляем шаг h=0,2·(b–a). В качестве точки x2 берем середину отрезка [a,b], т.е. x2=(а+b)/2. Вычисляем f2=f (x2). Полагаем x1 равным x2. N=1.
2.Если оба условия N = 1 и (x1–h) ≥ a выполняются, переходим к шагу 3, иначе − к шагу 6.
3.x1 = x1 – h. Вычисляем f1 = f (x1).
4.Если условие f1 > f2 выполняется, то полагаем N = 0 (точка x1 найдена).
5.Возвращаемся на шаг 2.
6.Если условие N = 1 выполняется, то это означает, что точка x1 < x2, для которой f(x1) > f(x2) не найдена. Печать "нет x1, уменьшить a". Выход из программы;
7.N=1, x3=x2.
8.Если хотя бы одно из условий N = 1 или (x3+h) ≤ b не выполняется, то переходим к шагу 12.
9.Вычисляем x3 = x3 + h, f3 = f (x3).
10.Если условие f3 > f2 выполняется, полагаем N = 0 (т.е. точка x3
найдена).
11.Возвращаемся к шагу 8.
12.Если условие N = 1 выполняется, то печать "x3>x2 такое, что, f(x3)>f(x2) не найдено. Увеличить b." Выход из программы.
13.Увеличиваем счетчик итерации N = N + 1. Вычисляем x5 (числитель формулы (7.18)) и x6 (знаменатель формулы (7.18)).
14.Если знаменатель отличен от нуля, т.е. |x6| < eps, то полагаем R=0 и переходим к шагу 20.
x
15. Находим точку минимума параболы x4 = x5 . Вычисляем
6
f4=f(x4), R=f '(x4).
16.Если условие |R| < eps выполняется, то это означает, что точка x4 является и точкой минимума целевой функции f, поэтому полагаем x2 = x4 и переходим к шагу 20.
75
17. Производим выбор интервала, в котором лежит точка x* = arg min f (x). Для этого проверяем условие f4 < f2? Если да, то переход к шагу 18, если нет, то к шагу 21.
18.Если условие x4 < x2 выполняется, то полагаем x3 = x2, f3 = f2, иначе x1 = x2, f1 = f2.
19.x2 = x4, f2 = f4.
20.Проверяем условие выхода из цикла |R|<eps ?
–да, печать 'x*= ',x2,'min f= ',f (x2), ' f '(x2)= ',PR(x2), 'N= ',N, конец.
–нет, возврат на шаг 13.
21.Проверяем условие x4 > x2? Если условие выполняется, то полагаем x3=x2, f3=f2 и переходим на п.20, иначе, полагаем x1=x4, f1=f4 и переходим к шагу 20.
Ниже приведена программа поиска минимума функции
f = x3 – 3x2 – 9x – 10, x [2,4]
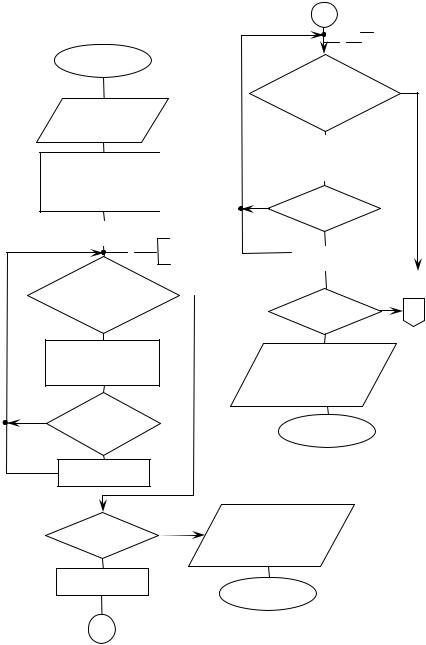
рассмотренным методом на языке Турбо-Паскаль, блок-схема алгоритма представлена на рисунке 12(а,б):
program kvadr_interp; Var
a,b,eps,x1,x2,x3,x4,x5,x6,f1,f2,f3,f4,R,h : real; N : byte;
function f(x:real):real; {функция цели} begin
f:=x*sqr(x)-3*sqr(x)-9*x-10; end;
function PR(x:real):real; {первая производная} begin
PR:=3*sqr(x)-6*x-9; end;
begin
Writeln('ввод a<b, eps'); read(a,b,eps); h:=0.2*(b-a); x2:=(a+b)/2; f2:=f(x2); x1:=x2; N:=1;
{поиск x1<x2 такого, что f(x1)>f(x2)}
76
While (N=1) and ((x1-h)>=a) Do begin
x1:=x1-h; f1:=f(x1); if f1>f2 then N:=0; end;
if N=1 then begin
Writeln('x1 не найдена, уменьшить а'); readln;
exit {выход из программы} end;
N:=1; x3:=x2;
{поиск x3>x2 такого, что f (x3)>f (x2)} While (N=1) anD ((x3+h)<=b) Do
begin
x3:=x3+h; f3:=f(x3); if f3>f2 then N:=0; end;
if N=1 then begin
Writeln('x3 не найдена, увеличить b'); readln;
exit {выход из программы} end;
repeat N:=N+1;
x5:=(sqr(x3)-sqr(x2))*f1+(sqr(x1)- sqr(x3))*f2+(sqr(x2)-sqr(x1))*f3;
x6:=2*((x3-x2)*f1+(x1-x3)*f2+(x2-x1)*f3); if abs(x6)<eps then
r:=0 {знаменатель равен нулю} else begin
{вычисление точки минимума параболы x4} x4:=x5/x6; f4:=f(x4);
r:=PR(x4);
if abs(R)<eps then x2:=x4 {точки минимума
параболы и функции совпали}
77
else begin {определение подинтервала, содержащего точку минимума функции f(x)}
if f4<f2 then begin
if f4<f2 then begin
x3:=x2; f3:=f2 end
else begin x1:=x4; f1:=f4 end;
x2:=x4; f2:=f4; end
else
if x4>x2 then begin
x3:=x2; f3:=f2; end
else begin x1:=x4; f1:=f4 end;
end;
end;
untiL abs(R)<eps; Writeln('x=',x2:15:10,'min f=',f(x2):15:10,
'Df/Dx=',pr(x2):15:10,'N=',N);
end.
Приведем результаты работы программы при различных eps:
eps |
х* |
f (х*) |
f '(х*) |
N |
1E-2 |
2,999582 |
36,999998 |
-0,005009 |
2 |
1E-4 |
3 |
-37 |
0 |
4 |
1E-6 |
3 |
-37 |
0 |
5 |
1E-8 |
3 |
-37 |
0 |
8 |
1E-9 |
3 |
-37 |
0 |
11 |
|
|
|
|
|
78
Ошибка!
Нет
Начало |
|
|
Ввод |
|
|
a,b,eps |
|
|
h=0,2*(b-a) |
|
|
|
||
x2=(a+b)/2 |
|
|
f2=f (x2) |
|
|
|
|
|
N=1, x1=x2 |
|
Поиск |
|
|
|
|
|
точки x1 |
N=1 и |
Нет |
|
(x1–h) ≥ a |
|
|
Да
x1=x1–h f1=f (x1)
f1>f2
Да
N=0
N=1 Да Нет
N=1, x3=x2
1
1
 Поиск
Поиск
точки x3 N=1 и Нет
(x3+h) ≤ b
|
|
|
Да |
|
|
|
|
|
x3=x3+h |
|
|
||
|
|
f3=f (x3) |
|
|
||
Нет |
|
|
||||
|
|
f3>f2 |
|
|
||
|
|
|
Да |
|
|
|
|
|
N=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N=1 |
Нет 2 |
|||
Да
Печать"не найдена x3, увеличить b"
Конец
Печать"не найдена x1, уменьшить
Конец
Рис.12а. Блок-схема поиска минимума методом квадратичной интерполяции
79
Ошибка!
2
N – число N=N+1, итераций
вычисление x5, x6 по (7.12)
|x6|<eps Да R=0
Нет
x4=x5 /x6 f4=f (x4) R=PR(x4)
|R|<eps |
|
|
Да |
|
|
|
|
|
|
Точки минимума параболы ϕ(x) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и функции f (x) совпали |
|
||||||
|
Нет |
|
|
|
x2=x4 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
Выбор интервала в котором |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
f4<f2 |
|
|
|
лежит точка min f |
|
x4>x2 |
Нет |
|||||||||||||||
|
|
|
|
|||||||||||||||||||
|
|
|
Нет |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Да |
|
|
|
|
|
|
|
|
|
|
|
|
|
Да |
|
||||||
|
Нет |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3=x2 |
|
|
||||||
x4<x2 |
|
x1=x2 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
f3=f2 |
|
|
||||||||||
|
|
|
|
|
|
f1=f2 |
|
|
|
|
|
|
||||||||||
|
Да |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x3=x2 f3=f2
x2=x4 f2=f4
x1=x4 f1=f4
Нет |R|<eps |
Да |
Печать |
|
'x*= ',x2,' min f= ',f(x2), |
|
|
|
'df/dx= ',PR(x2), 'N=',N |
|
|
Конец |
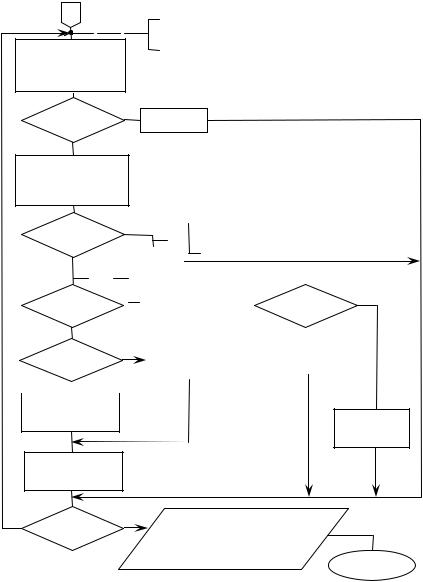
Рис.12б. Продолжение блок-схемы поиска минимума методом квадратичной интерполяции
80
