
Кузнецов_математика
.pdf
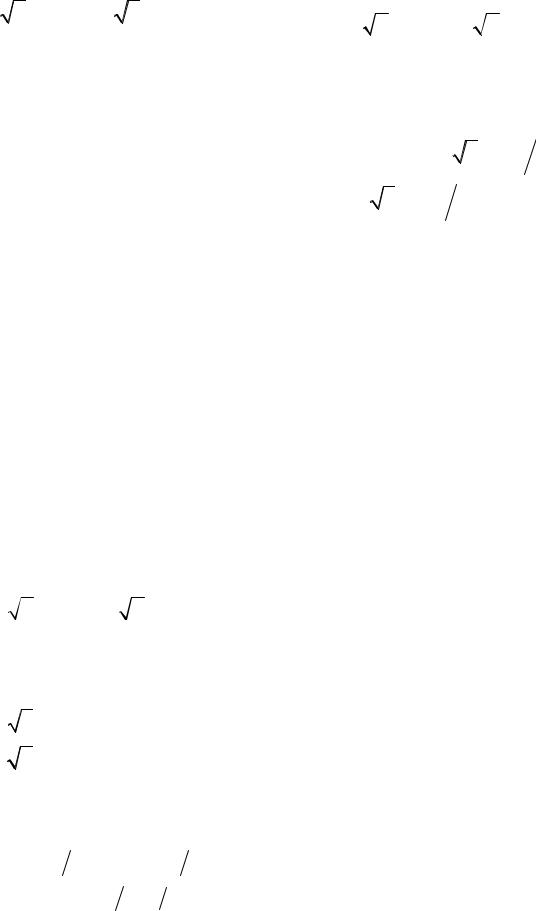

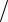

|
|
|
x − x1 |
= |
|
y − y1 |
= |
|
z − z1 |
и |
x − x2 |
= |
y − y2 |
= |
|
z − z2 |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
l1 |
|
|
m1 |
|
|
|
|
n1 |
l2 |
|
|
|
|
|
|
m2 |
n2 |
|
|
|
|
|
|
|
|
|
|||||||||||
можно записать в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
x − x1 |
|
y − y1 |
z − z1 |
|
= 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
l1 |
|
|
m1 |
|
|
n1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
l2 |
|
|
m2 |
|
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
7. |
Доказать, что |
уравнения |
прямой, |
проходящей через |
точку |
(x1, |
y1, |
z1 ) |
||||||||||||||||||||||||||||||||
параллельно |
плоскостям |
A1x + B1 y + C1z + D1 = 0 |
|
|
и |
A2 x + B2 y + C2 z + D2 = 0 |
можно |
|||||||||||||||||||||||||||||||||
записать в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
x − x1 |
|
= |
|
y − y1 |
|
= |
|
z − z1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
B1 |
C1 |
|
|
|
− |
A1 |
C1 |
|
|
|
|
A1 |
B1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
B2 |
C2 |
|
|
|
|
A2 |
C2 |
|
|
|
|
A2 |
B2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
8. Доказать, что необходимым и достаточным условием принадлежности двух |
||||||||||||||||||||||||||||||||||||||||
прямых |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x − x1 |
= |
y − y1 |
= |
z − z1 |
и |
x − x2 |
= |
y − y2 |
= |
|
z − z2 |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
l1 |
|
|
m1 |
|
|
|
|
n1 |
l2 |
|
|
|
|
|
|
m2 |
n2 |
|
|
|
|
|
|
|
|
|
|||||||||||
одной плоскости является выполнение равенства |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
x − x1 |
|
y − y1 |
z − z1 |
|
= 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
l1 |
|
|
m1 |
|
|
n1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
l2 |
|
|
m2 |
|
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
9. Доказать, что расстояние от точки A до прямой, проходящей через точку |
B и |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
имеющей направляющий вектор S, определяется формулой d = |
S, |
AB |
|
|
S |
.. |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
10. Даны две скрещивающиеся прямые, проходящие соответственно через точки |
||||||||||||||||||||||||||||||||||||||||
A(x1, |
y1, |
z1 ) и B(x2 , y2 , |
|
z2 ). Их направляющие векторы |
S1 и |
S2 известны. |
||||||||||||||||||||||||||||||||||
Доказать, что расстояние между ними определяется формулой d = |
|
|
|
|
[S1S2 ] |
|
|
|||||||||||||||||||||||||||||||||
S1S2 AB |
|
. |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Расчетные задания |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Задача 1. Написать разложение вектора x по векторам p, |
q, |
|
r. |
|
|
|
|
|
||||||||||||||||
1.1. |
x = {−2, |
4, |
7}, |
p = {0, |
1, |
2}, |
q = {1, |
|
0, |
1}, |
r = {−1, |
2, |
4}. |
|||||||||||
1.2. |
x = {6, |
12, |
−1}, |
|
p = {1, |
3, |
0}, |
|
q = {2, |
|
−1, 1}, |
|
r = {0, |
|
−1, |
2}. |
||||||||
1.3. |
x = {1, |
−4, |
4}, |
p = {2, |
1, |
−1}, |
|
q = {0, |
|
3, |
|
2}, |
r = {1, |
−1, |
1}. |
|||||||||
1.4. |
x = {−9, |
5, |
5}, |
p = {4, |
1, |
1}, |
q = {2, |
|
0, −3}, |
r = {−1, |
|
2, |
1}. |
|||||||||||
1.5. |
x = {−5, |
−5, 5}, |
|
p = {−2, |
0, |
1}, |
q = {1, |
3, |
−1} |
, |
r = {0, |
4, |
1}. |
|||||||||||
1.6. |
x = {13, |
2, |
7}, |
p = {5, |
1, |
0} |
, |
q = {2, |
|
−1, |
|
3}, |
r = {1, |
0, |
−1}. |
|||||||||
1.7. |
x = {−19, −1, |
7}, |
p = {0, |
1, |
1} |
, |
q = {−2, |
0, |
1}, |
r = {3, |
1, |
|
0}. |
|||||||||||
1.8. |
x = {3, |
−3, |
4}, |
p = {1, |
0, |
2}, |
q = {0, |
1, |
1}, |
r = {2, |
−1, |
4}. |
||||||||||||
1.9. |
x = {3, |
3, |
−1}, |
p = {3, |
1, |
0}, |
q = {−1, |
|
2, |
|
1} |
, |
r = {−1, |
|
0, |
2}. |
||||||||
1.10. |
x = {−1, |
7, |
−4}, |
|
p = {−1, |
2, |
1}, |
q = {2, |
0, |
|
3}, |
|
r = {1, |
|
1, |
−1}. |
||||||||
1.11. |
x = {6, |
5, |
−14}, |
|
p = {1, |
1, |
4}, |
|
q = {0, |
|
−3, 2}, |
|
r = {2, |
|
1, |
−1}. |
||||||||
1.12. |
x = {6, |
−1, |
7}, |
p = {1, |
−2, 0}, |
|
q = {−1, |
1, |
3}, |
|
r = {1, |
|
0, |
4}. |
||||||||||
1.13. |
x = {5, |
15, |
0}, |
p = {1, |
0, |
5}, |
q = {−1, |
|
3, |
|
2}, |
r = {0, |
−1, |
1}. |
||||||||||
1.14. |
x = {2, |
−1, |
11}, |
|
p = {1, |
1, |
0}, |
q = {0, |
1, −2}, |
r = {1, |
0, |
3}. |
||||||||||||
1.15. |
x = {11, |
5, |
−3}, |
|
p = {1, |
0, |
2}, |
|
q = {−1, |
0, |
1}, |
r = {2, |
|
5, |
−3}. |
|||||||||
1.16. |
x = {8, |
0, |
5}, p = {2, |
0, |
1}, |
q = {1, |
1, |
|
0}, |
r = {4, |
1, |
|
2}. |
|
|
|||||||||
1.17. |
x = {3, |
1, |
8}, |
p = {0, 1, 3}, |
q = {1, |
2, |
|
−1}, |
r = {2, |
0, |
−1}. |
|||||||||||||
1.18. |
x = {8, |
1, |
12} |
, |
p = {1, |
2, |
−1}, |
q = {3, |
0, |
|
2} |
, |
r = {−1, |
|
1, |
1}. |
||||||||
1.19. |
x = {−9, |
−8, |
−3}, |
p = {1, |
4, |
1} |
, |
q = {−3, |
2, |
0}, |
r = {1, |
−1, |
2}. |
|||||||||||
1.20. |
x = {−5, |
9, |
−13}, |
p = {0, |
1, |
−2}, |
q = {3, |
−1, |
1} |
, |
r = {4, |
1, |
0}. |
|||||||||||||
1.21. x = {−15, |
5, |
6}, |
p = {0, |
5, |
|
1}, |
q = {3, |
2, |
|
−1}, |
r = {−1, |
1, |
0}. |
|||||||||||||
1.22. x = {8, |
9, |
|
4}, |
p = {1, |
0, |
1}, |
q = {0, |
−2, |
1}, |
r = {1, |
3, |
|
0}. |
|
||||||||||||
1.23. x = {23, |
−14, |
−30}, |
p = { |
2, |
1, |
0}, q = {1, |
−1, |
0}, |
r = {−3, |
2, |
5}. |
|||||||||||||||
1.24. x = {3, |
1, |
3}, |
|
p = {2, 1, |
0}, |
q = {1, |
0, |
1}, |
r = {4, |
|
2, |
1}. |
|
|
||||||||||||
1.25. x = {−1, |
7, |
0}, |
p = {0, |
3, |
1}, |
q = {1, |
−1, |
2}, r = {2, |
−1, |
0}. |
||||||||||||||||
1.26. x = {11, |
−1, |
4}, |
p = {1, |
|
−1, |
|
2}, |
q = {3, |
2, |
0}, |
r = {−1, |
1, |
1}. |
|||||||||||||
1.27. x = {−13, |
2, |
18}, |
p = {1, |
1, |
|
4}, |
q = {−3, |
|
0, |
|
2}, |
r = {1, |
|
2, −1}. |
||||||||||||
1.28. x = {0, |
−8, |
9}, |
p = {0, |
−2, |
|
1}, |
q = {3, |
1, |
|
−1}, |
r = {4, |
0, |
1}. |
|||||||||||||
1.29. x = {8, |
−7, |
−13}, |
p = {0, |
1, |
5}, |
q = {3, |
−1, |
2}, |
r = {−1, |
0, |
1}. |
|||||||||||||||
1.30. x = {2, |
7, |
|
5}, |
p = {1, |
0, |
1}, |
q = |
{1, |
−2, |
|
0}, |
r = {0, |
3, |
1}. |
|
|||||||||||
1.31. x = {15, |
−20, |
−1}, |
p = |
{0, |
2, 1}, |
q = {0, |
1, |
|
−1}, |
r = {5, |
−3, |
2}. |
||||||||||||||
Задача 2. Коллинеарны ли векторы c1 и c2 , построенные по векторам a и b?
2.1. a = {1, |
−2, |
3}, |
b = {3, |
0, |
−1}, |
c1 = 2a + 4b, |
c2 = 3b − a. |
|
2.2. a = {1, |
0, |
1}, |
b = {−2, |
3, |
5}, |
c1 = a + 2b, |
c2 |
= 3a − b. |
2.3. a = {−2, |
4, |
1}, |
b = {1, |
−2, |
7}, |
c1 = 5a + 3b, |
c2 = 2a − b. |
|
2.4. a = {1, |
2, |
−3}, |
b = {2, |
−1, |
−1}, c1 = 4a + 3b, |
c2 = 8a − b. |
||
2.5. a = {3, |
5, |
4}, |
b = {5, |
9, 7}, c1 = −2a + b, |
c2 |
= 3a − 2b. |
||
2.6. a = {1, |
4, |
−2}, |
b = {1, |
1, |
−1}, |
c1 = a + b, |
c2 = 4a + 2b. |
|
2.7. a = {1, |
−2, |
5}, |
b = {3, |
−1, |
0}, |
c1 = 4a − 2b, |
c2 = b − 2a. |
|
2.8. a = {3, 4, −1}, |
b = {2, |
−1, |
|
1}, |
c1 = 6a − 3b, |
|
c2 |
= b − 2a. |
||||||
2.9. a = {−2, |
−3, |
−2}, |
b = {1, |
0, |
5}, |
|
c1 = 3a + 9b, |
c2 = −a − 3b. |
||||||
2.10. a = {−1, |
4, |
2}, |
|
b = {3, |
|
−2, |
6}, |
|
c1 = 2a − b, |
|
c2 |
= 3b − 6a. |
||
2.11. a = {5, |
0, |
−1}, |
|
b = {7, |
|
2, |
|
3}, |
c1 = 2a − b, |
c2 = 3b − 6a. |
||||
2.12. a = {0, |
3, |
−2}, |
|
b = {1, |
|
−2, |
1}, |
|
c1 = 5a − 2b, |
c2 = 3a + 5b. |
||||
2.13. a = {−2, |
7, |
−1}, |
b = {−3, |
5, |
2}, |
c1 = 2a + 3b, |
c2 = 3a + 2b. |
|||||||
2.14. a = {3, |
7, |
0}, |
b = {1, |
−3, |
|
4} |
, |
c1 = 4a − 2b, |
|
c2 |
= b − 2a. |
|||
2.15. a = {−1, |
2, |
−1}, |
b = {2, |
−7, |
1} |
, |
c1 = 6a − 2b, |
c2 = b − 3a. |
||||||
2.16. a = {7, |
9, |
−2}, |
|
b = {5, |
|
4, |
|
3}, |
c1 = 4a − b, |
c2 = 4b − a. |
||||
2.17. a = {5, |
0, |
−2}, |
|
b = {6, |
|
4, |
|
3}, |
c1 = 5a − 3b, |
|
c2 |
= 6b −10a. |
||
2.18. a = {8, |
3, |
−1}, |
|
b = {4, |
|
1, |
|
3}, |
c1 = 2a − b, |
c2 = 2b − 4a. |
||||
2.19. a = {3, |
−1, |
6}, |
|
b = {5, |
|
7, |
|
10}, |
|
c1 = 4a − 2b, |
c2 = b − 2a. |
|||
2.20. a = {1, |
−2, |
4}, |
|
b = {7, |
|
3, |
|
5}, |
c1 = 6a − 3b, |
|
c2 |
= b − 2a. |
||
2.21. a = {3, |
7, |
0}, |
b = {4, |
6, |
−1}, |
c1 = 3a + 2b, |
|
c2 |
= 5a − 7b. |
|||||
2.22. a = {2, |
−1, |
4}, |
|
b = {3, |
|
−7, |
−6}, |
c1 = 2a − 3b, |
c2 = 3a − 2b. |
|||||
2.23. a = {5, |
−1, |
−2}, |
b = {6, |
0, |
7}, |
|
c1 = 3a − 2b, |
c2 = 4b − 6a. |
||||||
2.24. a = {−9, |
5, |
3}, |
|
b = {7, |
|
1, |
|
−2}, |
|
c1 = 2a − b, |
|
c2 |
= 3a + 5b. |
|
2.25. a = {4, |
2, |
9}, |
b = {0, |
−1, |
|
3}, |
c1 = 4b − 3a, |
|
c2 |
= 4a − 3b. |
||||
2.26. a = {2, |
−1, |
6}, |
|
b = {−1, |
3, |
8}, |
|
c1 = 5a − 2b, |
c2 = 2a − 5b. |
|||||
2.27. a = {5, |
0, |
8}, |
b = {−3, |
|
1, |
|
7}, |
c1 = 3a − 4b, |
|
c2 |
=12b − 9a. |
|||


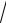 x,
x,
 2cost, y
2cost, y 
 2sint,
2sint, 4cost, y
4cost, y  4sint,
4sint, 3
3