
- •1. Неравенство Коши-Буняковского.
- •2. Неравенство треугольника.
- •3. Линейная независимость лестничной системы векторов.
- •5. Формула умножения комплексных чисел в тригонометрической форме.
- •6. Формула деления комплексных чисел в тригонометрической форме
- •7. Существование бесконечного числа решений у системы линейных однородных уравнений, в которой число неизвестных больше числа уравнений.
- •8. Теорема о пространстве решений однородной системы линейных алгебраических уравнений.
- •9. Теорема о связи общих решений неоднородной и однородной систем линейных алгебраических уравнений.
- •12. Формулы для вычисления координат вектора в ортогональном базисе.
- •13. Невырожденность ортогональной матрицы.
- •14. Изменение матрицы линейного преобразования при замене базиса.
- •15. Равенство характеристических многочленов подобных матриц.
- •16. Ортогональность собственных векторов, соответствующих различным собственным значениям самосопряженного линейного преобразования.
- •17. Изменение матрицы квадратичной формы при замене базиса.
- •14(411)Матрица перехода от базиса к базису. Преобразование координат вектора при переходе к новому базису.
- •19(416) Эллипс. Определение. Вывод канонического уравнения.
- •20(417)Гипербола. Определение. Вывод канонического уравнения.
Теоретические вопросы на доказательство:
1. Неравенство Коши-Буняковского.
Скалярным
произведением векторов х,упринадлеж.Rn:x=(x1,…,xn),
y=(y1,…yn)называется число (х,у)=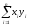
Для любых двух векторов аиb в евклидовом пространстве справедливо неравенство

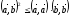
Доказательство:
Возьмем
произвольное число tи
составим вектор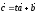
Тогда

Легко заметить
квадратный трехчлен, если
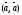 =α,
=α,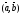 =β,
а
=β,
а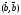 =γ,
т.е.
=γ,
т.е.
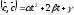
Квадратный
трехчлен
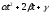 при любом значенииtнеотрицателен, поскольку
при любом значенииtнеотрицателен, поскольку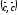 ≥0,
следовательно, дискриминант данного
трехчлена неположителен.
≥0,
следовательно, дискриминант данного
трехчлена неположителен.
D= β2- α γ≤0, подставим обратно выражения в неравенство:
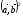 -
-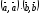 ≤0,
или
≤0,
или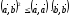 ,
чтд.
,
чтд.
Т.о., нер-во
Коши-Буняковского равносильно неравенству
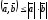
2. Неравенство треугольника.
Для любых двух векторов а иb в евклидовом пространстве справедливо соотношение, называемое неравенством треугольника:
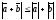 Доказательство:
Доказательство:

В силу
неравенства Коши-Буняковского, согласно
которому
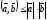 ,
,
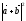
 2+2
2+2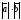 +
+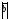 2=(
2=(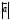 +
+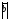 )2
)2
Извлечем корень из обеих частей этого неравенства без потери знака, т.к. обе части заведомо положительны.
Получим:
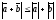
3. Линейная независимость лестничной системы векторов.
Предложение: любая лестничная система векторов линейно независима.
Доказательство:
Предположим противное. Тогда один из данных векторов должен линейно выражаться через остальные. Пусть, например, алинейно выражается черезb, c,… , то есть
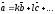
Но такое
равенство невозможно, поскольку первая
координата вектора аотлична от
нуля, а первая координата вектора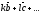 равна
нулю (из определения лестничной системы
векторов первая координата всех
последующих векторов равна нулю).
равна
нулю (из определения лестничной системы
векторов первая координата всех
последующих векторов равна нулю).
Полученное противоречие доказывает, что линейная система векторов линейно независима.
4. Однозначность разложения вектора по базису.
Предложение: Координаты вектора в данном базисе определены однозначно. Доказательство:
Допустим
,что существуют два способа разложения
вектора апо базису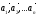
Тогда
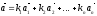
И
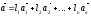
Если вычесть эти два равенства, получим, что
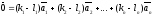
Так как векторы базиса линейно независимы, то они не равны нулю.
Значит,
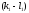 =0,
=0,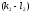 =0,
… ,
=0,
… ,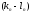 =0
=0
То есть k=l,и существует лишь один способ разложения вектора по базису.
5. Формула умножения комплексных чисел в тригонометрической форме.
Возьмем два комплексных числа в тригонометрической форме.
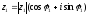
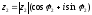 Используя
формулу умножения комплексных чисел
вида
Используя
формулу умножения комплексных чисел
вида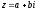
 ,
,
получим для наших двух комплексных чисел формулу:
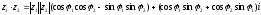 =
/используя тригонометрические формулы
косинуса и синуса суммы/
=
/используя тригонометрические формулы
косинуса и синуса суммы/
=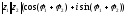
Т.о., для умножения z1наz2модули этих чисел следует перемножить, а аргументы сложить.
6. Формула деления комплексных чисел в тригонометрической форме
Возьмем два комплексных числа в тригонометрической форме.
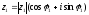
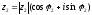 ,
гдеz2≠0.
,
гдеz2≠0.
Используя
формулу деления комплексных чисел вида
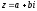
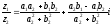 ,
,
получим для наших двух комплексных чисел формулу:
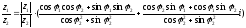 =
=
/учитывая
основное тригонометрическое тождество,
согласно которому
 =1/
=1/
= (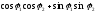 )+
(
)+
(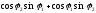 )i=
)i=
/используя тригонометрические свойства косинуса и синуса суммы и разности/
=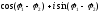
Таким образом, для нахождения частного z1/z2следует модуль числаz1 разделить на модуль числаz2, а из аргумента числаz1вычесть аргумент числаz2
7. Существование бесконечного числа решений у системы линейных однородных уравнений, в которой число неизвестных больше числа уравнений.
Однородная система, в которой число уравнений меньше числа неизвестных, всегда имеет ненулевое решение.
Запишем общий вид однородной системы mуравнений с nнеизвестными:
 а11х1+
а12х2+…+
а1nхn=0
а11х1+
а12х2+…+
а1nхn=0
а21х1+ а22х2+…+ а2nхn=0
…
аm1х1+ аm2х2+…+ аmnхn=0, гдеn>m
Применим к системе метод Гаусса.
В процессе преобразований не могут получиться противоречивые уравнения
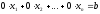 ,
гдеb≠0,
,
гдеb≠0,
т.к. все свободные члены уравнений – нули.
Значит, после некоторого числа шагов мы получаем систему, где каждому уравнению будет соответствовать свое базисное неизвестное. Но поскольку число уравнений меньше числа неизвестных, то и число базисных неизвестных должно быть меньше числа неизвестных. Следовательно, обязательно имеются свободные неизвестные, а система имеет бесчисленное множество решений.
