ТПУ Линейная алгебра 1курс ИДЗ №2

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«Национальный исследовательский Томский политехнический Университет»

Институт

дистанционного образования

линейная алгебра

Индивидуальное домашнее задание № 2

_{вариант №1}

по дисциплине:

Линейная алгебра и аналитическая геометрия

Исполнитель:
студент группы					02.12.2013
Руководитель:
преподаватель

Томск  2013

Вариант 1.

Задача 1. Даны три вектора a ={1;1;4}, b ={0;-3;2}, c ={2;1;-1}.

Требуется найти:

a) вектор , его модуль и направляющие косинусы, записать орт вектора

b) скалярное произведение векторов

c) векторное произведение векторов

d) смешанное произведение векторов

Решение:

А) По правилам выполнения арифметических операций над векторами

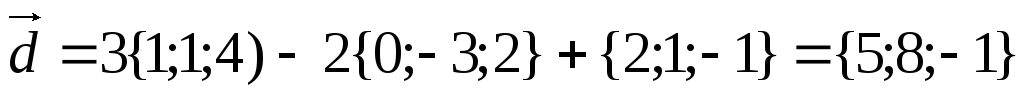
Модуль вектора

Направляющие косинусы:

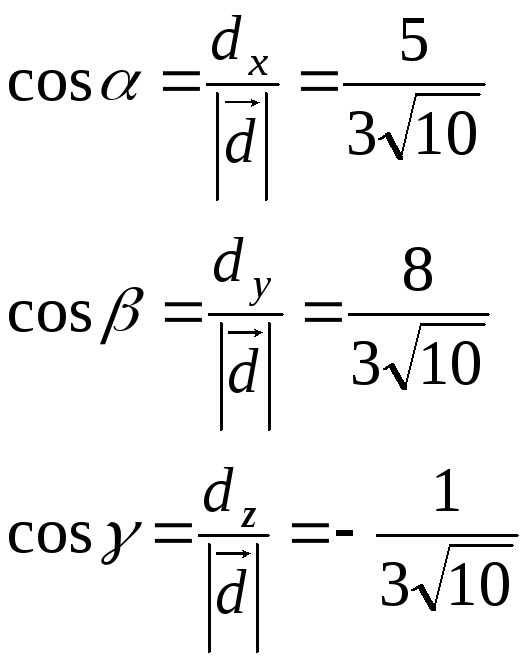
Координаты орта вектора равны отношению координат данного вектора к его модулю.

b) Сначала выполним операцию сложения векторов, а затем

скалярное умножение (сумма произведений одноименных координат)

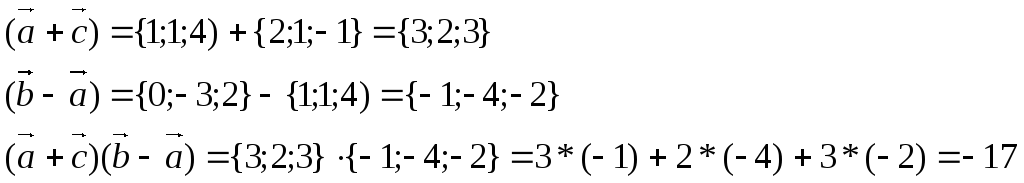
c) векторное произведение векторов находится по правилу

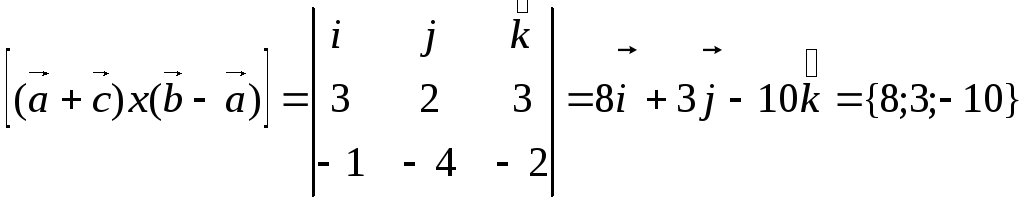
d) Произведение векторов, обозначаемое символом , есть векторно-скалярное, т.е. смешанное произведение 3-х векторов. Оно вычисляется по правилу

=

Задача 2. Определить координаты точки C на отрезке AB , если

A(2;-3;1), B(-2;2;-4) и | AC |:| CB |= 5: 2

Решение:

Обозначим координаты точки С: и составим 2 вектора

Координаты этих векторов находятся как разность соответствующих координат конечной и начальной точек. Так как все точки лежат на одной прямой, то составленные векторы являются коллинеарными и, согласно известному отношению, в котором точка делит отрезок

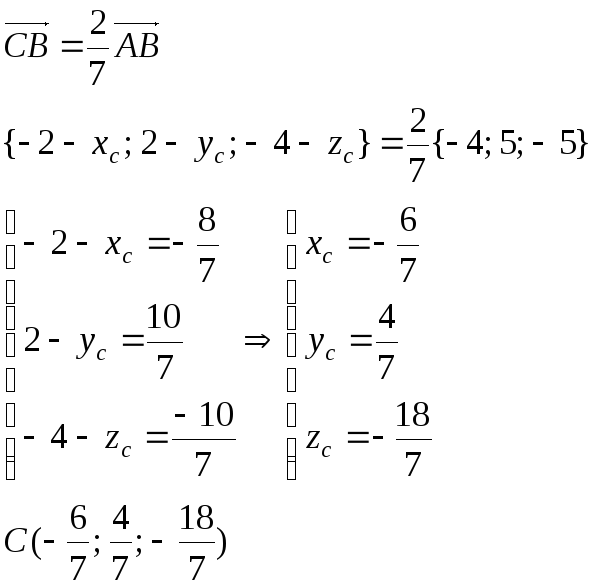
Задача 3. Найти модули векторов , если

Решение:

Так как координаты векторов не даны, для нахождения длин воспользуемся общей формулой длины вектора

Так как

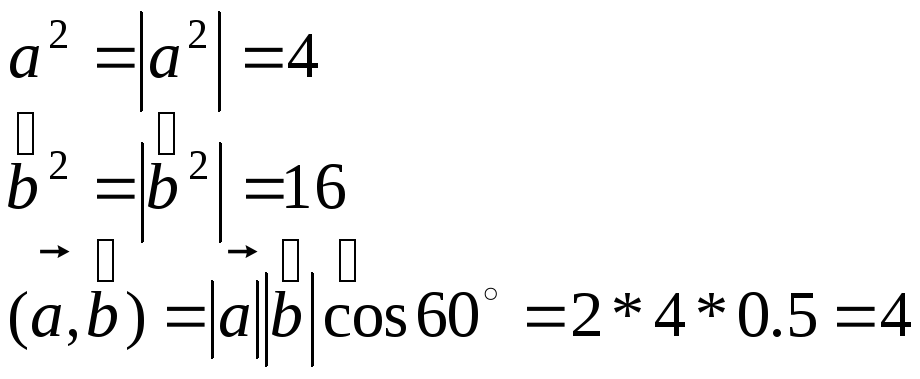
То

Задача 4. Даны три вершины параллелограмма ABCD A(3;0;-3), B(-8;2;0), C(0;3;-4) . Определить:

a) координаты четвертой вершины D ,

в) длину высоты, опущенной из вершины D на сторону AB,

с) косинус острого угла между диагоналями AC и BD .

Решение:

a) Координаты вершины D можно найти из условия равенства векторов AD и BC . Как известно, равные векторы имеют одинаковые координаты.

Координаты вектора

Координаты вектора

Таким образом

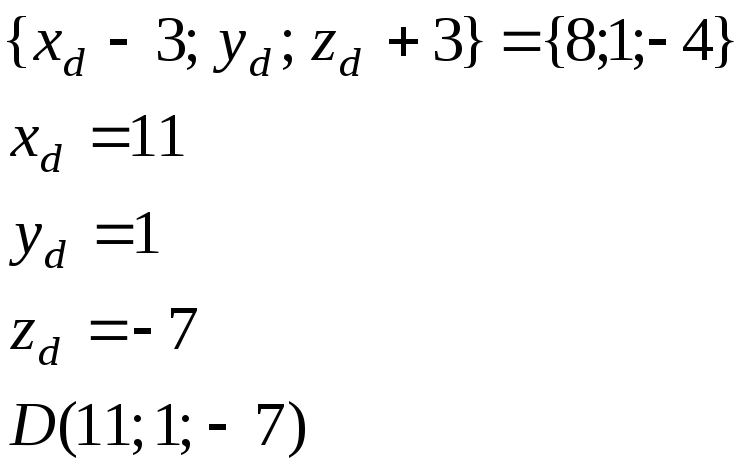
b) длину высоты найдем через площадь параллелограмма, построенного на векторах

С одной стороны

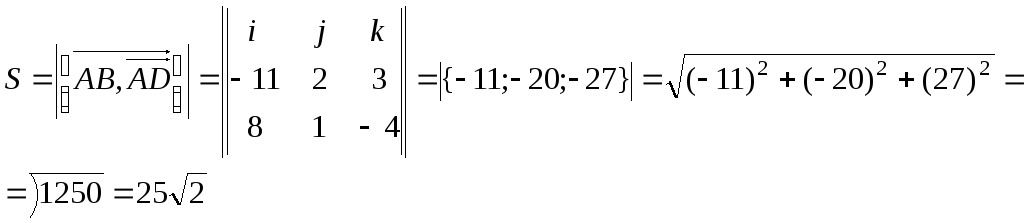
С другой стороны

Таким образом

c) Для нахождения косинуса угла между диагоналями воспользуемся формулой косинуса угла между векторами

Скалярное произведение векторов диагоналей

Так как требуется определить косинус острого угла (косинус острого угла больше нуля), то

Задача 5. Даны векторы a ={1;-2;3} и b ={5;0;-12}. Найти вектор x , если известно, что

Решение

Из условия следует, что

Из условия следует, что

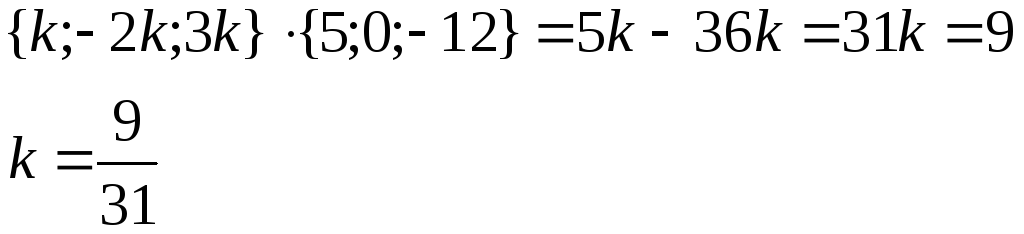
Задача 6. Найти единичный вектор x , который одновременно перпендикулярен векторам

a ={-3;-5;1} и b ={-2;6;2}, если

Решение

Так как вектор х перпендикулярен векторам а и b, значит, он параллелен нормали к этим векторам n

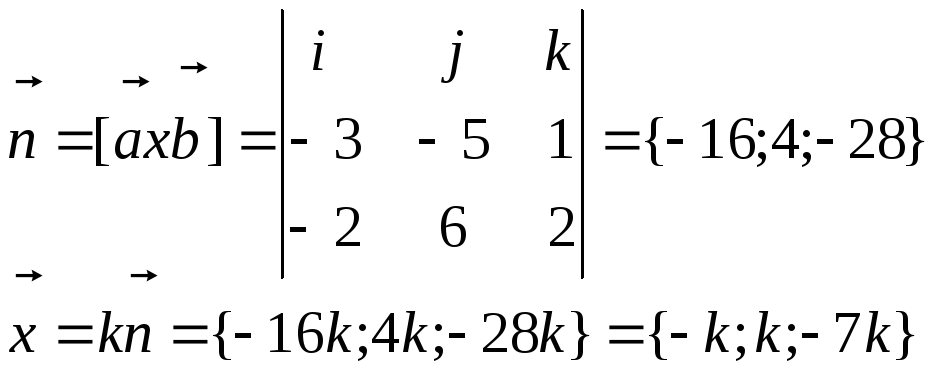
Вектор х по условию единичный, т.е.

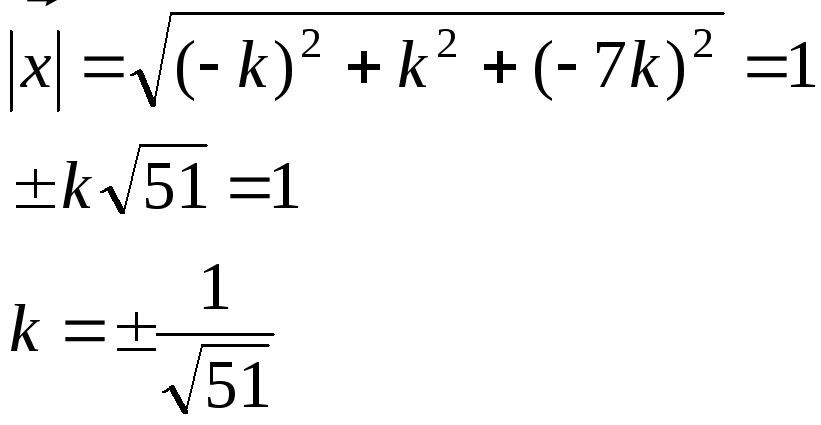
Получили 2 варианта ответа:

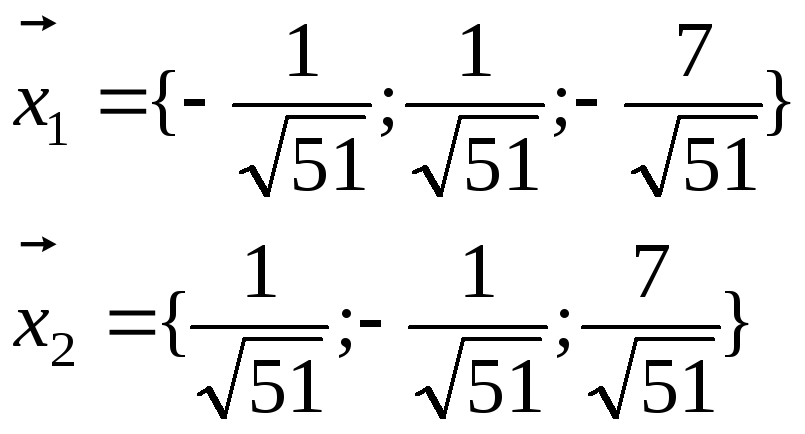
Согласно последнему условию , которое означает, что угол между искомым вектором и осью OY острый, то есть вторая координата вектора должна быть положительной, поэтому окончательным вариантом ответа есть вектор

Задача 7. В пирамиде ABCD с вершинами в точках A(1;1;1), B(-1;2;4), C(2;0;6), D(-2;5;1)

найти объем пирамиды и длину ее высоты, опущенной на грань ABC .

Решение:

Найдем векторы трех ребер пирамиды

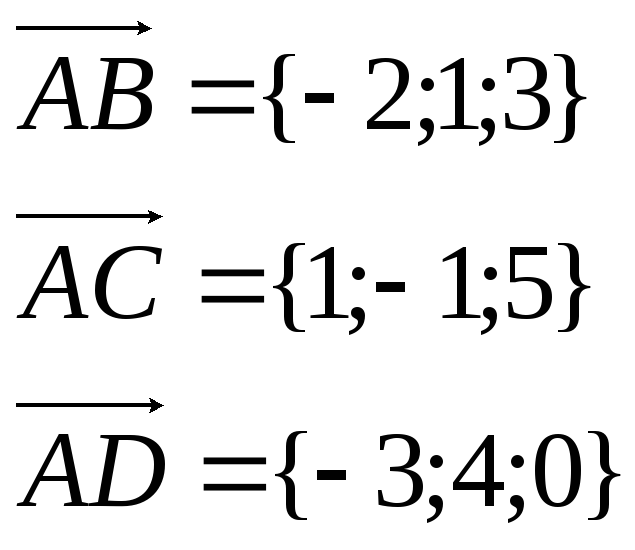
Объем пирамиды можно найти как шестая часть модуля смешанного произведения векторов ее сторон

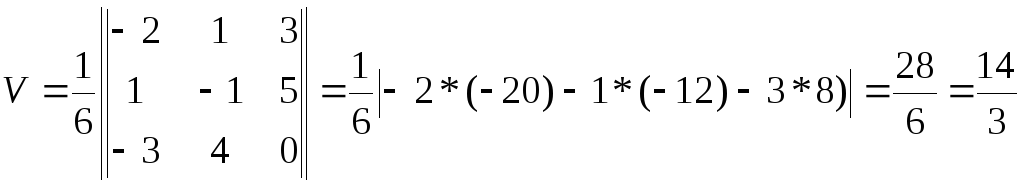
Длину высоты пирамиды, опущенной на грань ABC, можно найти

через полученное значение объема.

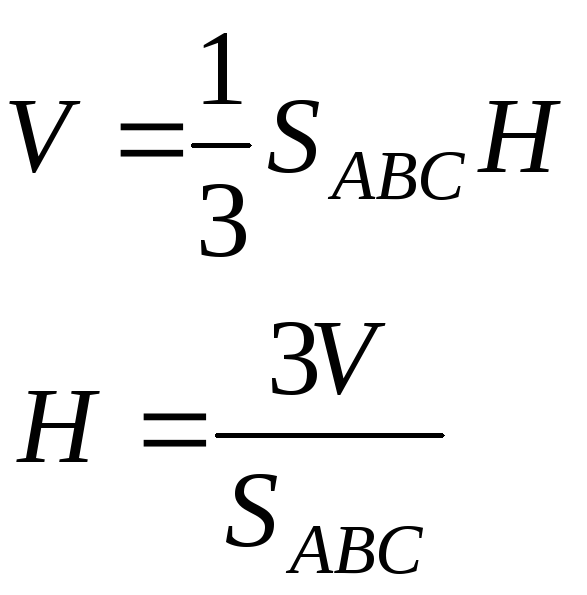
Площадь основания найдем с помощью векторного произведения

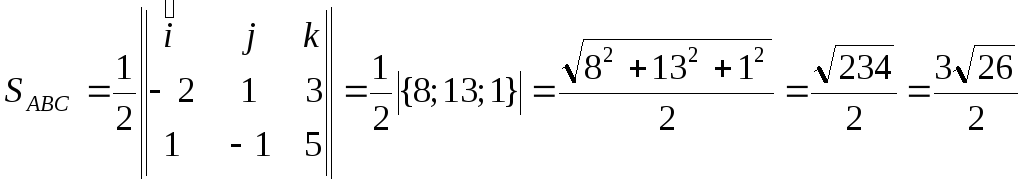
Таким образом

Задача 8. Доказать, что векторы a ={0;2;1}, b ={0;1;-1}, c ={5;-3;2} образуют базис и найти разложение вектора x ={15;-20;-1} в этом базисе.

Решение:

Для того, чтобы доказать, что три вектора в пространстве образуют базис, достаточно установить, что они некомпланарны, т.е. их смешанное произведение не равно нулю. Проверим это

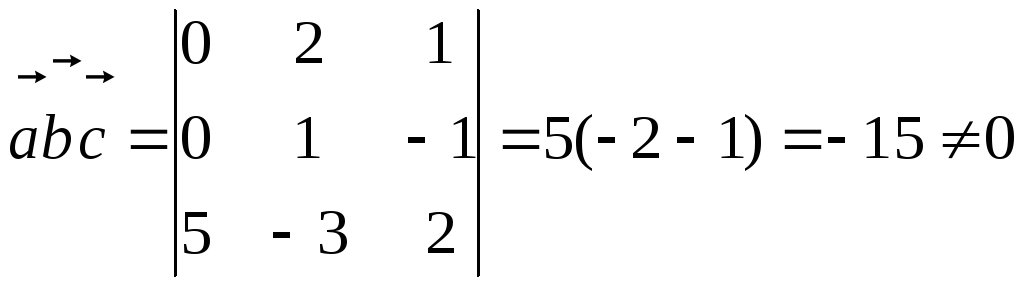
Таким образом, вектор x можно разложить в этом базисе.

Уравнивая одноименные координаты векторов, получаем систему уравнений для нахождения коэффициентов разложения.

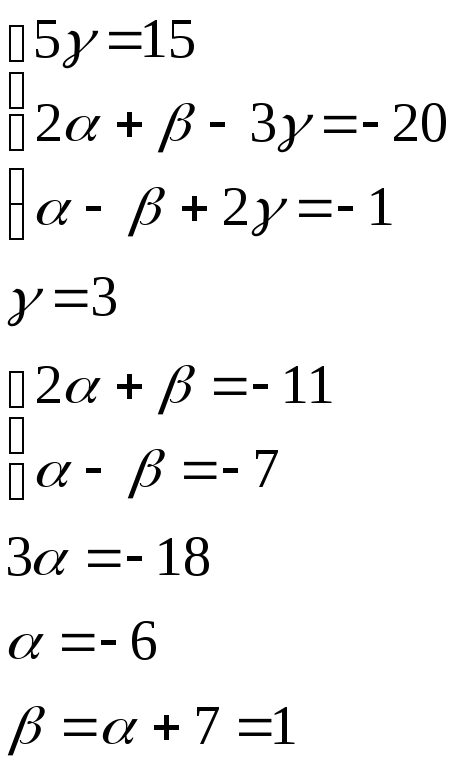
10