ТПУ Линейная алгебра 1курс ИДЗ №4

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«Национальный исследовательский Томский политехнический Университет»

Институт

дистанционного образования

140400 Элгетика и электротехника000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000

линейная алгебра

Индивидуальное домашнее задание № 4

_{вариант №1}

по дисциплине:

Линейная алгебра и аналитическая геометрия

Исполнитель:
студент группы					06.01.2014
Руководитель:
преподаватель			.

Томск ¾ 2013

Индивидуальное задание 4

Вариант 1

Задача 1. Составить уравнения плоскостей, которые проходят:

a) через точку M0 (3;-2;4) параллельно двум векторам a1 ={-3;7;1}, a2 ={2;-3;4};

b) через три точки A(1;1;2), B(2;-1;2), C(4;1;4) ;

c) через точку A(1;-5;2) перпендикулярно прямой

d) через точку M0 (2;-1;3) и отсекает на координатных осях равные

по величине и по знаку отрезки.

Решение:

a) Используем уравнение плоскости через точку M0(x0; y0; z0) с

нормальным вектором

Точка дана по условию M0 (3;-2;4), а в качестве вектора нормали можно

использовать векторное произведение векторов

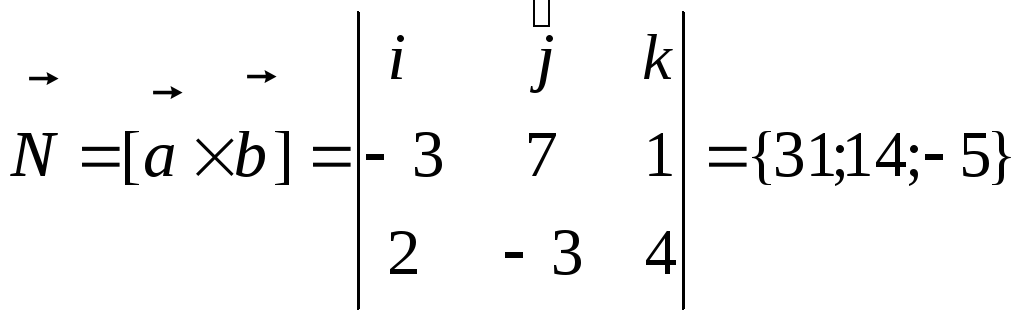
Уравнение плоскости

b) В качестве фиксированной точки берем любую из трех, например, A(1;1;2), а в качестве вектора нормали – результат векторного умножения

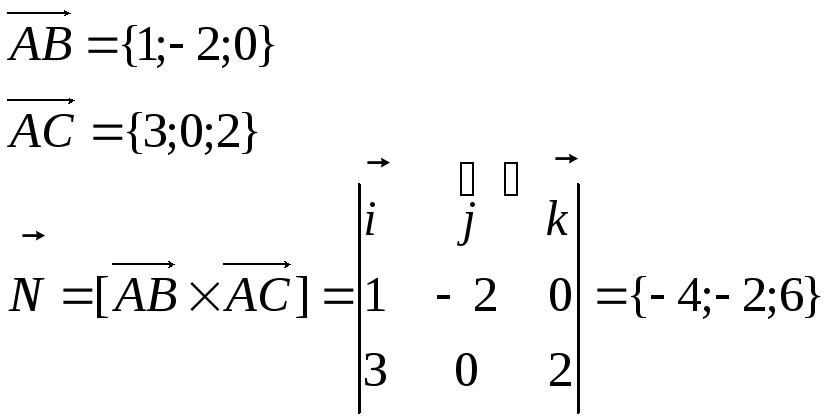
Уравнение плоскости

с) Вектором нормали может служить направляющий вектор прямой

Уравнение плоскости

d) ) через точку M0 (2;-1;3) и отсекает на координатных осях равные

по величине и по знаку отрезки.

Для того, чтобы плоскость отсекала на координатных осях равные по величине и по знаку отрезки достаточно, чтобы ее вектор нормали имел равные по знаку и величине координаты, например

Уравнение искомой плоскости будет

Задача 2. Составить канонические уравнения прямых, которые проходят:

a) через точку M0 (2;4;-5) параллельно вектору a ={3;2;-2};

b) через две точки A(1;-5;2), B(-5;1;0) ;

c) через точку M0 (2;3;-4) в направлении, которое составляет с

осями координат OX и OY углы 120 и 45 градусов соответственно;

d) через точку M0 (1;-3;-1) перпендикулярно плоскости x -5y + 2z -1= 0

Решение

а) Используя каноническое уравнение прямой , где - фиксированная точка прямой, а ее направляющий

вектор, которым в данной ситуации служит вектор a, получаем уравнение искомой прямой

b) Используем уравнение и приняв в качестве начальной точки точку А¸ получаем

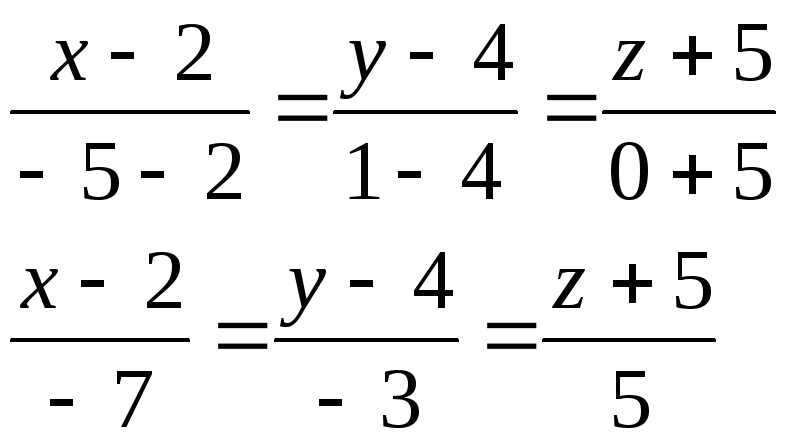
с) Найдем сначала третий угол, который данное направление составляет с осью OY . Направляющие косинусы указанного направления, которые являются координатами единичного вектора направления, удовлетворяют условию

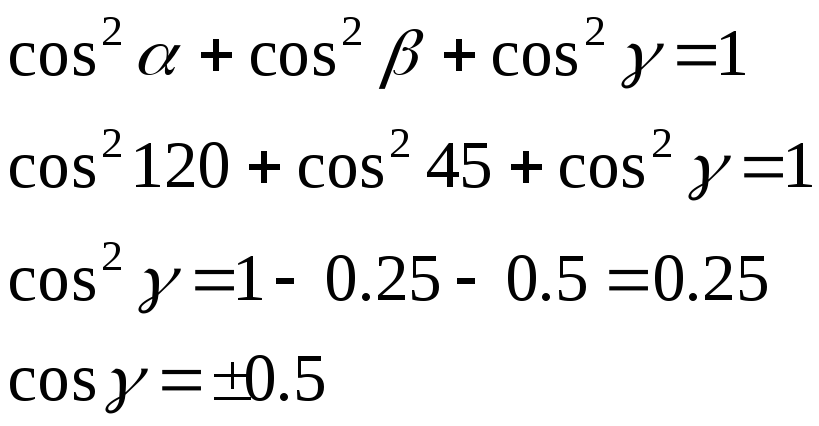
Таким образом, единичный вектор направления, который одновременно может служить и направляющим вектором прямой

Получаем две прямые (в качестве направляющего вектора прямой

возьмем удвоенный вектор

d) В этом случае нормальный вектор плоскости служит направляющим вектором прямой

Уравнение прямой

Задача 3. Из общих уравнений прямой

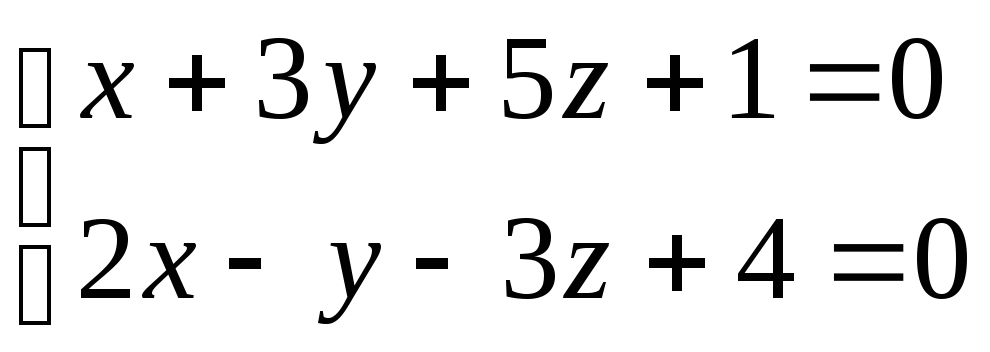
получить ее канонические и параметрические уравнения.

Решение:

Найдем на прямой конкретную точку, для чего возьмем, к примеру z = 0, и найдем остальные координаты из системы

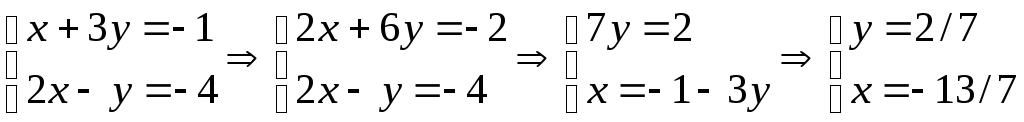
В качестве направляющего вектора берем вектор векторного произведения нормалей

плоскостей, данных в общих уравнениях прямой

Каноническое уравнение искомой прямой

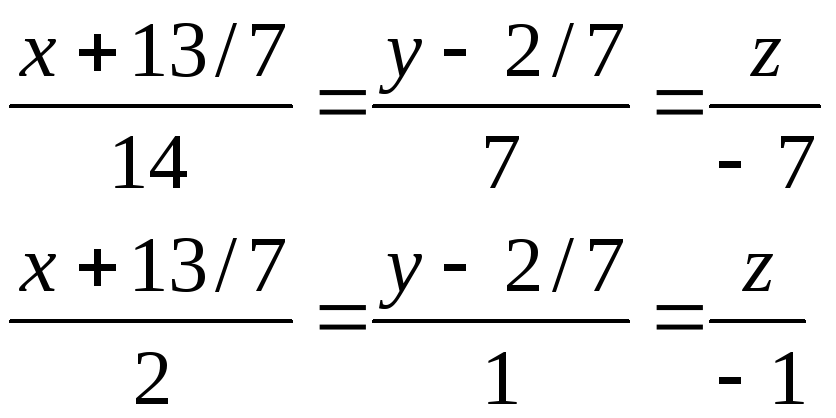
Вычислим параметрическое уравнение, введя параметр t.

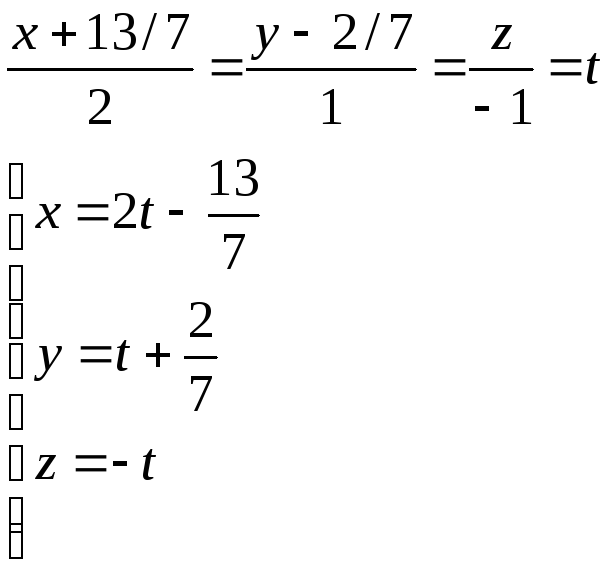
Задача 4. Найти точку пересечения и угол между прямой x = 2t +3, y = t -2, z = t +3 и плоскостью 2x -6y +14z -1= 0.

Решение:

Для нахождения точки пересечения решим систему

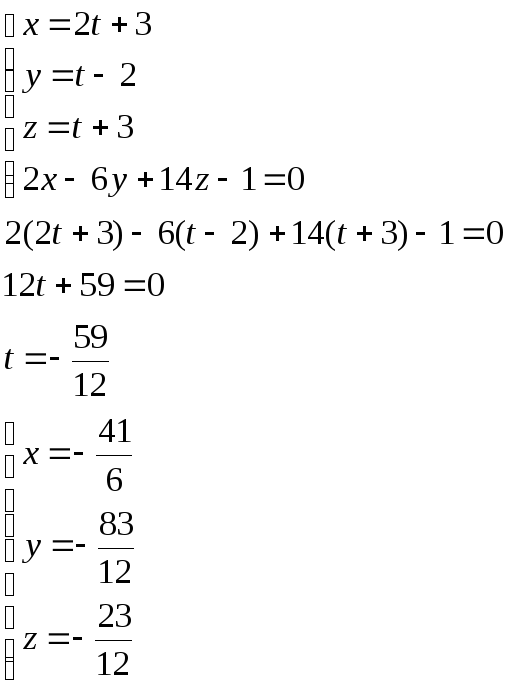
Точка пересечения

Синус угла между прямой и плоскостью равен косинусу угла между направляющим вектором прямой s ={2;1; 1} и нормальным вектором плоскости

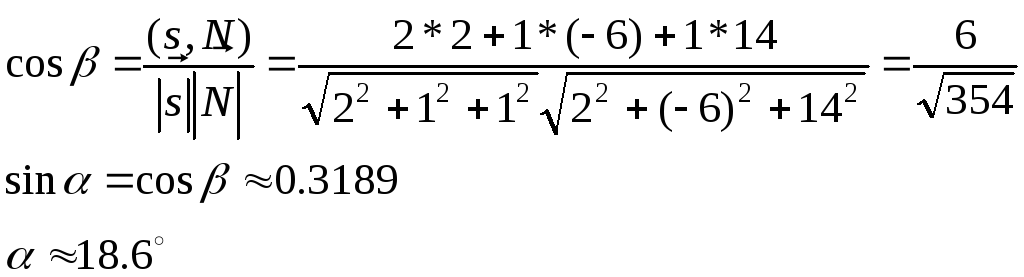
Задача 5. Определить расстояния от точки M (5;-1;0) до плоскости

3y -2z + 4 = 0 и до прямой x = 3, y = 2t + 4, z = t -2

Решение:

Расстояние от точки до плоскости определим по формуле

На данной прямой известна точка M0(3;4;-2) и ее направляющий вектор s ={0;3;1} . Расстояние d от точки M до прямой будем рассматривать как длину высоты параллелограмма, построенного на векторах M0M и s и найдем по формуле (площадь параллелограмма делится на длину основания, а площадь находим, используя векторное произведение)

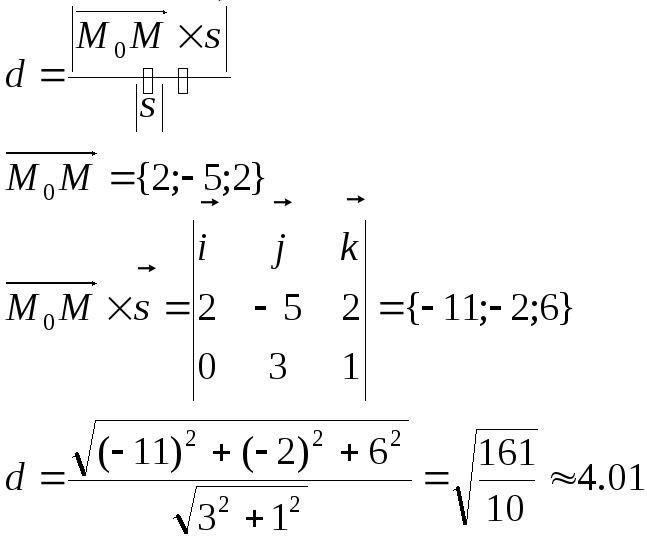
6. Построить поверхности

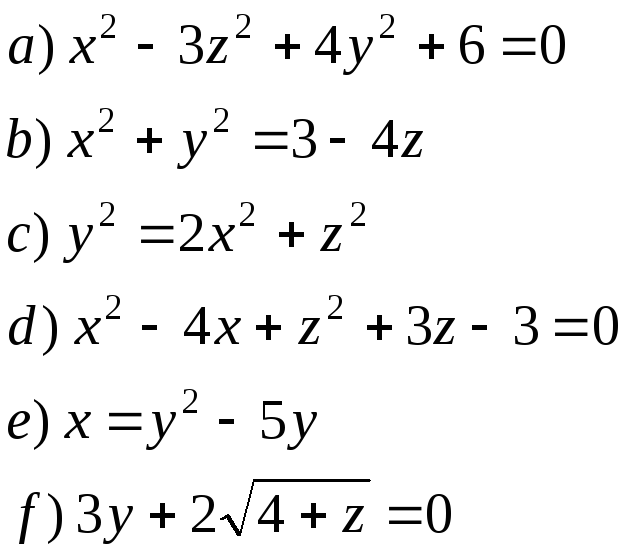
Решение

a) Преобразование уравнения состоит в переносе свободного члена 6 в правую часть уравнения, затем обе части уравнения делим на это число, чтобы получить единицу

(или -1).

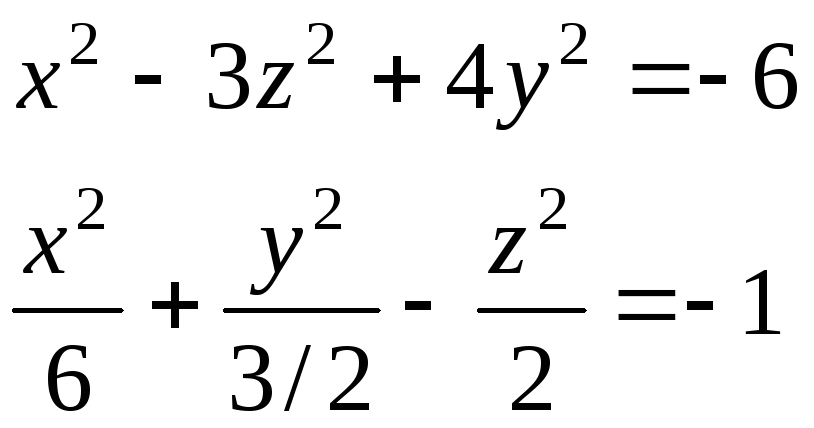
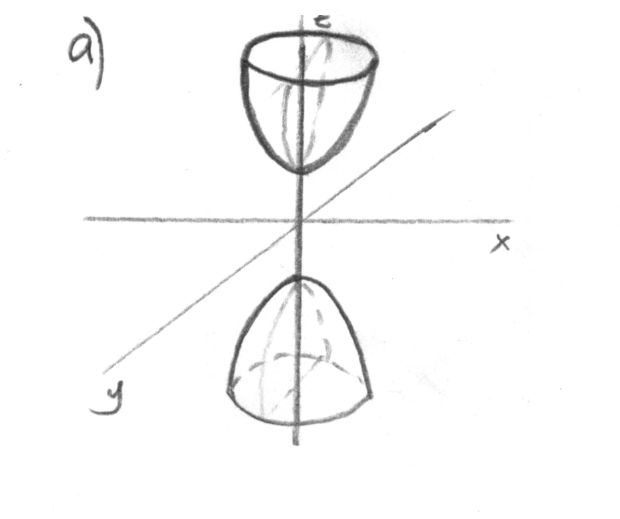
Получили каноническое уравнение двухполостного гиперболоида, осью симметрии которого служит ось OZ, так как знак «минус» в левой части уравнения стоит перед

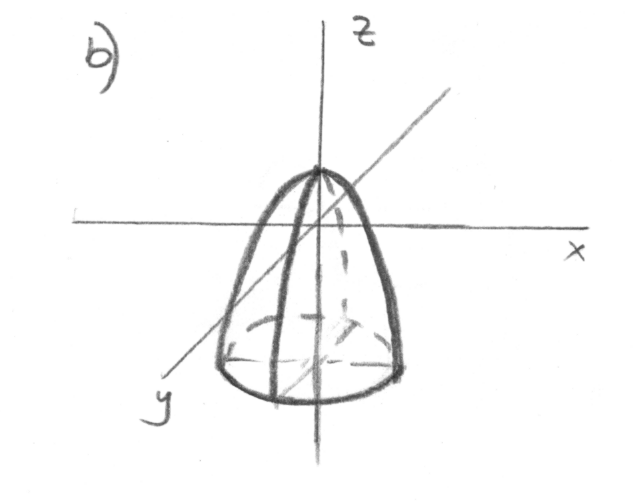
b) Выносим коэффициент -4 перед z за скобки, получаем

В уравнение переменная z входит только в первой степени, поэтому оно определяет

параболоид с вершиной в точке O1(0;0;3/4) и осью симметрии OZ, а направлен параболоид вниз, так как перед переменной z в уравнении знак «минус».

с) Переносим в правую часть уравнения и запишем его в виде:

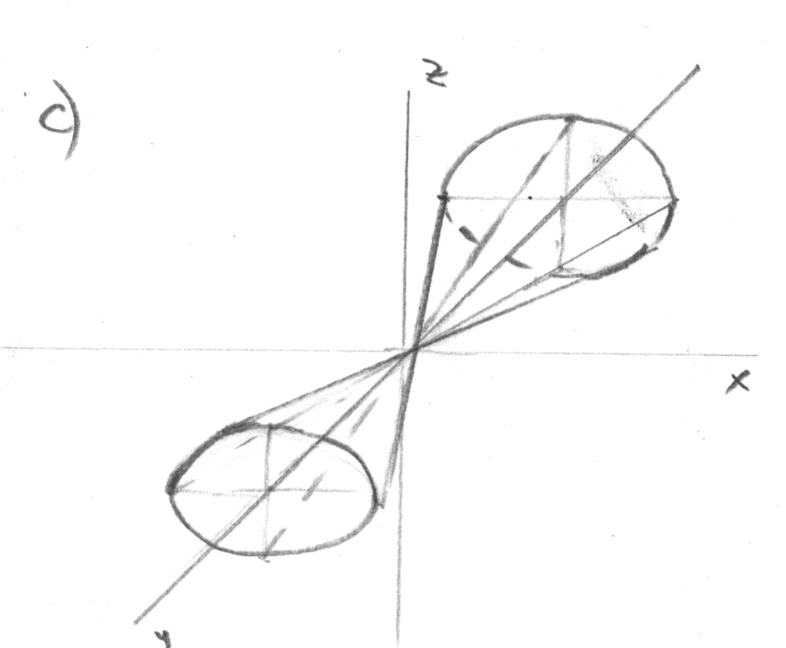
Это уравнение определяет коническую поверхность. Осью конуса служин ось ОУ, так как знак «минус» стоит перед

d)

Преобразование уравнения состоит в выделении полных квадратов для x и z. В

уравнении отсутствует переменная y , поэтому оно определяет круговой цилиндр, с образующей параллельной оси OY , а направляющей является окружность со

смещенным по осям OX и OZ центром

е)

В уравнении отсутствует переменная z , поэтому оно определяет параболический

цилиндр, образующая которого параллельна оси OZ, а направляющей является парабола со смещенной по осям OX и OY вершиной

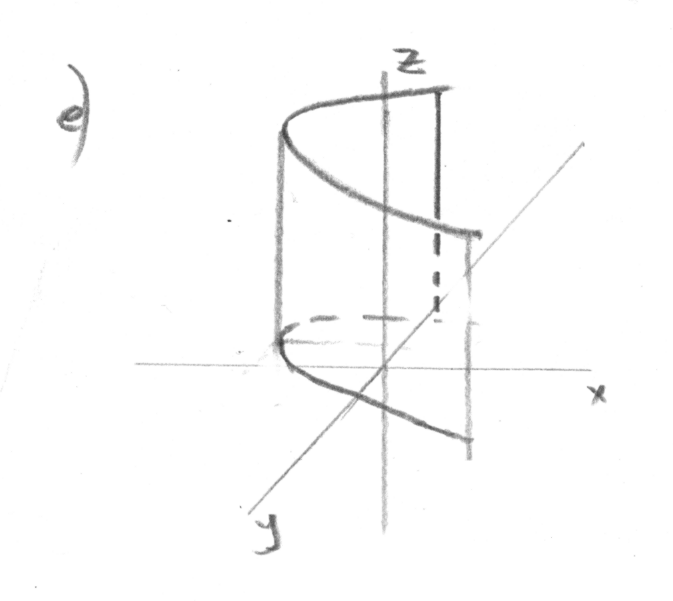
f)

Преобразованное уравнение определяет параболический цилиндр с образующей параллельной оси OX, так как в уравнении нет переменной x и вершиной смещенной на 4 единицы вниз по оси OZ.

Но по виду исходного уравнения, в котором заключаем, что оно определяет полуцилиндр (на рисунке заштрихован)

Задача 7. Построить области, ограниченные поверхностями

a)

b)

Решение:

а) Построим сначала на отдельных рисунках поверхности

Первое уравнение определяет параболический цилиндр с образующей параллельной оси OX и вершиной, смещенной на 4 единицы вверх по оси OZ.

Второе уравнение определяет параболический цилиндр с образующей, параллельной оси OZ и вершиной в начале координат

Третье уравнение определяет координатную плоскость XOY.

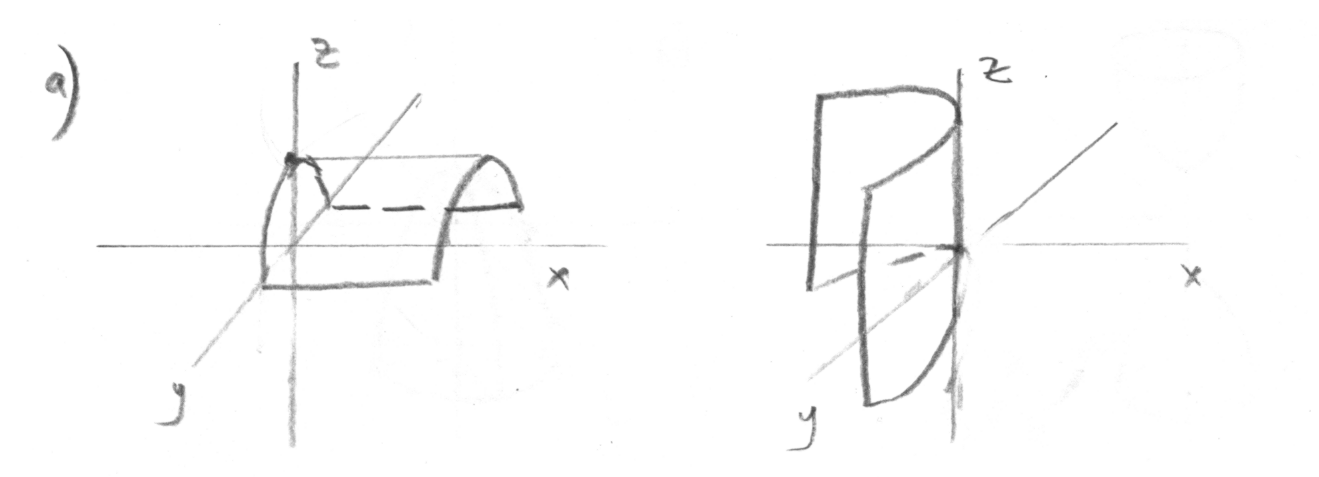
b)

В уравнение переменная х входит только в первой степени, поэтому оно определяет

параболоид с вершиной в точке O(0;0;0) и осью симметрии OX а направлен параболоид вверх.

- уравнение плоскости, параллельной координатной плоскости YOZ

12