
Кузнецов_математика
.pdf
I. ПРЕДЕЛЫ
Теоретические вопросы
1.Понятие числовой последовательности и ее предела. Теорема об ограниченности сходящейся последовательности.
2.Понятие предела функции в точке. Понятие функции, ограниченной в окрестности точки. Теорема об ограниченности функции, имеющей предел.
3.Теорема о переходе к пределу в неравенствах.
4.Теорема о пределе промежуточной функции.
5.Понятие непрерывности функции. Доказать непрерывность функции cos x.
6.Первый замечательный предел lim sin x =1.
x→0 x
7.Понятие бесконечно малой функции. Теорема о связи между функцией, ее пределом и бесконечно малой.
8.Теорема о сумме бесконечно малых функций.
9.Теорема о произведении бесконечно малой функции на ограниченную функцию.
10.Теорема об отношении бесконечно малой функции к функции, имеющей предел,
отличный от нуля.
11.Теорема о пределе суммы.
12.Теорема о пределе произведения.
13.Теорема о пределе частного.
14.Теорема о переходе к пределу под знаком непрерывной функции. 15.Непрерывность суммы, произведения и частного. 16.Непрерывность сложной функции.
17.Понятие бесконечно большой функции. Теоремы о связи бесконечно больших функций с бесконечно малыми.
18.Сравнение бесконечно малых функций.
19.Эквивалентные бесконечно малые функции. Теорема о замене бесконечно малых функций эквивалентными.
20.Условие эквивалентности бесконечно малых функций.
|
|
|
|
|
Теоретические упражнения |
||||||||||||
|
1. |
|
Доказать, что если lim a |
n |
= a, то lim |
|
a |
n |
|
= |
|
a |
|
. Вытекает ли из существования |
|||
|
|
|
|
|
|
||||||||||||
|
|
|
|
n → ∞ |
n → ∞ |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
lim |
|
a |
|
существование lim a |
n |
? |
|
|
|
|
|
|
|
|
|
|
|
n → ∞ |
|
n |
|
n → ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
У к а з а н и е. Доказать и использовать неравенство
1
|
|
|
|
b |
|
− |
|
a |
|
|
≤ |
|
b − a |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
2. |
Доказать, что последовательность {n2} расходиться. |
||||||||||||||||||
3. |
Сформулировать на языке «ε −δ » утверждение: «Число A не является пределом |
||||||||||||||||||
в точке x0 функции |
f (x), определенной в окрестности точки x0 ». |
||||||||||||||||||
4. |
Доказать, |
что если f (x) непрерывная функция, F (x) = |
|
f (x) |
|
есь также |
|||||||||||||
|
|
||||||||||||||||||
непрерывная функция. Верно ли обратное утверждение? |
|||||||||||||||||||
5. |
Сформулировать на языке «ε −δ » утверждение: «Функция f (x), определенная в |
||||||||||||||||||
окрестности точки x0 , не является непрерывной в этой точке».
6. Пусть |
lim f (x) ≠ 0, а |
lim ϕ (x) не существует. Доказать, что |
lim f (x)ϕ (x) |
|
x → x0 |
x → x0 |
x → x0 |
не существует. |
|
|
|
У к а з а н и е. Допустить противное и использовать теорему о пределе частного.
|
7. Пусть функция f (x) |
имеет предел в точке x0 , а функция ϕ (x) |
не имеет предела. |
|||||||||||||||||
Будут ли существовать пределы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1) |
lim f (x)+ϕ (x) ; |
|
2) lim |
f (x)ϕ (x)? |
|
|
|
|
|
|
|
|
||||||||
|
|
x → x |
|
|
|
|
|
x → x |
|
|
|
|
|
|
|
|
|
|
||
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||||
Рассмотреть пример: lim xsin |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
x → 0 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8. Пусть |
lim f (x) ≠ 0, а |
функция ϕ (x) |
бесконечно |
большая |
при |
x → x0 . |
|||||||||||||
|
|
|
|
|
x → x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доказать, что |
произведение |
f (x)ϕ (x) |
является |
бесконечно |
большой |
функцией |
при |
|||||||||||||
x → x0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
9. Является ли бесконечно большой при x → 0 функция |
1 |
cos |
1 |
? |
|
|
|
||||||||||||
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
x |
|
|
|
|
|
|
10.Пусть |
α′(x) α (x) |
|
и |
|
β′(x) β (x) |
при x → x . |
Доказать, |
что |
если |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
lim |
α′(x) |
не существует, то |
lim |
|
α (x) |
тоже не существует. |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
(x) |
|
β (x) |
|
|
|
|
|
|
|
|
|||||||||
x → x0 β′ |
|
|
x → x0 |
|
|
|
|
|
|
|
|
|
|
|
||||||
2

Задача 1. Доказать, что
1.1. |
a |
= |
|
3n − 2 |
, |
a = |
3 |
. |
|||||||
|
|
|
|
|
|
||||||||||
|
n |
|
|
2n −1 |
2 |
|
|
||||||||
1.3. |
a |
= |
|
7n + 4 |
, |
a = |
7 |
. |
|||||||
|
|
|
|
|
|||||||||||
|
n |
|
|
2n +1 |
2 |
|
|||||||||
1.5. |
a |
= |
|
7n −1 |
, |
a = 7. |
|||||||||
|
|
||||||||||||||
|
n |
|
|
n +1 |
|
|
|
|
|
|
|
||||
1.7. an |
= |
9−n3 |
, |
a = − |
1 |
. |
|||||||||
|
|
||||||||||||||
|
|
1+2n3 |
2 |
|
|
||||||||||
Расчетные задания
liman = a (указать N (ε )
n→∞
1.2. an =
).
4n −1, a = 2.
2n +1
1.4. a |
|
= |
2n − 5 |
, |
a = |
2 |
. |
n |
|
|
|||||
|
|
3n +1 |
3 |
|
|||
1.6. |
a = |
4n2 +1 |
|
, a= |
4 |
. |
||||
|
|
|
||||||||
n |
|
3n2 +2 |
|
3 |
||||||
1.8. |
a |
= |
4n − 3 |
, |
a = 2. |
|||||
2n +1 |
||||||||||
|
n |
|
|
|
|
|
|
|||
1.9. a = |
1−2n2 |
|
|
|
|
|
, |
a = − |
1 |
. |
|||||||||||||||||
2+4n2 |
|
|
|
||||||||||||||||||||||||
|
n |
|
|
|
|
|
|
2 |
|||||||||||||||||||
1.11. |
a |
|
= |
|
n +1 |
, |
a = − |
1 |
. |
||||||||||||||||||
n |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
1− 2n |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||
1.13. a |
= |
1−2n2 |
|
, |
|
a= −2. |
|||||||||||||||||||||
|
n2 +3 |
|
|||||||||||||||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1.15. |
a |
|
= |
|
n |
, |
|
a = |
1 |
. |
|
|
|||||||||||||||
n |
3n −1 |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|||||||
1.17. a |
|
= |
|
4 + 2n |
, |
a = − |
2 |
. |
|||||||||||||||||||
n |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
1− 3n |
|
|
|
|
3 |
|
|
||||||||||||||
|
|
|
= |
|
|
3−n2 |
|
|
|
|
|
|
a = − |
1 |
|
|
|
|
|
||||||||
1.19. an |
|
|
|
|
|
|
, |
|
|
. |
|
|
|
||||||||||||||
1+2n2 |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||
1.21. |
a |
|
= |
3n −1 |
, |
a = |
3 |
. |
|||||||||||||||||||
n |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
5n +1 |
|
5 |
|
|
|
|
|
|
|
|
|||||||||||
1.10. a |
= − |
5n |
|
|
|
, |
a = −5. |
||||||||||||
|
|
|
|
|
|
||||||||||||||
|
n |
|
|
|
|
n +1 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1.12. |
a |
= |
|
|
2n +1 |
, |
|
a = |
2 |
. |
|
||||||||
|
|
|
|
||||||||||||||||
|
n |
|
|
|
3n − 5 |
|
|
3 |
|
|
|
||||||||
1.14. an |
= |
|
3n2 |
|
|
, |
|
|
|
a = −3. |
|||||||||
2−n2 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1.16. |
a |
= |
3n3 |
|
, |
|
|
|
a =3. |
||||||||||
n3 −1 |
|
|
|
||||||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1.18. |
a |
= |
5n +15 |
, |
a = −5. |
||||||||||||||
|
|
||||||||||||||||||
|
n |
|
|
|
6 − n |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1.20. |
a |
= |
2n −1 |
, |
a = − |
2 |
. |
||||||||||||
|
|
||||||||||||||||||
|
n |
|
|
|
2 − 3n |
|
|
3 |
|
||||||||||
1.22. |
a |
= |
4n − 3 |
, |
a = 2. |
||||||||||||||
|
|||||||||||||||||||
|
n |
|
|
|
2n +1 |
|
|
|
|
|
|
|
|||||||
1.23. |
a |
= |
|
1−2n2 |
, |
a = − |
1 |
. |
1.24. |
a |
= |
|
5n +1 |
, |
a = |
1 |
. |
|
|||||||||||||
|
2+4n2 |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
n |
|
|
|
2 |
|
n |
10n − 3 |
|
2 |
|
|
|
||||||||||||||||||
1.25. a |
= |
2 − 2n |
, |
|
|
a = − |
1 |
. |
1.26. |
a |
= |
|
23− 4n |
, |
a = 4. |
||||||||||||||||
|
|
|
|
|
|
|
2 − n |
||||||||||||||||||||||||
|
n |
|
|
3+ 4n |
|
2 |
|
|
|
n |
|
|
|
|
|
|
|
|
|||||||||||||
1.27. a |
= |
1+ 3n |
, |
|
|
a = −3. |
1.28. |
a |
= |
|
2n + 3 |
, |
|
|
a = 2. |
||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||
|
n |
|
|
6 − n |
|
|
|
|
|
|
|
|
|
n |
|
|
n + 5 |
|
|
|
|
|
|
||||||||
1.29. |
a |
= |
3n2 +2 |
, |
a = |
3 |
. |
1.30. |
a |
= |
2−3n2 |
|
, |
a = − |
3 |
. |
|||||||||||||||
|
|
|
4+5n2 |
|
|||||||||||||||||||||||||||
|
n |
|
|
4n2 −1 |
|
4 |
|
|
|
|
n |
|
|
|
5 |
||||||||||||||||
1.31. |
a |
= |
2n3 |
|
, |
|
|
a = 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
n |
|
|
n3 − |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3

Задача 2. Вычислить пределы числовых последовательностей.
|
(3− n)2 + (3+ n)2 |
. |
||
2.1. lim |
− (3+ n)2 |
|||
n → ∞ (3− n)2 |
|
|||
|
(3− n)4 − (2 − n)4 |
. |
||
2.3. lim |
− (1+ n)3 |
|||
n → ∞ (1− n)3 |
|
|||
|
(6 − n)2 − (6 + n)2 |
. |
||
2.5. lim |
− (1− n)2 |
|||
n → ∞ (6 + n)2 |
|
|||
|
(1+ 2n)3 − 8n3 |
|
||
2.7. lim |
|
|
. |
|
|
|
|
||
n → ∞ (1+ 2n)2 + 4n2 |
|
|||
(3− n)3
2.9. lim .
n → ∞ (n +1)2 − (n +1)3
|
2(n +1)3 − (n − 2)3 |
|
|
||||||
2.11. lim |
|
|
|
|
. |
|
|
||
n2 + 2n − 3 |
|
|
|
|
|
||||
n → ∞ |
|
|
|
|
|
|
|
||
2.13. lim |
(n + 3)3 + (n + 4)3 |
. |
|
|
|
|
|||
|
|
|
|
|
|
|
|||
(n + 3)4 − (n + 4)4 |
|
|
|
|
|||||
n → ∞ |
|
|
|
|
|
||||
2.15. lim |
8n3 − 2n |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(n +1)4 − (n −1)4 |
|
|
|
|
|
|
|||
n → ∞ |
|
|
|
|
|
|
|
||
2.17. lim |
(2n − 3)3 − (n + 5)3 |
. |
|||||||
|
|
|
|
|
|
||||
(3n −1)3 + (2n + 3)3 |
|||||||||
n → ∞ |
|
|
|||||||
2.19. lim |
(2n +1)3 + (3n + 2)3 |
. |
|||||||
|
|
|
|
|
|
||||
(2n + 3)3 − (n − 7)3 |
|||||||||
n → ∞ |
|
|
|||||||
2.21. lim |
(2n +1)3 − (2n + 3)3 |
|
. |
||||||
|
|
|
|
|
|
|
|||
(2n +1)2 + (2n + |
3)2 |
|
|||||||
n → ∞ |
|
|
|||||||
2.23. lim |
(n + 2)4 − (n − 2)4 |
. |
|
|
|
||||
(n + 5)2 + (n − 5)2 |
|
|
|
||||||
n → ∞ |
|
|
|
|
|
||||
2.25. lim |
(n +1)3 − (n −1)3 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(n +1)2 − (n −1)2 |
|
|
|
|
|
|
|||
n → ∞ |
|
|
|
|
|
|
|
||
2.27. lim |
(n + 2)3 + (n − 2)3 |
. |
|
|
|
|
|||
n4 + 2n2 −1 |
|
|
|
|
|
|
|||
n → ∞ |
|
|
|
|
|
|
|
||
2.2. lim (3− n)4 − (2 − n)4 .
n → ∞ (1− n)4 − (1+ n)4
2.4. lim (1− n)4 − (1+ n)4 .
n → ∞ (1+ n)3 − (1− n)3
2.6. lim (n +1)3 − (n +1)2 .
n → ∞ (n −1)3 − (n +1)3
2.8. lim |
|
(3− 4n)2 |
. |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||
n → ∞ (n − 3)3 − (n + 3)3 |
|
|
|
|
|
|
|
|
|
|
|
|||
2.10. lim |
(n +1)2 + (n −1)2 − (n + 2)3 |
. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
(4 − n) |
3 |
|
|
|
|
|
|
|||||||
n → ∞ |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||
2.12. lim |
(n +1)3 + (n + 2)3 |
. |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
(n + 4)3 + (n + 5)3 |
|
|
|
|
||||||||||
n → ∞ |
|
|
|
|
|
|
||||||||
2.14. lim |
(n +1)4 − (n −1)4 |
|
. |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||
(n +1)3 + (n −1)3 |
|
|
|
|
|
|
|
|||||||
n → ∞ |
|
|
|
|
|
|
|
|
|
|
||||
2.16. lim |
(n + 6)3 − (n +1)3 |
|
|
. |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||
(2n + 3)2 + (n + 4)2 |
|
|||||||||||||
n → ∞ |
|
|
|
|
||||||||||
2.18. lim |
(n +10)2 + (3n +1)2 |
|
. |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
(n + 6)3 − (n +1)3 |
|
|
||||||||||||
n → ∞ |
|
|
|
|
||||||||||
2.20. lim |
(n + 7)3 − (n + 2)3 |
|
|
. |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
(3n + 2)2 + (4n + |
1)2 |
|
|
|||||||||||
n → ∞ |
|
|
|
|||||||||||
|
|
n3 − (n −1)3 |
|
|
|
|
|
|
|
|
|
|
|
|
2.22. lim |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
n → ∞ |
(n +1)4 − n4 |
|
|
|
|
|
|
|
|
|
|
|
||
2.24. lim |
(n +1)4 − (n −1)4 |
|
. |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||
(n +1)3 + (n −1)3 |
|
|
|
|
|
|
|
|||||||
n → ∞ |
|
|
|
|
|
|
|
|
|
|
||||
2.26. lim |
(n +1)3 − (n −1)3 |
|
|
. |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||
(n +1)2 + (n −1)2 |
|
|
|
|
|
|
|
|||||||
n → ∞ |
|
|
|
|
|
|
|
|
|
|
||||
2.28. lim |
(n +1)3 + (n −1)3 |
. |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||
n3 − 3n |
|
|
|
|
|
|
|
|
||||||
n → ∞ |
|
|
|
|
|
|
|
|
|
|
|
|||
4

2.29. lim |
(n +1)3 + (n −1)3 |
. |
2.30. lim |
(n + 2)2 − (n − 2)2 |
. |
|||||
|
|
|
(n |
+ 3) |
|
|||||
n |
3 |
+1 |
2 |
|||||||
n → ∞ |
|
n → ∞ |
|
|||||||
|
|
|
|
|
|
|||||
2.31. lim |
(2n +1)2 − (n +1)2 |
. |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||
n2 |
+ n +1 |
|
|
|
|
|
||||
n → ∞ |
|
|
|
|
|
|
||||
Задача 3. Вычислить пределы числовых последовательностей.
|
n 3 |
5n2 |
+ 4 9n8 +1 |
|||||
3.1. lim |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
||
|
|
|
|
|||||
n → ∞ (n + |
n |
) |
|
7 − n + n2 |
||||
3.3. lim 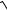
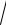 n3 +1 −
n3 +1 − 
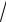 n −1. n → ∞ 3
n −1. n → ∞ 3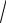 n3 +1 −
n3 +1 − 
 n −1
n −1
|
|
|
|
|
|
|
|
|
|
3n −1 − 3 |
125n3 + n |
||||
3.5. lim |
|
|
|
|
|
|
. |
|
|
|
|
|
|
||
n → ∞ |
5 |
n |
− n |
||||
|
|
|
|
||||
3.7. lim 
 n + 2 −
n + 2 − 
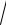 n2 + 2 .
n2 + 2 .
n→ ∞ 4 4n4 +1 − 3 n4 −1
3.9.lim 6n3 − 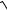
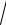 n5 +1.
n5 +1.
n→ ∞ 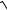
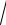 4n6 + 3 − n
4n6 + 3 − n
|
|
|
|
|
|
|
|
|
|
|
n |
4 3n +1 + 81n4 − n2 +1 |
|||||||
3.11. lim |
|
|
|
|
|
|
|
|
. |
|
(n + 3 |
|
|
) |
|
|
|||
|
|
|
|||||||
n → ∞ |
n |
5 − n + n2 |
|||||||
3.13. lim 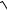
 n5 + 3 −
n5 + 3 − 
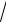 n − 3 . n → ∞ 5
n − 3 . n → ∞ 5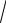 n5 + 3 +
n5 + 3 + 
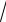 n − 3
n − 3
3.15. lim 
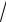 4n +1 − 3
4n +1 − 3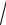 27n3 + 4 .
27n3 + 4 .
n → ∞ 4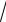 n − 3 n5 + n
n − 3 n5 + n
3 |
n3 − 7 + 3 n2 + 4 |
||||||
3.17. lim |
|
|
|
|
. |
||
|
|
|
|
|
|
||
|
|||||||
n → ∞ |
4 n5 + 5 + n |
||||||
4n2 − 4 n3
3.19. lim  .
.
n → ∞ 3 n6 + n3 +1 − 5n
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n −1 − |
n2 +1 |
|||||||||||||||
3.2. lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
n → ∞ 3 3n3 + 3 + 4 n5 +1 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
3 |
|
n2 −1 + 7n3 |
||||||||||||||||||
3.4. lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
n → ∞ 4 n12 + n +1 − n |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
5 n − 3 27n6 + n2 |
|||||||||||||||||||
3.6. lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||
(n + 4 |
|
|
|
) |
|
|
|
|
|
||||||||||||
|
|
|
|
||||||||||||||||||
n → ∞ |
n |
|
9 + n2 |
||||||||||||||||||
3.8. lim 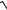
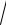 n4 + 2 +
n4 + 2 + 
 n − 2 . n → ∞ 4
n − 2 . n → ∞ 4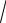 n4 + 2 +
n4 + 2 + 
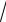 n − 2
n − 2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5n + 2 − 3 |
8n3 + 5 |
||||||||||||||
3.10. lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
n → ∞ |
4 |
|
n + 7 |
− n |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n + 3 − n2 − 3 |
|||||||||||||||
3.12. lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
n → ∞ 3 n5 − 4 − 4 n4 +1 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
3 |
n − 9n2 |
|
|
|
|
|
|
|
|||||||||
3.14. lim |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
n→ ∞ 3n − 4 9n8 +1
3.16.lim n 3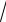 7n − 4
7n − 4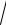 81n8 −1.
81n8 −1.
n→ ∞ (n + 4
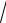 n )
n )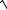
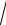 n2 − 5
n2 − 5
|
|
|
n6 + 4 + |
|
|
n − 4 |
|
||||||
3.18. lim |
|
|
|
|
|
|
|
. |
|||||
|
|
|
|
|
|
|
|
|
|||||
|
|
||||||||||||
n → ∞ 5 n6 + 6 − n − 6 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n + 3 − 3 |
8n3 + 3 |
|||||||||
3.20. lim |
|
|
|
|
. |
||||||||
|
|
|
|
|
|
|
|||||||
|
|||||||||||||
n → ∞ 4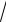 n + 4 − 5 n5 + 5
n + 4 − 5 n5 + 5
5
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 4 11n + 25n4 − 81 |
|
3 n2 − n2 + 5 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3.21. lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
3.22. lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
n → ∞ (n − 7 |
|
n |
) |
|
|
|
|
n2 − n +1 |
n → ∞ 5 n7 − n +1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
n7 + 5 − n − 5 |
|
3 n2 + 2 − 5n2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3.23. lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
3.24. lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
n → ∞ 7 n7 + 5 + n − 5 |
n → ∞ n − n4 − n +1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n + 2 − 3 |
|
n3 + 2 |
|
n 71n − |
3 64n6 + 9 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3.25. lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
3.26. lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
n → ∞ 7 n + 2 − 5 n5 + 2 |
n → ∞ (n − 3 |
n |
) |
|
|
|
11+ n2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n + 6 − n2 − 5 |
|
|
n8 + 6 − n − 6 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3.27. lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
3.28. lim |
|
|
|
|
|
|
|
|
. |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
n → ∞ 3 n3 + 3 + 4 n3 +1 |
n → ∞ 8 n8 + 6 + n − 6 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
n2 − n3 +1 |
|
|
n +1 − 3 |
n3 +1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3.29. lim |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
3.30. lim |
|
|
|
. |
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
n → ∞ 3 n6 + 2 − n |
n → ∞ 4 n +1 − 5 n5 +1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 6 n + 3 |
n10 +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
3.31. lim |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
n → ∞ (n + 4 |
n |
) |
|
3 n3 −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Задача 4. Вычислить пределы числовых последовательностей.
4.1. nlim→ ∞ n(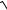
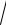 n2 +1 +
n2 +1 + 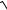
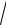 n2 −1).
n2 −1).
4.3. nlim→ ∞ (n − 3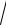 n3 − 5)n
n3 − 5)n
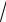 n.
n.
|
|
|
− n |
|
|
|
||
|
|
|
n(n2 + 5) |
|||||
|
|
n5 − 8 |
||||||
4.5. lim |
|
|
|
|
. |
|||
|
|
|
|
|||||
|
||||||||
n → ∞ |
|
|
n |
|||||
|
|
|
|
|||||
4.7. nlim→ ∞ (n + 3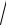 4 − n3 ).
4 − n3 ).
4.2. lim n( |
|
|
|
|
|
|
|
|
|
|
|
). |
|
|
|
|
||||
|
|
|
|
|
|
− |
|
n2 − 3 |
|
|
|
|
||||||||
|
|
|
n(n − 2) |
|
|
|
|
|||||||||||||
n → ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
( |
|
|
|
|
) |
|
|
|
|
|
|||||||||
4.4. lim |
n2 |
+1 n2 − 4 |
|
− n4 |
− 9 |
|||||||||||||||
n → ∞ |
|
|
|
)( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
− n). |
|
|
|
|
|
|
|
|||||||||
4.6. lim |
n2 − 3n + 2 |
|
|
|
|
|
|
|
||||||||||||
n → ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
. |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
4.8. lim |
|
n(n + 2) |
n2 − 2n + 3 |
|
||||||||||||||||
n → ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n → ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
( |
n + 2 |
)( |
) |
− |
( |
n |
)( |
n + 3 |
) |
||
4.9. |
lim |
|
n +1 |
|
−1 |
|
. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4.10. nlim→ ∞ n2 (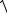
 n(n4 −1) −
n(n4 −1) − 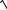
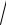 n5 − 8).
n5 − 8).
4.11. lim n(3 |
|
− 2n). |
|
(3 |
|
− 3 |
|
). |
5+ 8n3 |
4.12. lim n2 |
5+ n3 |
3+ n3 |
|||||
n → ∞ |
n → ∞ |
|
|
|
|
|
||
6
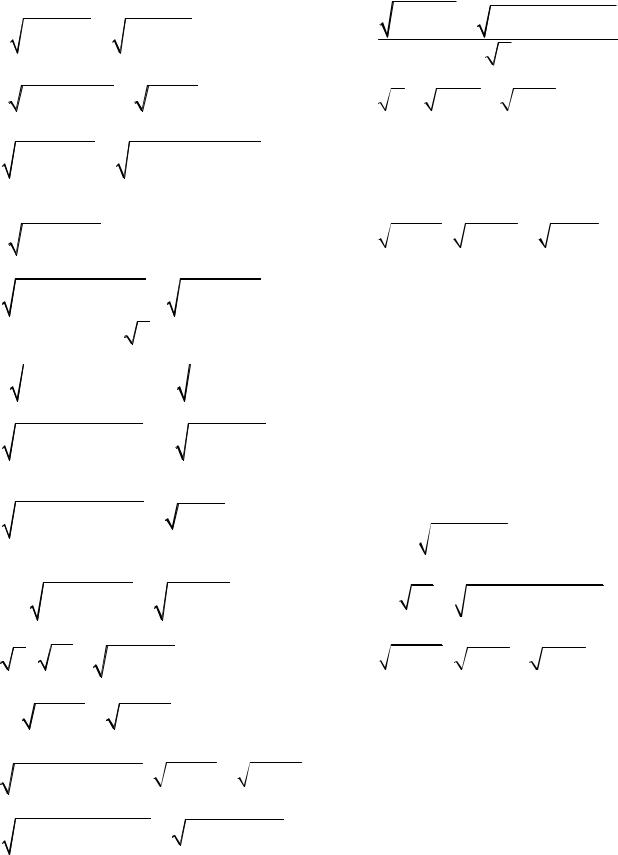
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
4.13. lim |
|
|
(n + 2)2 |
− 3 |
(n − 3)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4.14. lim |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n → ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n → ∞ |
|||
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
4.15. lim |
|
|
|
|
n2 + 3n − 2 − |
|
|
n2 − 3 |
|
|
|
|
|
|
|
|
|
|
|
|
4.16. lim |
|||||||||||||||||||||||||||||||||||||||||
n → ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n → ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
( |
n5 + |
|
|
) |
− |
( |
n4 − |
)( |
|
|
+ |
|
|
) |
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
n |
|
|
9 |
|
|
|
|
|
1 n2 |
5 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
4.17. lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
n → ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
( |
|
|
|
|
|
|
|
|
|
− n). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
4.18. lim |
|
|
|
|
n |
|
(n + 5) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.19. lim |
|||||||||||||||||||||||||||
n → ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n → ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
)( |
|
|
|
|
|
+ |
|
|
|
) |
|
− |
|
|
|
|
|
|
|
|
( |
|
|
+ |
|
|
) |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
n3 |
+1 n2 |
3 |
|
|
|
|
|
|
|
n |
|
|
n4 |
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
4.20. lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
n → ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
n → ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
( |
n2 + |
|
)( |
n2 + 2 |
) |
− |
|
|
|
( |
|
|
|
|
|
|
|
)( |
|
|
|
|
|
− 2 |
) |
||||||||||||||||||||||||||||||||
4.21. lim |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
n2 |
−1 |
|
|
|
|
n2 |
|
. |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
)( |
|
|
|
|
|
− |
) |
|
− n n |
( |
n4 + |
|
) |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
n5 |
+1 n2 |
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
4.22. lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
n → ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
)( |
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
− n6 −1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
n4 |
+1 n2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
4.23. lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
4.24. lim |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
n → ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n → ∞ |
||
n → ∞ |
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
n → ∞ |
|||||||
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
||||||||||||
4.25. lim n |
3 |
|
|
|
|
|
3 |
n |
2 |
|
|
n |
6 |
+ 4 |
|
|
|
− |
|
3 |
|
|
n |
8 |
|
−1 |
. |
|
|
|
|
|
|
|
4.26. lim |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
(3 |
|
|
− 3 |
|
|
|
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
4.27. lim 3 |
|
|
|
|
|
n2 |
|
n(n −1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.28. lim |
||||||||||||||||||||||||||||||||||||||||||||
n → ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n → ∞ |
4.29. lim n( |
|
|
|
|
|
|
|
|
|
|
|
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
n4 + 3 − |
|
n4 − 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
n → ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(n +1)3 − n(n −1)(n − 3)
.
 n
n

 n (
n (
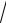 n + 2 −
n + 2 − 
 n − 3).
n − 3).
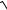
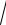 n3 + 8(
n3 + 8(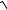
 n3 + 2 −
n3 + 2 − 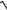
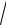 n3 −1).
n3 −1).
n − 
 n (n −1) .
n (n −1) .
n
 n −
n − 
 n (n +1)(n + 2) .
n (n +1)(n + 2) .
 n + 2(
n + 2(
 n + 3 −
n + 3 − 
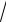 n − 4).
n − 4).
4.30. lim n(n +1)(n + 2)(
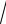 n3 − 3 −
n3 − 3 − 
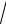 n3 − 2).
n3 − 2).
n → ∞
|
|
|
|
|
|
|
|
|
(n2 + 5)(n4 + 2) |
||||
|
|
− n6 − 3n3 + 5 |
||||
4.31. lim |
|
|
. |
|||
|
|
|||||
n → ∞ |
n |
|||||
7
Задача 5. Вычислить пределы числовых последовательностей.
|
|
1 |
2 |
|
|
3 |
|
|
|
n −1 |
|
|
( |
) |
( |
2n + 2 |
) |
! |
||||||||||||||
|
|
|
|
|
+ |
|
|
+ |
|
|
+ ...+ |
|
|
|
|
|
|
|
|
|
2n +1 !+ |
|
|
|||||||||
5.1. lim |
|
|
|
|
|
|
|
|
|
|
. |
|
|
5.2. lim |
|
|
|
|
|
|
|
|
|
. |
||||||||
|
2 |
n |
2 |
n |
2 |
n |
2 |
|
|
|
|
(2n + |
3)! |
|
|
|
||||||||||||||||
n → ∞ |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
n → ∞ |
|
|
|
|
|
||||||||||||
|
1+ 3+ 5 + 7 + ...+ |
( |
2n −1 |
2n +1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
5.3. lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
− |
. |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
n +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
n → ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2n+1 |
+ 3n+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ 2 + 3+ ...+ n |
|
|
|
|||||||||||||
5.4. lim |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
5.5. lim |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
+ 3n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
n → ∞ 2n |
|
|
|
|
|
|
|
|
|
|
|
|
|
n → ∞ |
|
9n4 +1 |
|
|
|
|||||||||||||
5.6. lim |
1+ 3+ 5 +...+ (2n −1) |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
n → ∞ |
|
|
|
1+ 2 + 3+ ..+ n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1+ 3+ 5 + 7 +...+ (2n −1) |
|
|
1+ 4 + 7 + ...+ (3n − 2) |
|||
5.7. lim |
|
− n . |
5.8. lim |
|
|
|
n + 3 |
|
|
|
|||
|
|
|
||||
n → ∞ |
|
n → ∞ |
|
5n4 + n +1 |
||
5.9. lim |
(n + 4)!− (n + 2)! |
. |
|
|
|
|
|
|
|
|
|
|
5.10. lim |
|
(3n −1)!+ (3n +1)! |
. |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
n → ∞ |
|
|
|
(n + 3)! |
|
|
|
|
|
|
|
|
|
|
|
|
n → ∞ |
|
|
|
|
|
(3n)!(n −1) |
|
|
|
|
|
|
||||||||||||||||||
|
|
2n − 5n+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ |
1 |
|
+ |
|
|
1 |
+...+ |
1 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
5.11. lim |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5.12. lim |
3 |
32 |
3n |
. |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
n → ∞ 2n+1 + 5n+2 |
|
|
|
|
|
|
|
|
|
|
|
|
n → ∞ |
1+ |
|
1 |
|
+ |
|
|
1 |
|
+...+ |
1 |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
52 |
|
5n |
||||||||||||||||
5.13. lim |
1− 3+ 5 − 7 + |
|
9 −11+ ...+ (4n − 3)− (4n −1) |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
n → ∞ |
|
|
|
|
|
|
|
|
n2 +1 + n2 + n +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
1− 2 + 3− 4 + ...+ (2n −1) |
− 2n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
5.14. lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
n → ∞ |
|
|
|
|
|
|
9n4 +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3n − 2n |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
5.15. lim |
|
3 n3 + 5 − 3n4 + 2 |
. |
|
|
|
|
5.16. lim |
|
|
|
. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2n −1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
n → ∞ 1+ 3+ 5 + ...+ ( |
|
|
|
|
|
n → ∞ 3n−1 + 2n |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
n + 2 |
− |
2 |
|
|
|
|
|
|
|
|
|
|
5 |
|
+ |
|
13 |
|
+ ...+ |
3n + 2n |
|||||||||||||||||||||||
5.17. lim |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
5.18. lim |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
+ 2 + 3+...n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
||||||||||||||||||||||||||||||
n → ∞ |
1 |
|
|
3 |
|
|
|
|
|
|
|
n → ∞ |
|
6 |
|
|
|
|
36 |
|
|
|
|
|
|
6 |
|
|
|
|
|
||||||||||||||||
5.19. lim |
2 − 5 + 4 − 7 +...+ 2n − (2n + 3) |
. 5.20. lim |
( |
2n +1)!+ (2n + 2)! |
. |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
n → ∞ |
|
|
|
|
|
|
|
|
n + 3 |
|
|
|
|
|
|
|
|
|
n → ∞ |
|
(2n + 3)!− (2n + 2)! |
||||||||||||||||||||||||||
.
.
8

|
1+ 2 +...+ n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
5.21. lim |
|
|
. |
|
|
|
|
|
|
|
|
|
5.22. lim |
|
n2 + |
|
n −1 |
|
|
. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
..+ (5n −3) |
||||||||||||
n → ∞ n − n2 + |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n → ∞ 2 + 7 +12 + |
|
||||||||||||||||||||||
|
|
|
3 |
+ |
5 |
+ |
|
9 |
|
|
+...+ |
1+ 2 |
n |
|
|
|
|
|
2 + 4 + 6 +...+ 2n |
|
|
|
|||||||||||||||||
5.23. lim |
|
|
|
|
|
. |
|
5.24. lim |
|
|
. |
|
|||||||||||||||||||||||||||
|
|
|
|
|
64 |
|
|
n |
|
|
|
+ 3+ 5 +..+ (2n −1) |
|
||||||||||||||||||||||||||
n → ∞ |
|
4 16 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
n → ∞ 1 |
|
|
||||||||||||||||||||
|
1+ 5 + 9 +13+...+ ( |
4n −3) |
− |
4n +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
5.25. lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
n → ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
5.26. lim |
1− 2 + 3− 4 +...− 2n |
. |
|
|
|
|
5.27. lim |
2n + 7n |
. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
n → ∞ |
|
|
|
|
3 n3 + 2n + 2 |
|
|
|
|
|
|
|
|
|
|
|
n → ∞ 2n − 7n−1 |
|
|
|
|
|
|
|
|
|
|||||||||||||
5.28. lim |
|
|
n!+ |
( |
n + 2 |
) |
! |
|
. |
|
|
|
|
|
|
|
5.29. lim |
3+ 6 + 9 +...+ 3n |
. |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
(n −1)!+ (n + |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
n → ∞ |
2)! |
|
|
|
|
|
|
|
|
|
n → ∞ |
|
n2 + 4 |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
7 |
|
|
|
29 |
|
|
|
|
|
|
2n + 5n |
|
|
|
|
|
2 + 4 +...+ 2n |
|
|
|
|
|
|||||||||||||||
5.30. lim |
|
|
|
|
+ |
|
|
|
|
+...+ |
|
|
|
|
|
|
. |
|
5.31. lim |
|
|
|
|
|
|
− n . |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
n + 3 |
|
|
|
|
|
|||||||||||||||||||||
n → ∞ |
|
10 |
|
|
|
100 |
|
|
|
|
|
10 |
|
|
|
|
|
|
n → ∞ |
|
|
|
|
|
|
|
|
|
|||||||||||
Задача 6. Вычислить пределы числовых последовательностей.
n +1 n |
|
|
|
||||||||||
6.1. lim |
|
|
|
|
|
. |
|
|
|
||||
|
|
|
|
|
|
|
|
||||||
n → ∞ n −1 |
|
|
|
||||||||||
|
n |
2 |
|
− |
1 |
n4 |
|
||||||
6.3. lim |
|
|
. |
|
|||||||||
|
n |
2 |
|
|
|||||||||
n → ∞ |
|
|
|
|
|
|
|
|
|||||
|
2n |
2 |
|
|
|
|
|
n2 |
|
||||
6.5. lim |
|
|
+ 2 |
|
. |
||||||||
|
2n |
2 |
|
|
|||||||||
n → ∞ |
|
+1 |
|
|
|
||||||||
|
|
2 |
|
− |
|
3n + 6 |
|
n/2 |
|||||
6.7. lim |
n |
|
|
|
. |
||||||||
|
2 |
|
+ 5n +1 |
||||||||||
n → ∞ n |
|
|
|||||||||||
|
6n − 7 3n+2 |
|
|||||||||||
6.9. lim |
|
|
|
|
|
|
|
|
. |
||||
|
|
|
|
|
|
|
|
||||||
n → ∞ 6n |
|
+ 4 |
|
|
|
||||||||
n2 + n +1 −n2
6.11. lim .
n → ∞ n2 + n −1
2n + 3 n+1
6.2. lim .
n → ∞ 2n +1
n −1 |
n+2 |
||
6.4. lim |
|
|
. |
|
|||
n → ∞ n + 3 |
|
||
|
2 |
− |
6n + 7 |
|
−n+1 |
6.6. lim |
3n |
. |
|||
2 |
+ 20n −1 |
||||
n → ∞ |
3n |
|
|||
n −10 |
3n+1 |
|
|||
6.8. lim |
|
|
. |
|
|
n +1 |
|
||||
n → ∞ |
|
|
|||
3n2 + 4n −1 2n+5
6.10. lim .
n → ∞ 3n2 + 2n + 7
2n2 + 5n + 7 n
6.12. lim .
n → ∞ 2n2 + 5n + 3
9
n −1 |
n2 |
||
6.13. lim |
|
|
. |
|
|||
n → ∞ n +1 |
|
||
|
3n +1 2n+3 |
|
|
|
|
|
|
|
||||||||
6.15. lim |
|
|
|
|
|
|
. |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||
n → ∞ |
3n −1 |
|
|
|
|
|
|
|
|
|||||||
n + 3 |
n+4 |
|
|
|
|
|
|
|
|
|||||||
6.17. lim |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
n → ∞ n + 5 |
|
|
|
|
|
|
|
|
||||||||
|
2n |
2 |
+ 21n − 7 |
|
2n+1 |
|||||||||||
6.19. lim |
|
|
. |
|||||||||||||
2n |
2 |
+18n + 9 |
|
|||||||||||||
n → ∞ |
|
|
|
|||||||||||||
|
|
3n |
2 |
|
−5n |
|
|
|
|
n+1 |
||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
6.21. lim |
|
|
|
|
|
|
|
. |
||||||||
|
2 |
|
|
|
|
|
|
|
|
|
||||||
n → ∞ |
3n − 5n + 7 |
|
|
|
|
|||||||||||
|
n |
2 |
− 6n + |
5 |
3n+2 |
|||||||||||
6.23. lim |
|
. |
||||||||||||||
|
2 |
− 5n + 5 |
||||||||||||||
n → ∞ n |
|
|
|
|
|
|
||||||||||
|
7n |
2 |
+18n −15 |
n+2 |
||||||||||||
6.25. lim |
|
. |
||||||||||||||
|
|
2 |
+11n +15 |
|||||||||||||
n → ∞ |
7n |
|
|
|||||||||||||
|
n |
3 |
+ |
n +1 |
2n2 |
|
|
|
||||||||
6.27. lim |
|
. |
|
|||||||||||||
|
|
3 |
+ 2 |
|
|
|||||||||||
n → ∞ |
|
n |
|
|
|
|
|
|
|
|
|
|||||
|
2n |
2 |
+ 2n + 3 |
|
|
3n2−7 |
||||||||||
|
|
|||||||||||||||
6.29. lim |
|
|
|
. |
||||||||||||
2n |
2 |
+ 2n +1 |
|
|||||||||||||
n → ∞ |
|
|
|
|
||||||||||||
|
|
|
2 |
+ 4n −1 |
|
1−2n |
||||||||||
6.31. lim |
4n |
. |
||||||||||||||
2 |
+ 2n + 3 |
|||||||||||||||
n → ∞ |
4n |
|
|
|
|
|||||||||||
5n2 + 3n −1 n2
6.14. lim .
n → ∞ 5n2 + 3n + 3
2n2 + 7n −1 −n2
6.16. lim .
n → ∞ 2n2 + 3n −1
n3 +1 2n−n3
6.18. lim .
n → ∞ n3 −1
10n − 3 5n
6.20. lim .
n → ∞ 10n −1
n + 3 −n2
6.22. lim . n → ∞ n +1
n + 4 n
6.24. lim .
n → ∞ n + 2
2n −1 n+1
6.26. lim .
n → ∞ 2n +1
13n + 3 n−3
6.28. lim .
n → ∞ 13n −10
n + 5 n/6+1
6.30. lim .
n → ∞ n − 7
|
Задача 7. Доказать (найти δ (ε )), что: |
|
|
|
|
|
|
|
||||
7.1. |
lim |
|
2x2 |
+ 5x − 3 |
= −7. |
7.2. lim |
|
5x2 |
− 4x −1 |
= 6. |
||
|
|
|
|
|
|
|
||||||
|
|
x + 3 |
|
|
x −1 |
|||||||
|
x → -3 |
|
x → 1 |
|
|
|||||||
7.3. |
lim |
3x2 |
+ 5x − 2 |
= −7. |
7.4. lim |
4x2 |
−14x + 6 |
=10. |
||||
|
x + 2 |
|
x − 3 |
|
||||||||
|
x → -2 |
|
x → 3 |
|
|
|||||||
10
