
Кузнецов_математика
.pdf
0,3
20.15. ∫ e−2x2 dx.
0
20.17. |
0,2∫ cos(25x2 )dx. |
||||||
|
0 |
|
|
|
|
|
|
|
0,4 |
1− e |
−x 2 |
|
|
|
|
20.19. ∫ |
|
dx. |
|||||
|
x |
||||||
|
0 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
2,5 |
|
dx |
|
|
|
|
20.21. ∫ |
|
|
|
. |
|||
|
|
|
|
|
|||
|
|
|
|
||||
|
0 |
3 125 + x3 |
|||||
20.23. 0,5∫ sin(4x2 )dx.
0
2dx
20.25.∫0 4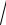 256 + x4 .
256 + x4 .
2,5 dx
20.27. ∫0 4 625 + x4 .
625 + x4 .
0,5
20.29. ∫ e−3x2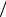 25dx.
25dx.
0
20.31. 0,1∫cos(100x2 )dx.
0
0,4
20.16. ∫ sin(5x 2)2 dx.
2)2 dx.
0
1,5 dx
20.18. ∫0 4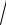 81+ x4 .
81+ x4 .
0,1 |
ln(1 |
+ 2x) |
|
|
20.20. ∫ |
dx. |
|||
|
|
|||
0 |
|
x |
||
|
|
|
||
0,4 |
|
|
|
|
20.22. ∫ e−3x2 |
4dx. |
|||
0 |
|
|
|
|
0,4 |
|
|
|
|
20.24. ∫ cos(5x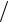 2)2 dx.
2)2 dx.
0
0,5 dx
20.26. ∫0 3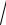 1+ x3 .
1+ x3 .
1dx
20.28.∫0 3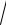 8 + x3 .
8 + x3 .
1
20.30. ∫sin x2dx.
0
28
VII. КРАТНЫЕ ИНТЕГРАЛЫ
Теоретические вопросы
1.Определение двойного и тройного интегралов. Их геометрический и физический смысл.
2.Основные свойства двойных и тройных интегралов.
3.Теорема о среднем для двойного и тройного интегралов.
4.Вычисление двойных интегралов двумя последовательными интегрированиями (случай прямоугольной области).
5.Вычисление двойных интегралов двумя последовательными интегрированиями (общий случай).
6.Замена переменных в двойном интеграле.
7.Якобиан, его геометрический смысл.
8.Двойной интеграл в полярных координатах.
9.Тройной интеграл в цилиндрических координатах.
10.Тройной интеграл в сферических координатах.
Теоретические упражнения
1. Пользуясь определением двойного интеграла, доказать, что
∫∫xm yndxdy = 0,
x2+ y2≤R2
если m и n - натуральные числа, и, по меньшей мере, одно из них нечетно. 2. С помощью теоремы о среднем найти
lim |
1 |
|
|
∫∫ |
f (x, y)dxdy, |
|
π R |
2 |
|
||||
R→0 |
2 |
2 |
≤R |
2 |
||
|
|
|
x |
+ y |
|
|
1

где f (x, y) - непрерывная функция.
3. Оценить интеграл
∫∫∫ |
|
|
dxdydz |
|
|
|
|
|
, x02 + y02 + z02 > R2 , |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
(x − x |
)2 + (y − y |
)2 |
+ (z − z |
|
)2 |
||||
x2+ y2+z2≤R2 |
0 |
|
|
||||||
|
|
0 |
0 |
|
|
|
|
|
|
т.е. указать, между какими значениями заключена его величина.
4.Вычислить двойной интеграл
∫∫f (x, y)dxdy,
D
если область D - прямоугольник {a ≤ x ≤ b, c ≤ y ≤ d }, а f (x, y) = F′′ |
(x, y). |
xy |
|
5. Доказать равенство
b d
∫∫ f (x)g(y)dxdy = ∫ f (x)dx∫g(y)dyб
D |
a |
c |
если область D - прямоугольник {a ≤ x ≤ b, c ≤ y ≤ d }.
6. Доказать формулу Дирихле
a |
x |
a |
a |
|
∫dx∫ f (x, y)dy = ∫dy∫ f (x, y)dx, |
a > 0. |
|||
0 |
0 |
0 |
y |
|
7. Пользуясь формулой Дирихле, доказать равенство
a |
y |
a |
∫dy∫ f (x)dx = ∫(a − x) f (x)dx.
0 |
0 |
0 |
8. Какой из интегралов больше
1 |
1 |
1 |
|
1 |
1−x |
1−x−y |
∫dx∫dy∫ f (x, y,z)dz |
или |
∫dx ∫ dy |
∫ f (x, y,z)dz, |
|||
0 |
0 |
0 |
|
0 |
0 |
0 |
если f (x, y,z) > 0?
2

Расчетные задания
Задача 1. Изменить порядок интегрирования.
−1 |
|
0 |
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|||||||||||||||||
1.1. ∫dy |
|
|
∫ |
|
|
|
f |
dx + ∫dy ∫ |
f |
dx. |
|||||||||||||||||||||||
−2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
− 2+ y |
|
|
|
− − y |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
2−y2 |
|
|
|
|
|
|
|||||||||
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||
1.3. ∫dy∫ f |
|
|
dx + ∫ dy |
|
∫ |
|
|
|
|
|
f |
dx. |
|||||||||||||||||||||
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
1 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||
−1 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|||||||
1.5. |
∫ |
dx |
|
∫ |
|
|
f dy + ∫dx∫ f dy. |
||||||||||||||||||||||||||
− |
|
2 |
|
|
|
− |
|
2−x |
2 |
|
|
|
|
|
|
−1 |
|
|
|
|
|
x |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
−1 |
|
|
2+ y |
|
|
0 |
|
|
|
|
|
− y |
|
|
|
|
|
|
|||||||||||||||
1.7. ∫dy |
|
∫ |
|
|
f |
|
dx + ∫dy ∫ |
f |
dx. |
||||||||||||||||||||||||
−2 |
|
0 |
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
0 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
−1 |
|
|
|
|
2−x2 |
|
|
|
|
|
|
|
0 |
|
|
|
|
x2 |
|
|
|
|
|||||||||||
1.9. |
∫ |
dx |
∫ |
f |
dy + ∫dx∫ f |
|
dy. |
||||||||||||||||||||||||||
− |
|
2 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
−1 |
0 |
|
|
|
|
|
||||||||||
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
e |
|
|
|
1 |
|
|
|
|
|
|
|
||||||||
1.11. ∫dx ∫ |
|
|
f |
|
dy + ∫dx |
|
|
∫ |
f |
dy. |
|||||||||||||||||||||||
|
0 |
|
|
|
1−x2 |
|
|
1 |
|
|
|
ln x |
|
|
|
|
|
|
|||||||||||||||
|
π 4 |
|
|
sin y |
|
|
|
|
|
|
π 2 |
|
|
|
cos y |
|
|
|
|
||||||||||||||
1.13. |
∫ dy ∫ |
f |
dx + ∫ dy ∫ |
f |
dx.. |
||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
π 4 |
|
|
|
|
|
0 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
|
|
|
|
y |
|
|
|
|
|
|
|
e |
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||
1.15. ∫dy ∫ |
|
f |
dx + ∫dy ∫ |
|
|
|
f |
dx. |
|
|
|||||||||||||||||||||||
|
0 |
|
|
|
0 |
|
|
|
|
|
|
1 |
|
|
ln y |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1 |
|
|
|
0 |
|
|
|
|
|
|
2 |
|
|
|
|
0 |
|
|
|
|
|
|
||||||||||
1.17. ∫dy ∫ |
|
f |
dx + ∫ dy |
|
|
|
∫ |
|
|
f |
dx. |
||||||||||||||||||||||
|
0 |
|
|
|
− y |
|
|
|
|
|
1 |
|
|
− |
|
|
|
2− y2 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
3 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
0 |
|
|
||||||||
1.19. ∫ dx |
|
|
|
∫ |
|
|
f dy + ∫ dx |
|
∫ |
|
f dy. |
||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
4−x2 −2 |
|
|
|
|
|
3 |
|
|
− 4−x2 |
||||||||||||||||||
1 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
2 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|||
1.2. ∫dy ∫ |
|
f |
|
dx + ∫ dy ∫ |
|
|
|
f |
dx. |
||||||||||||||||||||||
0 |
|
|
|
− |
|
|
y |
|
|
|
|
|
|
|
1 |
|
− |
|
|
− y |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
y |
|
|
|
|
|
|
|
2 |
|
2−y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1.4. ∫dy ∫ |
f |
dx + ∫dy |
|
∫ |
|
|
|
f |
|
|
|
dx. |
|
||||||||||||||||||
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1 |
2 |
|
|
arcsin y |
|
|
1 |
|
|
|
|
|
|
|
|
|
arccos y |
||||||||||||||
1.6. |
∫ |
dy |
|
∫ |
|
|
|
f dx + ∫ |
|
|
|
dy |
∫ |
f dx. |
|||||||||||||||||
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
0 |
|
||||||
1 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
e |
|
−ln y |
|
|
|
|
|
|
|
|
|
|||||
1.8. ∫dy ∫ |
|
f |
|
dx + ∫dy ∫ |
|
|
|
f |
|
dx. |
|
||||||||||||||||||||
0 |
|
|
|
− |
|
|
y |
|
|
|
|
|
|
|
1 |
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
3 |
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|||||
1.10. |
∫ dx |
|
|
|
|
∫ |
|
fdy + ∫ |
|
|
dx |
|
|
|
∫ |
fdy. |
|||||||||||||||
|
−2 |
|
|
− 4−x |
2 |
|
− 3 |
|
|
|
|
|
|
|
|
|
4−x |
2 |
−2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1 |
|
|
|
3 y |
|
|
|
|
|
|
|
2 |
|
2−y |
|
|
|
|
|
|
|
|
|
|||||||
1.12. ∫dy ∫ |
|
f |
|
dx + ∫dy ∫ |
|
|
|
f |
|
|
|
dx. |
|
||||||||||||||||||
|
0 |
|
|
0 |
|
|
|
|
|
|
|
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
−1 |
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
||||||||
1.14. ∫dx |
|
∫ |
|
f |
dy + ∫dx ∫ |
|
|
f |
dy. |
||||||||||||||||||||||
|
−2 |
|
|
( |
2+x |
) |
|
|
−1 |
|
|
|
|
x |
|
|
|
|
|
|
|||||||||||
|
|
|
− |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
|
|
|
0 |
|
|
|
|
|
|
2 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||||||
1.16. ∫dy ∫ |
f dx + ∫dy |
|
|
∫ |
|
|
|
|
|
f |
|
dx. |
|||||||||||||||||||
|
0 |
|
|
− |
|
y |
|
|
|
|
1 |
|
− |
|
|
|
2− y |
|
|
|
|||||||||||
|
1 |
|
|
|
y2 |
|
|
|
|
|
|
|
2 |
|
2− y |
|
|
|
|
|
|
|
|
|
|||||||
1.18. ∫dy ∫ f |
|
dx + ∫dy ∫ |
|
|
|
f |
|
|
|
dx. |
|
||||||||||||||||||||
|
0 |
|
|
0 |
|
|
|
|
|
|
|
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
−1 |
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|||||
1.20. ∫dy |
|
∫ |
|
|
f |
dx + ∫dy ∫ |
|
|
f |
dx. |
|||||||||||||||||||||
|
−2 |
|
|
−(2+ y) |
|
|
−1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
3 y |
|
|
|
||||||||||||||||||||
3

|
1 |
|
|
y |
|
|
e |
1 |
|
|
|
|
|
|
|
|||
1.21. ∫dy∫ f |
dx + ∫dy ∫ |
f |
dx. |
|
|
|||||||||||||
|
0 |
|
|
0 |
|
|
|
1 |
|
ln y |
|
|
|
|
|
|
|
|
|
π 4 |
|
sin x |
|
|
π 2 |
|
cos x |
|
|
||||||||
1.23. |
∫ dx ∫ |
f dy + ∫ dx ∫ f |
dy. |
|||||||||||||||
|
0 |
|
|
0 |
|
|
|
π 4 |
|
|
0 |
|
|
|
|
|||
|
1 |
|
|
x2 |
|
2 |
|
2−x |
|
|
|
|
|
|||||
1.25. ∫dx∫ f |
dy + ∫dx ∫ |
|
f |
dy. |
||||||||||||||
|
0 |
|
|
0 |
|
|
1 |
|
0 |
|
|
|
|
|
|
|
||
|
1 |
|
|
0 |
|
|
2 |
|
0 |
|
|
|
|
|
||||
1.27. ∫dx ∫ |
f |
dy + ∫dx |
∫ |
|
|
f |
dy. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
− x |
|
1 |
− |
|
2−x |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
2− y2 |
|
|
||||
|
|
|
|
|
y |
|
|
|
|
|
|
|
||||||
|
1 |
|
|
|
|
2 |
|
|
|
|||||||||
1.29. ∫dy ∫ |
f |
dx + ∫ dy |
|
∫ |
|
|
f |
dx. |
||||||||||
|
0 |
|
|
0 |
|
|
1 |
|
0 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
4−x2 |
|
|
|
|
|
2− 4−x2 |
|||||
|
− 3 |
|
|
0 |
|
|
|
|
||||||||||
1.31. |
∫ dx |
∫ |
|
f dy + ∫ |
|
dx |
∫ f dy. |
|||||||||||
|
−2 |
|
|
|
0 |
|
|
|
− |
3 |
|
|
|
|
0 |
|
||
Задача 2. Вычислить.
∫∫(12x2 y2 +16x3 y3 )dxdy;
2.1.D
D: x =1, y = x2 , y = −
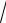 x.
x.
∫∫(36x2 y2 − 96x3 y3 )dxdy;
2.3.D
D: x =1, y = 3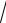 x, y = −x3.
x, y = −x3.
∫∫(27x2 y2 + 48x3 y3 )dxdy;
2.5.D
D : x =1, y = x2 , y = −3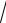 x.
x.
1 |
|
|
|
x2 |
|
|
|
|
|
|
|
2 |
|
2−x2 |
|
|
|
|
|
||||||||
1.22. ∫dx∫ f |
|
|
dy + ∫ dx |
|
∫ |
f |
dy. |
|
|||||||||||||||||||
0 |
|
|
|
0 |
|
|
|
|
|
|
|
1 |
|
|
0 |
|
|
|
|
|
|
|
|||||
−1 |
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
||||||||
1.24. ∫ |
|
dy |
|
∫ |
|
|
|
f dx + ∫dy ∫ f |
dx. |
||||||||||||||||||
− |
2 |
|
− |
|
2−y |
2 |
|
|
|
|
|
|
|
|
−1 |
|
|
y |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
2− 4−x2 |
|
|
|
|
|
|
|
|
|
|
|
4−x2 |
|
||||||||||
3 |
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||||||||
1.26. ∫ dx |
∫ |
|
|
|
f |
dy + ∫ dx |
|
|
∫ f |
dy. |
|||||||||||||||||
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2−x2 |
|
|
|
|
|
||||
1 |
|
|
|
x |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||
1.28. ∫dx∫ f |
|
dy + ∫ dx |
∫ |
f |
dy . |
|
|||||||||||||||||||||
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
1 |
|
|
|
0 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1 |
|
|
|
|
x |
|
|
|
|
|
|
2 |
|
|
2−x |
|
|
|
|
|
|||||||
1.30. ∫dx ∫ f |
dy + ∫dx |
∫ f |
|
|
dy. |
|
|||||||||||||||||||||
0 |
|
|
|
0 |
|
|
|
|
|
|
|
1 |
|
|
0 |
|
|
|
|
|
|
|
|
||||
∫∫(9x2 y2 + 48x3 y3 )dxdy;
2.2.D
D: x =1, y = 
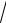 x, y = −x2.
x, y = −x2.
∫∫(18x2 y2 + 32x3 y3 )dxdy;
2.4.D
D : x =1, y = x3, y = −3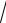 x.
x.
∫∫(18x2 y2 + 32x3 y3 )dxdy;
2.6.D
D: x =1, y = 3 x, y = −x2.
x, y = −x2.
4

∫∫(18x2 y2 + 32x3 y3 )dxdy;
2.7.D
D : x =1, y = x3, y = −
 x.
x.
∫∫(4xy + 3x2 y2 )dxdy;
2.9.D
D: x =1, y = x2 , y = −
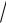 x.
x.
∫∫(8xy + 9x2 y2 )dxdy;
2.11.D
D : x =1, y = 3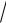 x, y = −x3.
x, y = −x3.
∫∫(12xy + 27x2 y2 )dxdy;
2.13.D
D: x =1, y = x2 , y = −3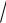 x.
x.
4 |
xy + |
9 |
|
x2 y2 |
|
||
|
|
|
|
|
dxdy; |
||
|
|
|
|
||||
2.15. ∫∫D 5 |
|
11 |
|
|
|||
D : x =1, y = x3, y = −
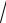 x.
x.
∫∫(24xy − 48x3 y3 )dxdy;
2.17.D
D: x =1, y = x2 , y = −
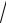 x.
x.
∫∫(4xy +16x3 y3 )dxdy;
2.19.D
D : x =1, y = 3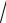 x, y = −x3.
x, y = −x3.
∫∫(44xy +16x3 y3 )dxdy;
2.21.D
D: x =1, y = x2 , y = −3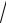 x.
x.
∫∫(xy − 4x3 y3 )dxdy;
2.23.D
D : x =1, y = x3, y = −
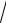 x.
x.
∫∫(27x2 y2 + 48x3 y3 )dxdy;
2.8.D
D : x =1, y = 
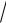 x, y = −x3.
x, y = −x3.
∫∫(12xy + 9x2 y2 )dxdy;
2.10.D
D: x =1, y = 
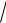 x, y = −x2.
x, y = −x2.
∫∫(24xy +18x2 y2 )dxdy;
2.12.D
D : x =1, y = x3, y = −3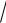 x.
x.
∫∫(8xy +18x2 y2 )dxdy;
2.14.D
D: x =1, y = 3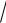 x, y = −x2.
x, y = −x2.
|
∫∫D |
4 |
xy + 9x2 y2 |
|
|
2.16. |
|
|
|||
|
5 |
||||
|
|
|
|
dxdy; |
|
D : x =1, y = 
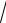 x, y = −x3.
x, y = −x3.
∫∫(6xy + 24x3 y3 )dxdy;
2.18.D
D: x =1, y = 
 x, y = −x2.
x, y = −x2.
∫∫(4xy +16x3 y3 )dxdy;
2.20.D
D : x =1, y = x3, y = −3 x.
x.
∫∫(4xy +176x3 y3 )dxdy;
2.22.D
D : x =1, y = 3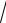 x, y = −x3.
x, y = −x3.
∫∫(4xy +176x3 y3 )dxdy;
2.24.D
D : x =1, y = 
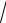 x, y = −x3.
x, y = −x3.
5

|
∫∫D |
|
6x2 y2 |
+ |
25 |
x4 y4 |
|
|||
2.25. |
|
|
|
|
||||||
3 |
|
|||||||||
|
|
|
|
|
dxdy; |
|||||
|
|
|
|
|
||||||
|
D : x =1, y = x2 , y = − x. |
|||||||||
|
∫∫D |
|
3x2 y2 |
+ |
50 |
|
x4 y4 |
|
||
2.27. |
|
|
|
|
||||||
3 |
|
|||||||||
|
|
|
|
|
dxdy; |
|||||
D: x =1, y = 3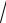 x, y = −x3.
x, y = −x3.
∫∫(54x2 y2 +150x4 y4 )dxdy;
2.29.D
D : x =1, y = x2 , y = −3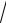 x.
x.
∫∫(54x2 y2 +150x4 y4 )dxdy;
2.31.D
D : x =1, y = x3, y = −
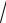 x.
x.
Задача 3. Вычислить.
∫∫yexy/2dxdy;
3.1.D
D : y = ln2, y = ln3, x = 2, x = 4.
∫∫ycos xy dxdy;
3.3.D
D : y = π /2, y = π , x =1, x = 2.
∫∫ysin xy dxdy;
3.5.D
D : y = π /2, y = π , x =1, x = 2.
∫∫4ye2xydxdy;
3.7.D
D : y = ln3, y = ln4, x = 1 , x =1. 2
∫∫(9x2 y2 + 25x4 y4 )dxdy;
2.26.D
D: x =1, y = 
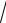 x, y = −x2.
x, y = −x2.
∫∫(9x2 y2 + 25x4 y4 )dxdy;
2.28.D
D : x =1, y = x3, y = −3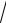 x.
x.
∫∫(xy − 9x5 y5 )dxdy;
2.30.D
D: x =1, y = 3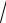 x, y = −x2.
x, y = −x2.
∫∫y2 sin |
xy |
dxdy; |
|
2 |
|||
3.2. D |
|
||
|
|
D : x = 0, y = 
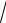 π , y = x. 2
π , y = x. 2
∫∫y2e−xy/4dxdy;
3.4.D
D : x = 0, y = 2, y = x.
xy
∫∫y2 cos 2 dxdy;
3.6. D
D : x = 0, y = 
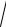 π
π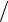 2, y = x
2, y = x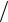 2.
2.
∫∫4y2 sin xy dxdy;
D |
|
|
|
3.8. |
|
|
|
π , y = x. |
|||
D: x = 0, y = |
|||
|
2 |
|
|
6
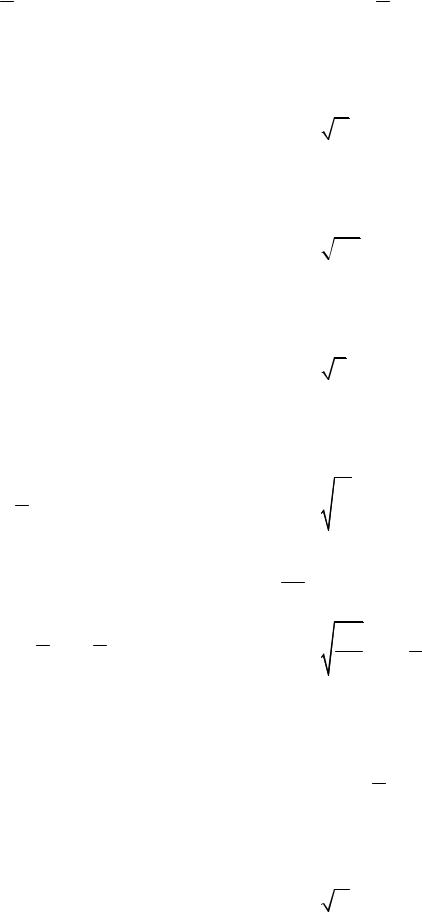
∫∫ycos2xy dxdy;
3.9. D
D : y = π , y = π , x = 1 , x =1.
22
∫∫12ysin2xy dxdy;
3.11. D
D : y = π , y = π , x = 2, x = 3.
42
∫∫yexy/4dxdy;
3.13.D
D : y = ln2, y = ln3, x = 4, x = 8.
∫∫2ycos2xy dxdy;
3.15. D
D : y = π , y = π , x =1, x = 2.
42
∫∫ysin xy dxdy;
3.17.D
D : y = π , y = 2π , x = 1 , x =1. 2
∫∫8ye4xydxdy;
3.19.D
D : y = ln3, y = ln4, x = 1 , x = 1. 4 2
∫∫ycos xy dxdy;
3.21.D
D : y = π , y = 3π , x =1 2, x =1.
2, x =1.
∫∫ysin2xy dxdy;
3.23.D
D : y = π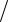 2, y = 3π
2, y = 3π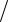 2, x =1
2, x =1 2, x = 2.
2, x = 2.
∫∫y2e−xy/8dxdy;
3.10.D
D : x = 0, y = 2, y = x. 2
∫∫y2 cos xy dxdy;
3.12.D
D: x = 0, y = 
 π , y = x.
π , y = x.
∫∫y2 sin2xy dxdy;
3.14.D
D : x = 0, y = 
 2π , y = 2x.
2π , y = 2x.
∫∫y2e− xy/2dxdy;
3.16.D
D: x = 0, y = 
 2, y = x.
2, y = x.
∫∫y2 cos2xy dxdy;
D |
|
|
|
|
|
3.18. |
|
|
|
|
|
π , y = |
x |
|
|||
D : x = 0, y = |
. |
||||
|
|||||
|
2 |
2 |
|
||
xy
∫∫3y2 sin 2 dxdy;
3.20. D
D : x = 0, y = 4π , y = 2 x. |
|
3 |
3 |
∫∫y2e−xy/2dxdy;
3.22.D
D : x = 0, y =1, y = x. 2
∫∫y2 cos xy dxdy;
3.24.D
D: x = 0, y = 
 π , y = 2x.
π , y = 2x.
7

∫∫6yexy/3dxdy;
3.25.D
D : y = ln2, y = ln3, x = 3, x = 6.
∫∫ycos2xy dxdy;
3.27.D
D : y = π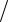 2, y = 3π
2, y = 3π 2, x =1
2, x =1 2, x = 2.
2, x = 2.
∫∫3ysin xy dxdy;
3.29.D
D: y = π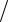 2, y = 3π , x =1, x = 3.
2, y = 3π , x =1, x = 3.
∫∫12ye6xydxdy;
3.31. D
D : y = ln3, y = ln4, x =1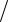 6, x =1
6, x =1 3.
3.
Задача 4. Вычислить.
∫∫∫2y2exy dx dy dz;
|
V |
|
4.1. |
x |
= 0, y =1, y = x, |
|
||
|
V |
= 0, z =1. |
|
z |
|
|
∫∫∫y2ch(2xy) dx dy dz; |
|
|
V |
|
4.3. |
x |
= 0, y = −2, y = 4x, |
|
||
|
V |
= 0, z = 2. |
|
z |
|
|
∫∫∫x2sh(3xy) dx dy dz; |
|
|
V |
|
4.5. |
x |
=1, y = 2x, y = 0, |
|
||
|
V |
= 0, z = 36. |
|
z |
|
|
∫∫y2 sin |
xy |
|
dxdy; |
||||
3.26. |
2 |
|||||||
D |
|
|
|
|
||||
|
|
|
|
|
||||
|
D: x = 0, y = π , y = x. |
|||||||
3.28. |
∫∫y2e−xy/8dxdy; |
|||||||
D |
|
|
|
|
|
|
||
|
D: x = 0, y = 4, y = 2x. |
|||||||
|
∫∫y2 cos |
xy |
dxdy; |
|||||
|
|
|||||||
3.30. |
D |
2 |
|
|
|
|
||
D : x = 0, y = 
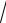 2π , y = 2x.
2π , y = 2x.
∫∫∫x2 zsin(xyz) dx dy dz;
|
V |
|
4.2. |
x |
= 2, y = π , z =1, |
|
||
|
V |
= 0, y =1, z = 0. |
|
x |
|
|
∫∫∫8y2 z e2xyz dx dy dz; |
|
|
V |
|
4.4. |
x |
= −1, y = 2, z =1, |
|
||
|
V |
= 0, y = 0, z = 0. |
|
x |
|
|
∫∫∫y2 zcos(xyz) dx dy dz; |
|
|
V |
|
4.6. |
x |
=1, y = 2π , z = 2, |
|
||
|
V |
= 0, y =1, z = 0. |
|
x |
|
8
|
|
|
|
π |
|
||
|
∫∫∫y2cos |
xy dx dy dz; |
|||||
|
|
V |
|
4 |
|
||
4.7. |
|
|
|
|
|
||
|
x |
= 0, y |
= −1, y = x 2, |
||||
|
|
||||||
|
V |
= 0, |
|
= −π 2. |
|||
|
|
z |
z |
||||
|
∫∫∫y2e−xy |
dx dy dz; |
|||||
|
|
V |
|
|
|
|
|
4.9. |
|
x |
= 0, y |
= −2, y = 4x, |
|||
|
|
||||||
|
V |
= 0, z |
=1. |
||||
|
|
z |
|||||
|
|
∫∫∫y2ch(2xy) dx dy dz; |
|||||
|
|
V |
|
|
|
|
|
4.11. |
x |
= 0, y =1, y = x, |
|||||
|
|
||||||
|
|
V |
|
= 0, z = 8. |
|||
|
|
z |
|||||
|
|
∫∫∫y2exy |
2 dx dy dz; |
||||
|
|
V |
|
|
|
|
|
4.13. |
x |
= 0, y = 2, y = 2x, |
|||||
|
|
||||||
|
|
V |
|
= 0, z = −1. |
|||
|
|
z |
|||||
|
|
|
|
|
π xy |
||
|
|
∫∫∫y2cos |
dx dy dz; |
||||
|
|
V |
|
|
|
2 |
|
4.15. |
|
|
|
|
|||
x |
= 0, y = −1, y = x, |
||||||
|
|
||||||
|
|
V |
|
= 0, z = 2π 2. |
|||
|
|
z |
|||||
∫∫∫y2cos(π xy) dx dy dz;
V
4.17.x = 0, y =1, y = 2x,
z = 0, z = π 2.V
∫∫∫x2sh(2xy) dx dy dz;
|
V |
4.19. |
x = −1, y = x, y = 0, |
|
|
|
V |
|
z = 0, z = 8. |
∫∫∫x2 zsin |
xyz |
dx dy dz; |
|||||
|
|
||||||
|
V |
4 |
|
|
|
||
4.8. |
|
|
|
|
|
|
|
|
x =1, y = 2π , z = 4, |
||||||
V |
|
|
|
|
|
|
|
|
x = 0, y = 0, z = 0. |
||||||
|
∫∫∫2y2 z e2xyz dx dy dz; |
||||||
|
V |
|
|
|
|
|
|
4.10. |
x |
=1, y =1, z =1, |
|||||
|
|||||||
|
V |
= 0, y = 0, z = 0. |
|||||
|
x |
||||||
|
∫∫∫x2 z sh(xyz) dx dy dz; |
||||||
|
V |
|
|
|
|
|
|
4.12. |
x |
= 2, y =1, z =1, |
|||||
|
|||||||
|
V |
= 0, y = 0, z = 0. |
|||||
|
x |
||||||
|
∫∫∫y2 zcos |
xyz |
|
dx dy dz; |
|||
|
|
||||||
|
V |
3 |
|
|
|||
4.14. |
|
|
|
|
|
|
|
|
x = 3, y =1, z = 2π , |
||||||
|
V |
= 0, y = 0, z = 0. |
|||||
|
x |
||||||
|
∫∫∫x2 z sh(xyz) dx dy dz; |
||||||
|
V |
|
|
|
|
|
|
4.16. |
x |
=1, y = −1, z =1, |
|||||
|
|||||||
|
V |
= 0, y = 0, z = 0. |
|||||
|
x |
||||||
|
∫∫∫2x2 z sh(2xyz) dx dy dz; |
||||||
|
V |
|
|
|
|
|
|
4.18. |
x |
= 2, y =1 2, z =1 2, |
|||||
|
|||||||
|
V |
= 0, y = 0, z = 0. |
|||||
|
x |
||||||
|
∫∫∫x2 z sin |
xyz |
dx dy dz; |
||||
|
|
||||||
|
V |
2 |
|
|
|||
4.20. |
|
|
|
|
|
|
|
|
x =1, y = 4, z = π , |
||||||
|
V |
= 0, y = 0, z = 0. |
|||||
|
x |
||||||
9
