Добавил:

Vezen Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Коломенский институт филиал МГМУ

Предмет:

Высшая математика

Файл:

Кузнецов_математика

.pdf

Скачиваний:

416

Добавлен:

20.06.2014

Размер:

3 Мб

Скачать

☆

<<< < Предыдущая 2 3 4 5 6 7 8 9 10 11 12 1314 / 2714 15 16 17 18 19 20 21 22 23 24 25 26 > Следующая >>>

∞ sin

2π

∞

3+ 7n

4.25. ∑

4.26. ∑

n=1

5n + n

∞

4.27. ∑n(e1 n −1)2 .

4.28. ∑nsin

n=1

3 n4

∞

4.29. ∑arctg

4.30. ∑sin

n=1

(n −1)5 n2 +1

n=1

n2 3 n + 5

∞

4.31. ∑arcsin

(n2 +

5 2

n=1

Задача 5. Исследовать на сходимость ряд.

∞

n +1

5.1. ∑

n=2

2n (n −1)!

5.3. ∑∞

2n+1 (n3 +1)

n=1

(n +1)!

∞

(2n + 2)!

5.5. ∑

3n +

n=1

∞

arctg

5.7. ∑

n=1

∞

5.9. ∑

n=1

(2n)! 5n

∞

5.11. ∑

(n +

2)!

n=1

∞

5.13. ∑

(2n −1)!

n=1

∞

1 3 5...(2n −1)

5.15. ∑

n=1

(n +1)!

∑∞ (n!)2

5.2. n=1 2n2 .

∑∞ 10n2n!

5.4. n=1 (2n)! .

∞	n + 5			2
5.6. ∑	n + 5		sin	2	.
5.6. ∑			sin		.
n=1	n!			3n
∞	n
5.8. ∑	n	.
5.8. ∑	n	.
n=1	3 n!

5.10. ∑∞		6n (n2 −1)			.

n=1			n!
∞		n	n
5.12. ∑				.
		(n!)2
n=1
∞		n!
5.14. ∑				.
	(3n!)
n=1

∑∞ n!

5.16. n=1 nn−1 . ?

∑∞ (n!)2

5.17. n=1 (3n +1)(2n)!.

∞

(n +1)!

5.19. ∑

n .

n=1

∞

5.21. ∑

n=1

∞

5.23. ∑

(n + 2)!4n

n=1

∞

1 4 7...(3n − 2)

5.25. ∑

7 9 11...(2n +

n=1

∞

(3n + 2)!

5.27. ∑

2 .

n=1

∞

5.29. ∑

n=1

3n + 2

∞

1 4 7...(3n − 2)

5.31. ∑

n=1

2n+1n!

5.18. ∑∞ n!sin π .

n=1 2n

∞

n 3

5.20. ∑

n=1

(n +1)!

∞

5n (n +1)!

5.22. ∑

n=1

(2n)!

∞

3 5 7...(2n +1)

5.24. ∑

2 5 8...(3n −1)

n=1

∞

2n!

5.26. ∑

n=1

2n + 3

4n−1

∞

n2 + 5

5.28. ∑

(

n −1 !

n=2

)

∞

n!(2n +1)!

5.30. ∑

(

n=1

3n)!

Задача 6. Исследовать на сходимость ряд.

∞

−n2

∞

1 n2

6.1. ∑

6.2. ∑

n=1

n +1

n=1

∞

2n2 +1 n2

∞

6.3. ∑

6.4. ∑n4

n=1

+ 5

∞

2n +1

∞

2n + 2 n

6.5. ∑

6.6. ∑

(n +1)

n=1

− 2

n=1

3n +1

∞

4n − 3

∞

6.7. ∑

6.8. ∑

n=1

10n

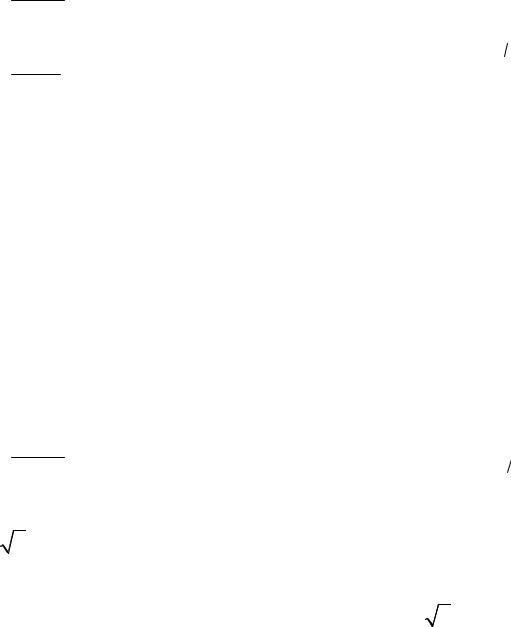
∞			π
6.9. ∑narcsinn						.

n=1			4n
∞	n −1	n		n
6.11. ∑							.
			5		n
n=1	n

6.13. ∑∞ 3n + 2 n (n −1)2 . n=1 4n −1

∑∞ n 2n+1

6.15. . n=1 3n +1

∞	n+1
6.17. ∑	2		.
	n
n=1	n
∞	n	3
6.19. ∑					.
	(lnn)			n
n=2

∞	π
6.21. ∑n3arctgn	π	.
6.21. ∑n3arctgn		.
n=1	3n
∞
6.23. ∑2n−1e−n .
n=1

∑∞ 2n n2

6.25. . n=1 4n + 3

∞			n						2n
			n
6.27. ∑ n								.
6.27. ∑ n					−			.
n=1			3n		−	1
∞			n+2
6.29. ∑	n 3			.
6.29. ∑	n			.
n=1		5
∞							π
6.31. ∑n4arctg2n							π			.
6.31. ∑n4arctg2n										.
n=1							4n

Задача 7. Исследовать на сходимость ряд.

∞

n + 2

6.10. ∑

3n −

n=1

∞

2n + 3 n2

6.12. ∑

n=1

n +1

∞

n +1

6.14. ∑

n=2

2n − 3

∞

2n −1

n 2

6.16. ∑

3n +

n=1

∞

6.18. ∑n2 sinn

n=1

∞

6.20. ∑

3n −

n=1

∞

6.22. ∑

(

2n +

n=1

∞

3n −1 2n

6.24. ∑n

n=1

+ 2

∞

n+2

6.26. ∑

(

)

n 2

n=1

2n2 +1

∞

n +1 n2

6.28. ∑

n=1

∞

n −

6.30. ∑3

n=2

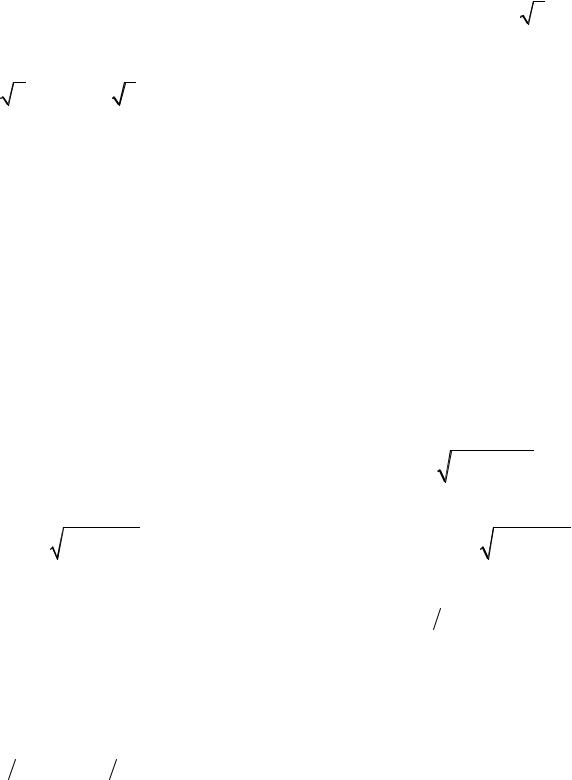
2n +1

∞

7.1. ∑

nln2 (3n +1)

n=2

∞

7.3. ∑

(2n +

3)ln2 (

2n +

n=1

∞

7.5. ∑

(3n +

4)ln2 (

5n +

n=1

∞

7.7. ∑

(n 2 +1)ln2 (n 3 +1)

n=1

∞

7.9. ∑

(2n −

1)ln(2n)

n=1

∞

7.11. ∑

(3n −1)lnn

n=2

∞

7.13. ∑

(2n − 3)ln(

3n +

n=2

∞

7.15. ∑

(n +

3)ln2 (

2n)

n=2

∞

7.17. ∑

nln(n −

n=3

∞

7.19. ∑

(n − 2)

ln(n − 3)

n=5

∞

7.21. ∑

(n +

5)ln2 (n +1)

n=2

∞

7.23. ∑n=2

(n3 +1)lnn

∞

7.25. ∑

(n 3−1)ln2 (n 2)

n=4

∞

7.2. ∑

nln2 (2n +1)

n=1

∞

7.4. ∑

(3n − 5)ln2 (4n −

n=3

∞

7.6. ∑

(2n +1)ln2 (n 5 + 2)

n=1

∞

7.8. ∑

(n − 2)ln(n − 3)

n=5

∞

7.10. ∑

(n +1)ln(2n)

n=1

∞

7.12. ∑

(2n −1)ln(n +1)

n=2

∞

7.14. ∑

(n + 2)ln2 n

n=2

∞

7.16. ∑

(2n + 3)ln2 (n +

n=2

∞

7.18. ∑

n=2 2n ln(

3n −1)

∞

7.20. ∑

(3n −1)

ln(n − 2)

n=4

∞

7.22. ∑

(n 3)ln2 (n + 7)

n=2

∞		n
7.24. ∑n=3
				.
	(n2	− 3)ln2 n
∞		n
7.26. ∑n=2
			.
	(n2	+ 5)lnn

∞	3n
7.27. ∑n=2
		.
	(2n2 + 3)lnn
∞	2n +1
7.29. ∑n=3
				.
	(3n2 2 + 2)ln(n 2)
∞	3n
7.31. ∑n=2
			.
	(n2 − 2)ln(2n)

Задача 8. Исследовать на сходимость ряд.

∞

n+1

2n +1

8.1. ∑(−1)

(

n=1

)

∞

(−1)

n+1

8.3. ∑

ln(n +

n=2

∞

(−1)n 2n2

8.5. ∑

n=1 n

− n

∞

(−1)

8.7. ∑

nln(n +1)

n=3

(−1)n sin

∞

8.9. ∑

3n +1

n=1

∑sinn

8.11..∞

n=1 n!

8.13. ∑∞ (−1)n tg 1 .

n=1 n

∞(−1)n−1

8.15.∑n=1 (n +1)22n .

∞	n +1
7.28. ∑n=4			.
	(5n2 − 9)ln(n − 2)
∞	n
7.30. ∑n=2
		.
	(n2 −1)lnn

∞		n+1			n			n
8.2. ∑(−1)		n+1			n
							.
							.
n=1				2n +1
∞	(−1)			n
∞
8.4. ∑						.
8.4. ∑						.
n=3	n(lnlnn)lnn
∞			n
∞	(−1)
8.6. ∑	(−1)				.
8.6. ∑					.
n=3	(n +1)lnn

∞(−1)n+1

8.8.∑n=1 n4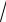2n + 3 .

∞

8.10. ∑(−1)n cos

n=1

∞

(−1)

8.12. ∑

nln(2n)

n=3

∞

cosn

8.14. ∑

n=1

(−1)

∞

8.16. ∑

n=1 cos

3 3n + lnn

∞

(−1)

n−1

8.17. ∑

(n +1)(3 2)

n=1

∞

(−1) (n + 3)

8.19. ∑

n=1

ln(n + 4)

(−1)n tg

∞

8.21. ∑

5n −1

n=1

sin(n

)

∞

8.23. ∑(−1)n

n=1

∞		π
8.25. ∑(−1)n sin				.

n=1		2n
∞		n
8.27. ∑(−1)n	sin3		.

n=1	3n

∞			1			1
8.29. ∑(−1)n sin			1	tg		1	.
8.29. ∑(−1)n sin				tg			.
n=1			n			n
∞		3
8.31. ∑(−1)n		n			.
8.31. ∑(−1)n	(	n +1 !			.
n=1	(			)

Задача 9. Вычислить сумму ряда с точностью

∞

2n −1

8.18. ∑(−1)n

n=1

∞

8.20. ∑(−1)n

n=1

∞

(−1)

8.22. ∑

(2n +1)22n+1

n=0

(−1)

∞

8.24. ∑

n=1 n + cos(2

n + 4)

∞

(−1)

8.26. ∑

n=1

n2 + sin2 n

∞

8.28. ∑(−1)

ln 1+

n=1

∞

8.30. ∑(−1)

− cos

n=1

α .

∞

n+1

(−1)

9.1. ∑(−1)n+1

, α = 0,01.

9.2. ∑

α = 0,01.

3n2

n=1

∞

9.3. ∑(−1)n+1

α = 0,001.

9.4. ∑(−1)n

, α = 0,001.

(2n)

n!(2n +1)

n=1

n=0

∞

2n +1

∞

(−1)

9.5. ∑(−1)n

, α = 0,01.

9.6. ∑

α = 0,0001.

n3 (n +1)

n=1

(2n +1)!

∞

(−1)

(−1) n

9.7. ∑

α = 0,1.

9.8. ∑

α = 0,1.

n=1

∞	(−1)n n					∞	(−1)n
9.9. ∑						, α = 0,001. 9.10. ∑			, α = 0,0001.
	(2n −1)	2	(2n	+1)	2		(2n +
n=1						n=1		1)!!

∞

(−1)n

9.11. ∑

α = 0,001.

(

n=1

2n)!!

∞

(−1)n n

9.13. ∑

α = 0,0001.

n=1

∞

(

−1)n

α = 0,001.

9.15. ∑

n=1

(2n)!

∞

(−1)n

9.17. ∑

α = 0,00001.

(

n=1

2n)!2n

∞

(−1)n

9.19. ∑

α = 0,001.

n=1

2n n!

∞

(−1)n

9.21. ∑

α = 0,00001.

(

n=1

2n)!n!

∞

(−1)n

9.23. ∑

α = 0,001.

4n (2n +1)

n=0

∞

(−1)n 2n

9.25. ∑

α = 0,001.

(n +1)

n=0

∞

sin(π 2 +π n)

9.27. ∑

, α = 0,01.

n3 +1

n=1

∞

cos(π n)

9.29. ∑

α = 0,001.

(

)

n=0

n3 +1

∞

(−1)n n

9.31. ∑

α = 0,001.

(

)

n=0

1+ n3

∞

9.12. ∑

−

α = 0,01.

n=0

∞

9.14. ∑

−

α = 0,1.

n=0

∞

(−1)n

α = 0,01.

9.16. ∑

3n!

n=0

∞

(−1)n (

2n +1)

9.18. ∑

, α

= 0,001.

(

n=1

2n)!n!

∞

(−1)n

α = 0,001.

9.20. ∑

n=1

3n n!

∞

cosπ n

9.22. ∑

, α = 0,001.

3n (n +1)

n=0

∞

sin(π 2 +π n)

9.24. ∑

, α

= 0,01.

n=1

∞

(−1)n

9.26. ∑

α = 0,001.

(n +1)

n=0

∞

(−1)n

9.28. ∑

, α = 0,01.

n3 (n + 3)

n=1

∞

(

−1)n

α = 0,01.

9.30. ∑

1+ n2

n=0

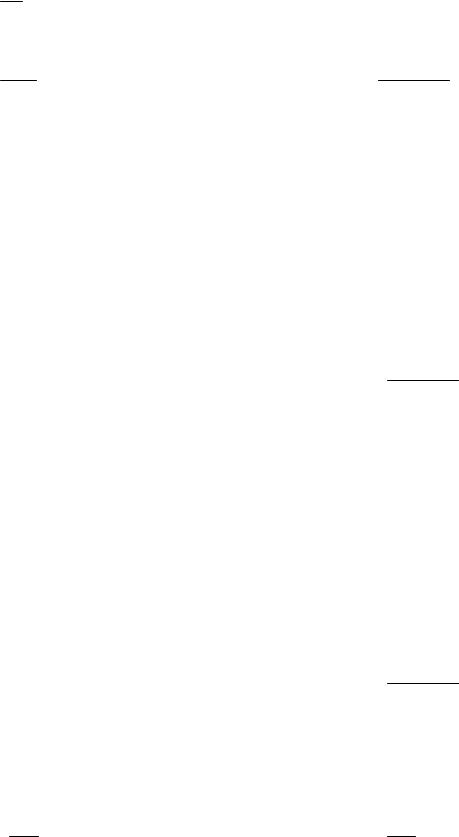
Задача 10. Доказать справедливость равенства. (Ответом служит число ρ , получаемое при применении признака Даламбера или признака Коши.)

10.1. lim n! = 0.

n→∞ nn

10.3. lim 2n!! = 0.

n→∞ nn

10.5. lim (2n)! = 0.

n→∞ 2n2 !

10.7. lim (2n)!! = 0.

n→∞ 5n2

10.9. lim (n +1)! = 0.

n→∞ nn

10.11. lim (2n −1)!! = 0.
n→∞	nn
10.13. lim (3n)!		= 0.
n→∞ 2n2
10.15. lim	n5	= 0.
	(2n)!
n→∞
10.17. lim (n + 2)! = 0.
n→∞	nn

10.19. lim (2n +1)!! = 0.

n→∞ nn

10.21. lim (4n)! = 0.

n→∞ 2n2

10.23. lim n3 = 0.

n→∞ 4n2

10.2. lim	nn	= 0.
	(2n)!
n→∞

10.4.lim (2n)n = 0. n→∞ (2n −1)!

10.6. lim		nn				= 0.

n→∞ (n!)2
10.8. lim	n2			= 0.

n→∞ n!
10.10. lim					nn		= 0.
		(	2n +1)!
n→∞

10.12.lim (3n)n = 0. n→∞ (2n −1)!

10.14. lim	nn			= 0.
10.14. lim	(n!)3			= 0.
n→∞	(n!)3
10.16. lim	23n		= 0.
10.16. lim			= 0.
n→∞ n!
10.18. lim		nn			= 0.
10.18. lim					= 0.
n→∞	(2n −1)!

10.20.lim (2n)n = 0. n→∞ (2n +1)!

10.22. lim	nn		= 0.


n→∞ (n +1)!		2

10.24. lim n! = 0.

n→∞ 2n2

10.25. lim (n + 3)! = 0.

n→∞ nn

10.27. lim (2n + 3)!! = 0.

n→∞ nn

10.29. lim (5n)! = 0.

n→∞ 2n2

10.31. lim n2 +1 = 0. n→∞ (2n)!!

10.26. lim	nn	= 0.
	(2n + 3)!
n→∞

10.28.lim (5n)n = 0. n→∞ (2n +1)!

10.30. lim = 0.

n→∞ (n + 2)! 2

Задача 11. Найти область сходимости функционального ряда.

∞

(−1)

11.1.

∑

−1 5

n=1

(x + n)

∞

11.3.

∑

+1(3x2 + 4x + 2)

n=1

∞

11.5.

∑

1− xn

n=1

∞

11.7.

∑

1+ x2n

n=1

∞

1+ x n

11.9.

∑

n=1

1− x

∞

11.11. ∑

2x+1

n=1

(

3 n2 + n +1)

∞

(

−1)

11.13. ∑

n=1

x + n

∞

(−1)n

1− x n

11.2.

∑

n=1

2n −

1+ x

∞

11.4.

∑

n +

(x2 − 4x + 6)n .

n=1

∞

11.6.

∑

n + 3

n=1

n +1 (27x2 +12x +

∞

11.8.

∑

n=1

n +1(3x2 + 8x +

11.10. ∑∞

(x2 − 6x +12)n .

n=1

4n (n2 +1)

∞

(−1)

11.12. ∑

(x + n)

n=1

11.14. ∑∞

(x2 − 5x +11)n .

n=1

5n (n2 + 5)

∞

(n + x) .

11.15. ∑

11.16. ∑

n(n + x)

n=1

∞

(−1)

∞

1+ x

11.17. ∑

11.18. ∑

(x + n)2

n=1

1− xn

∞

n +1

∞

11.19. ∑

11.20. ∑

xnx

−1

n=1

n=1 nx

∞

(25x2 +1)n .

∞

11.21. ∑n=1

11.22. ∑n=1

2n (n2 +1)

x2 + n2

∞

(−1)

11.23. ∑

11.24. ∑

n3 + 2 (3x2 +10x + 9)n

x + 2n

n=1

∞

n +

−n

11.25. ∑

11.26. ∑

(x + n)(x + n +1)

n=1

∞

(

−1 n

11.27. ∑n=1

11.28. ∑n=1

)

n(n + ex )

(n − ex )(n2 +1)

∞

(−1)

∞

11.29. ∑

11.30. ∑

(n − x)1 3

n=1

3nx +

∞

11.31. ∑

n + x2

n=1

Задача 12. Найти область сходимости функционального ряда.

	∞	9	n
12.1.	∑	9		x2n sin(x +π n).
12.1.	∑	n		x2n sin(x +π n).
	n=1	n
	∞	3	n
12.3.	∑	3		x4n cos(x +π n).
12.3.	∑	n		x4n cos(x +π n).
	n=1	n
	∞	2	3n
12.5.	∑	2			x4n sin(3x +π n).


	n=1	3 n

	∞	4	n
12.2.	∑	4		x4n sin(2x −π n).
12.2.	∑	n		x4n sin(2x −π n).
	n=1	n
	∞	5		n	1
12.4.	∑						x2n cos(x −π n).
12.4.	∑						x2n cos(x −π n).
	n=1		3			n
	∞	6	n
12.6.	∑	6		x2n sin(5x −π n).
12.6.	∑	n		x2n sin(5x −π n).
	n=1	n

<<< < Предыдущая 2 3 4 5 6 7 8 9 10 11 12 1314 / 2714 15 16 17 18 19 20 21 22 23 24 25 26 > Следующая >>>

Соседние файлы в предмете Высшая математика

#
20.06.2014381 Кб81Доказательства по линейной алгебре.docx
#
20.06.20143 Мб416Кузнецов_математика.pdf
#
20.06.2014952 Кб534Ответы на вопросы к экзамену по математике (шпаргалки).doc
#
20.06.20142 Мб189ТПУ Линейная алгебра 1курс ИДЗ №1.doc
#
20.06.2014380 Кб66ТПУ Линейная алгебра 1курс ИДЗ №2.doc
#
20.06.2014539 Кб61ТПУ Линейная алгебра 1курс ИДЗ №3.doc
#
20.06.20141 Мб67ТПУ Линейная алгебра 1курс ИДЗ №4.doc