
Кузнецов_математика
.pdf
9.5. y = arccos |
|
|
|
|
x2 − 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9.6. y = |
|
2 |
|
|
|
|
|
|
3x −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arctg |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x4 +16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
6x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
9.7. y = |
1 |
ln |
x −1 |
− |
1 |
|
|
|
arctg x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
4 |
|
|
x +1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
(x − 4) |
|
|
|
|
|
|
|
|
|
|
|
|
− 9arccos |
|
|
|
x −1 |
. |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9.8. y = |
8x − x2 − 7 |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
9.9. y = (1+ x)arctg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
2 + x2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
x |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
+ |
|
|
. |
|
|
|
|
|
9.10. y = |
|
arccos x − |
|
|
1− x2 . |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
3x |
|
|
|
x |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1+ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3+ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ 3arccos |
x |
. |
|||||||||||||||||||||||||
9.11. y = |
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9.12. y = |
|
x(2 − x) |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
arctg |
x. |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
x |
|
|
|
|
2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||||||||||||||||||||
|
|
4 |
+ x4 |
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
9.13. y = |
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
9.14. y = arcsin |
|
|
x |
|
+ arctg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
arctg |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x +1 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 + x |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
1 |
|
|
|
arccos x |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
9.15. y = |
|
−1 − |
. |
|
|
|
|
|
9.16. y = 6arcsin |
|
|
|
− |
|
x(4 − x) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
x − 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
−1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
9.17. y = |
|
|
|
6x − x2 − 8 + arcsin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9.18. y = (1+ x)arctg
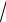 x −
x − 
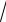 x . x
x . x
9.19. y = 2
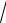 1− x arcsin
1− x arcsin 
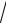 x + 2 .
x + 2 .
x x
x
9.20. y =
5x2 +1
9.21.y = arctg x + 6 ln 2 + 4.x
9.23. y = 1− x2 |
− xarcsin 1− x2 . |
|||||
|
|
|
|
|
|
|
9.25. y = arctg |
|
|
1− |
x |
|
. |
|
|
|
|
|
||
1 |
− x |
|||||
2x − 5 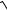
 5x
5x
4
9.22. y =
9.24. y =
9.26. y =
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− 4 − x2 + |
9 |
arcsin |
x −1 |
. |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
||||||||||||||||
4 |
|
3 |
|
|
|
|
|
|
|||||||||||||
arcsin |
|
x − 2 |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
(x −1) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
+ |
1 |
arctg |
|
|
+ |
8 |
arctg |
|
|
x |
. |
||||||||
|
x |
x |
|||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||
3 |
|
|
3 |
|
|
|
2 |
|
|
||||||||||||
(2x2 + 6x + 5)arctg x +1 − x. x + 2
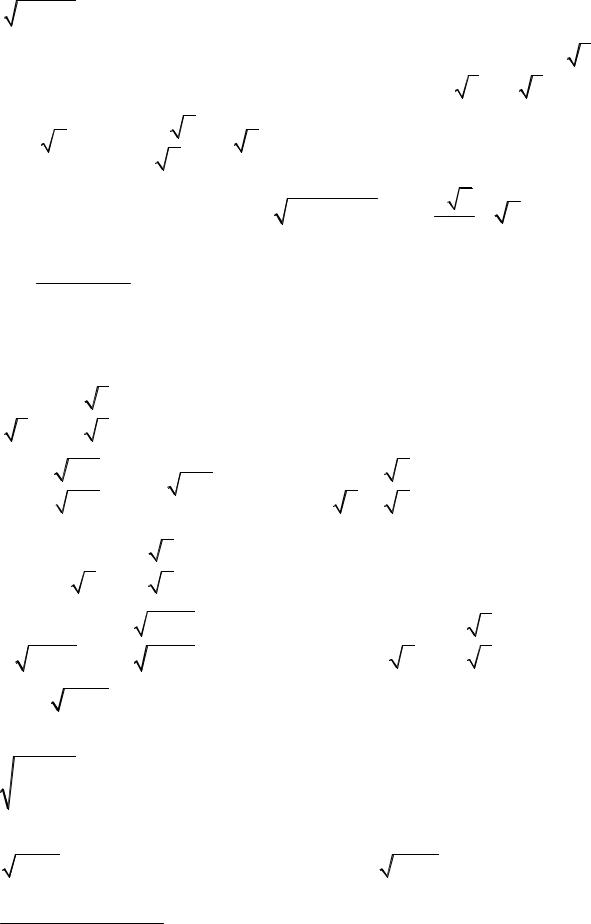
9.27. y = |
|
|
x |
|
arcsin2x + |
1 |
ln 1 |
− 4x2 |
) |
. |
|
|
|
|
|
||||||
2 |
1− 4x2 |
8 |
( |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
1 |
x2 −1 |
|
x3 |
|
|
3 |
|
|
||||||
|
|
|
|
|
|
|
9.28. |
y = |
2x |
|
− x + |
|
arctg |
|
|
|
|
− |
|
|
|
− |
|
|
|
x. |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
x 3 |
|
2 3 |
|
2 |
|
|
|||||||
9.29. y = (x + 2 |
|
+ 2)arctg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x |
|
|
x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
x + 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
9.30. y = 1+ 2x − x2 arcsin x
 2 − 2 ln(1+ x). 1+ x
2 − 2 ln(1+ x). 1+ x
9.31. y = arctg tg(x 2)+1. 2
2)+1. 2
Задача 10. Найти производную.
10.1. y = |
|
1 |
|
|
|
ln |
2 |
+ |
5 |
|
th x |
. |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
− |
|
|
|
||||||||||
4 |
5 |
2 |
5 th x |
|||||||||||||
|
|
|
1+ |
|
|
|
|
|
||||||||
|
1 |
|
th x |
|
|
|
|
|||||||||
10.3. y = |
ln |
|
− arctg th x. |
|||||||||||||
|
|
|
|
|||||||||||||
21−  th x
th x
10.5. y = |
1 |
th x + |
1 |
|
|
ln |
1+ |
|
2 |
|
th x |
. |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
2 |
|
|
|
|
|
|
4 2 |
|
|
|
1− |
|
2 th x |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
10.7. y = |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
a + |
1+ a2 th x |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln |
|
|
|
|
|
|
|
. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
2a 1+ a2 |
|
a − 1+ a2 th x |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
10.9. y = arctg |
|
|
|
|
sh2x |
. |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
ch x − sh x |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
10.11. y = 4 |
|
1+ th x |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
1− th x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
10.13. y = |
|
|
|
ch x |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
sh2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
10.15. y = 1+ 8ch2 x ln(ch x).
10.2. y = |
sh x |
|
|
+ |
|
3sh x |
|
|
+ |
3 |
arctg(sh x). |
|||||||||||||
4ch4 |
|
|
8ch2 x |
|
||||||||||||||||||||
|
x |
|
|
|
|
8 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
10.4. y = |
3 |
|
|
|
|
|
|
2 + th x |
− |
|
|
th x |
||||||||||||
|
|
|
ln |
|
|
|
|
|
|
|
|
. |
||||||||||||
8 |
|
|
|
|
|
|
|
|
|
|
4(2 − th2 x) |
|||||||||||||
2 |
|
|
2 − th x |
|||||||||||||||||||||
10.6. y = − |
1 |
|
|
|
|
x |
|
− |
|
ch x |
|
|
|
|||||||||||
|
|
ln th |
|
|
|
|
|
|
|
|
. |
|
||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
2sh |
|
x |
||||
10.8. y = |
|
1 |
|
|
|
ln |
1+ |
2 |
|
cth x |
. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
18 |
2 |
|
1− |
2 cth x |
||||||||||||||||
10.10. y = |
1 |
|
|
ln |
1− sh2x |
. |
||||||||||||||
|
|
|
|
|
|
|||||||||||||||
|
|
6 |
|
|
|
|
|
2 + sh2x |
||||||||||||
10.12. y = |
|
|
|
sh x |
. |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
1 |
+ ch x |
|
|
|
|
|
|
|||||||||||
10.14. y = |
|
|
|
sh3x |
|
. |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
ch6x |
|
|
|
|
|
|
||||||||
10.16. y = − |
12sh2 x +1 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|||||
|
|
|
3sh2 x |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||

10.17. y = − |
sh x |
+ |
3 |
arcsin(th x). |
10.18. y = |
1 |
|
arcsin |
3+ ch x |
. |
|
|
|
|
|
|
|
||||||
|
2ch2 x |
2 |
|
8 |
|
1+ 3ch x |
|||||
|
|
|
|
|
|
4 + |
|
|
|
|
th |
x |
|
|
|
|||
|
1 |
|
|
|
|
8 |
|
|||||||||||
10.19. y = |
|
ln |
2 |
. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
8 |
|
|
|
|
|
|
|
|
th |
|
x |
|
|
|
|||
|
|
|
|
4 − |
8 |
|||||||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
10.21. y = − |
1 |
arcsin |
5 |
+ 3ch x |
. |
|||||||||||||
|
|
|
|
|
||||||||||||||
|
4 |
|
|
|
3 |
+ 5ch x |
||||||||||||
10.23. y = |
2 |
|
|
− |
1 |
|
+ |
|
|
sh x |
||||||||
|
|
|
|
|
3sh3 |
|
|
2ch2 x |
||||||||||
|
sh x |
|
x |
|||||||||||||||
10.20. y = |
1 |
|
x |
|
|
− |
1 |
ln |
3+ ch x |
. |
||
ln |
th |
|
||||||||||
|
|
|
|
|||||||||
4 |
|
2 |
|
|
4 |
|
sh x |
|||||
10.22. y = 1− 8ch2 x. 4ch4 x
+5 arctg(sh x).
2
10.25. y = |
1 |
|
arctg(sh x)− |
sh x |
. |
|||||
|
|
|
|
|||||||
2 |
|
|
|
|
|
2ch2 x |
||||
10.27. y = − |
|
sh x |
− |
1 |
|
− |
3 |
arctg(sh x). |
||
|
2ch2 x |
|
|
|||||||
|
|
|
|
sh x |
2 |
|
|
|||
|
1 |
sh x |
|
|||
10.29. y = |
|
|
|
|
|
+ arctg(sh x) . |
|
|
2 |
|
|||
|
2 |
ch |
|
x |
|
|
2ch x
10.31.y = 3 cth x − 3sh3 x.
Задача 11. Найти производную.
11.1. y = (arctg x)(1 2)ln(arctg x) .
2)ln(arctg x) .
11.3. y = (sin x)5ex .
11.5. y = (ln x)3x .
11.7. y = (ctg3x)2ex .
11.9. y = (tg x)4ex .
10.24. y = |
8 |
cth2x − |
|
|
1 |
|
|
. |
|
|
|
|||
|
|
3ch x sh3 |
|
|
|
|
||||||||
|
3 |
|
|
|
|
x |
|
|
|
|||||
10.26. y = |
3 |
|
x |
|
+ ch x − |
|
ch x |
|
|
|||||
|
|
ln th |
|
|
|
|
|
|
|
|
. |
|||
|
|
|
|
|
|
|
2 |
|
||||||
|
2 |
|
2 |
|
|
|
2sh |
|
x |
|||||
10.28. y = |
|
sh x |
|
|
+ |
1 |
|
arctg(sh x). |
|||||
2ch2 x |
|
|
|||||||||||
|
2 |
|
|
|
|
|
|||||||
10.30. y = − |
|
ch x |
|
− |
|
1 |
|
x |
|||||
|
|
|
|
|
|
|
ln th |
|
. |
||||
|
|
2 |
|
|
|
|
|
||||||
|
|
|
2sh |
|
|
x 2 |
|
2 |
|||||
11.2. y = (sin 
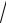 x )ln(sin
x )ln(sin  x) .
x) .
11.4. y = (arcsin x)ex .
11.6. y = xarcsin x.
11.8. y = xetg x .
11.10. y = (cos5x)ex .
11.11. y = (xsin x)8ln(xsin x) .
11.13. y = (x3 + 4)tg x .
11.15. y = (x2 −1)sh x .
11.17. y = (sin x)5x 2 .
2 .
11.19. y =19x19 x19.
11.21. y = (sin 
 x )e1
x )e1 x .
x .
11.23. y = xecos x .
11.25. y = xesin x .
11.27. y = xearctg x .
11.29. y = x29x 29x.
11.31. y = xex x9.
Задача 12. Найти производную.
11.12. y = (x − 5)ch x .
11.14. y = xsin x3 .
11.16. y = |
(x4 |
+ 5)ctg x . |
||
11.18. y = |
( |
x2 |
+1 |
cos x . |
|
|
) |
|
|
11.20. y = x3x |
2x. |
|
||
11.22. y = xectg x . |
|
|||
11.24. y = x2x |
5x. |
|
||
11.26. y = (tg x)ln(tg x) 4 .
4 .
11.28. y = (x8 +1)th x .
11.30. y = (cos2x)ln(cos2x) 4 .
4 .
12.1.y =
12.2.y =
1 |
( |
|
) |
|
|
|
|
+ |
x2 |
arcsin |
2 |
|
|||||
x2 + 8 |
x2 |
− 4 |
, x > 0. |
||||||||||||||
|
|
|
|||||||||||||||
24 |
|
|
|
|
|
16 |
|
|
|
|
x |
|
|||||
|
4x +1 |
|
|
+ |
1 |
|
arctg |
4x |
+ |
1 |
. |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
16x2 + 8x + 3 |
2 |
|
|
|
2 |
|
|
|
|||||||||
12.3.y = 2x − ln(1+ 
 1− e4x )− e−2x arcsin(e2x ).
1− e4x )− e−2x arcsin(e2x ).
12.4.y = 
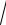 9x2 −12x + 5arctg(3x − 2)− ln(3x − 2 +
9x2 −12x + 5arctg(3x − 2)− ln(3x − 2 + 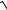
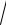 9x2 −12x + 5).
9x2 −12x + 5).
|
2 |
|
|
|
|
|
|
|
|
|
1+ 2x − x2 |
||||||||
12.5. y = |
|
2x − x |
2 + ln |
||||||||||||||||
|
|
|
|
|
|
|
|
. |
|
||||||||||
|
|
|
x −1 |
|
|||||||||||||||
|
x −1 |
|
|
|
|
|
|
|
|
|
|||||||||
|
x2 |
|
|
3 |
|
|
1 |
( |
|
) |
|
|
|
||||||
12.6. y = |
|
arcsin |
+ |
x2 +18 |
x2 |
− 9, x > 0. |
|||||||||||||
81 |
x |
81 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
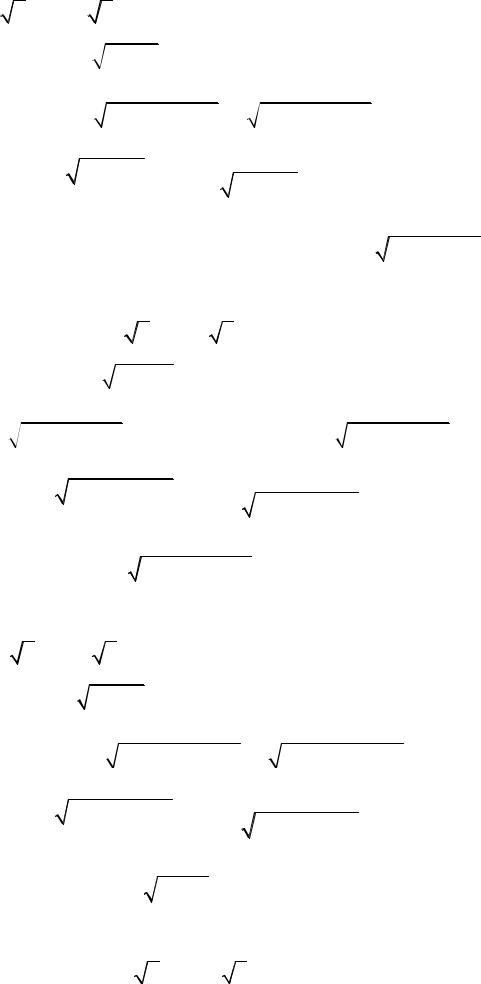
12.7. y = |
1 |
|
arctg |
3x |
− |
1 |
+ |
1 |
|
|
3x −1 |
. |
|
|
|
|
|
|
|
|
|
||||||
2 |
2 3 |
|
3x2 − 2x +1 |
||||||||||
12.8.y = 3x − ln(1+ 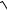
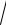 1− e6x )− e−3x arcsin(e3x ).
1− e6x )− e−3x arcsin(e3x ).
12.9.y = ln(4x −1+ 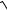
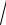 16x2 − 8x + 2)−
16x2 − 8x + 2)− 
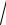 16x2 − 8x + 2 arctg(4x −1).
16x2 − 8x + 2 arctg(4x −1).
1+ 2 |
|
−x − x2 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
12.10. y = ln |
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
−x − x2 . |
|
|
|||||||
2x +1 |
|
|
|
|
2x +1 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|||
12.11. y = (2x + 3) |
4 |
arcsin |
|
|
|
+ |
|
(4x2 |
+12x +11) x2 |
+ 3x + 2, 2x + 3 > 0. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
2x + 3 |
3 |
|||||||||||||||||||||||
12.12. y = |
|
x + 2 |
|
|
+ |
1 |
|
|
|
arctg |
x + |
2 |
. |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
x2 |
+ 4x + 6 |
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||
12.13.y = 5x − ln(1+ 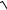
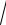 1− e10x )− e−5x arcsin(e5x ).
1− e10x )− e−5x arcsin(e5x ).
12.14.y = 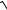
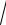 x2 − 8x +17 arctg(x − 4)− ln(x − 4 +
x2 − 8x +17 arctg(x − 4)− ln(x − 4 + 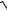
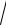 x2 − 8x +17).
x2 − 8x +17).
|
|
1+ −3+ 4x − x2 |
2 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
12.15. y = ln |
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
−3 |
+ 4x − x2 . |
|
|||||
|
|
2 − x |
|
|
|
− x |
|
||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|||||||||||||
12.16. y = (3x2 − 4x + 2) |
|
|
|
+ (3x − 2)4 arcsin |
1 |
|
|||||||||||||||||
9x2 −12x + 3 |
, 3x − 2 > 0. |
||||||||||||||||||||||
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x − 2 |
||
12.17. y = |
1 |
|
arctg |
x −1 |
+ |
|
x −1 |
. |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2 |
2 |
|
|
|
x2 − 2x + 3 |
|
|
|
|
|
|||||||||||||
12.18.y = ln(e5x + 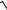
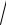 e10x −1)+ arcsin(e−5x ).
e10x −1)+ arcsin(e−5x ).
12.19.y = ln(2x − 3+ 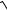
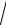 4x2 −12x +10)−
4x2 −12x +10)− 
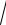 4x2 −12x +10arctg(2x − 3).
4x2 −12x +10arctg(2x − 3).
|
|
|
1+ −3− 4x − x2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
12.20. y = ln |
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
−3 |
− 4x − x2 . |
|
|
|||||||
−x − 2 |
|
|
|
|
|
x |
+ 2 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
2 |
(4x2 − 4x + 3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||||
12.21. y = |
|
|
|
x2 − x + (2x −1) |
4 |
arcsin |
, 2x −1 |
> 0. |
||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||
3 |
|
|
|
|
2x −1 |
|||||||||||||||||||||
12.22. y = |
|
|
2x −1 |
|
+ |
|
1 |
|
|
arctg |
2x |
− |
1 |
. |
|
|
|
|
|
|
|
|||||
4x2 − 4x + 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||

12.23.y = arcsin(e−4x )+ ln(e4x + 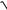
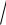 e8x −1).
e8x −1).
12.24.y = ln(5x + 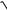
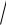 25x2 +1)−
25x2 +1)− 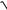
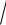 25x2 +1arctg5x.
25x2 +1arctg5x.
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
1+ −3+12x − 9x2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
12.25. y = |
|
|
|
|
|
|
−3+12x − |
9x2 + ln |
|
|
|
|
. |
||||||||||
3x − 2 |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x |
− 2 |
||||||||
12.26. y = (3x +1) |
4 |
|
|
|
|
|
|
1 |
|
+ (3x2 + 2x +1) |
|
|
|
|
|||||||||
arcsin |
|
|
|
9x2 + 6x, 3x +1> 0. |
|||||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
3x +1 |
||||||||||||||||||||||
12.27. y = |
1 |
|
arctg |
2x |
+ |
1 |
+ |
|
|
2x +1 |
. |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
2 |
|
|
|
|
2 |
|
|
|
|
4x2 + 4x + 3 |
|
|
|
|
||||||||
12.28.y = ln(e3x + 
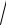 e6x −1)+ arcsin(e−3x ).
e6x −1)+ arcsin(e−3x ).
12.29.y = 
 49x2 +1arctg7x − ln(7x +
49x2 +1arctg7x − ln(7x + 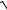
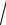 49x2 +1).
49x2 +1).
12.30.y = 1 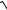
 1− 4x2 + ln1+
1− 4x2 + ln1+ 
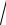 1+ 4x2 .
1+ 4x2 .
x 2x
12.31. y = arcsin(e−2x )+ ln(e2x + 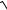
 e4x −1).
e4x −1).
Задача 13. Найти производную.
|
xarcsin x |
|
|
|
|
|
|
x |
|
|
1 |
− 4x2 |
|
||
13.1. y = |
+ ln 1 |
− x2 . |
13.2. y = 4ln |
|
− |
. |
|||||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
x2 |
||||||||
1− x2 |
|
|
|||||||||||||
|
|
|
|
|
1+ 1− 4x2 |
|
|
|
|
||||||
13.3.y = x(2x2 + 5)
 x2 +1 + 3ln(x +
x2 +1 + 3ln(x + 
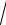 x2 +1).
x2 +1).
13.4.y = x3 arcsin x + x2 + 2 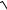
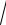 1− x2 .
1− x2 .
3
|
3 |
|
|
|
|
13.5. y = 3arcsin |
+ 2 4x2 + 2x − 2, 4x +1> 0. |
||||
|
|||||
|
4x +1 |
||||
13.6. y = 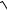
 1+ x2 arctg x − ln(x +
1+ x2 arctg x − ln(x + 
 1+ x2 ).
1+ x2 ).
|
2 |
|
|
|
|
13.7. y = 2arcsin |
+ 9x2 + 24x +12, 3x + 4 > 0. |
||||
|
|||||
|
3x + 4 |
||||
|
|
|
|
|
|
|
13.8. y = x(2x2 +1) |
|
|
|
− ln(x + |
|
|
|
). |
|||||||
|
|
|
|
|
|
|
x2 +1 |
x2 +1 |
||||||||||||||
13.9. y = ln(x + |
|
)− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1+ x2 |
. |
|
|
|
|
|
|
3 |
|
|
arcsin |
4x |
+ |
3 |
. |
||||||
x2 +1 |
13.10. y = 1− 3x − 2x2 + |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
x |
2 |
2 |
17 |
|
|
|
||||||||||||
13.11.y = 
 (4 + x)(1+ x) + 3ln(
(4 + x)(1+ x) + 3ln(
 4 + x +
4 + x + 
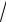 1+ x ).
1+ x ).
13.12.y = ln 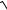
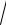 x2 − x +1 +
x2 − x +1 + 
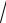 3arctg 2x −1.
3arctg 2x −1.
x |
3 |
13.13. y = |
1 |
ln |
x4 |
− x2 +1 |
− |
|
1 |
|
|
arctg |
|
|
3 |
|
. |
|||||
|
|
( |
|
|
|
) |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
−1 |
||||
|
12 |
|
|
|
|
|
2 |
|
2 |
3 |
|
2x |
||||||||
|
|
|
x |
2 |
+1 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
13.14. y = 4arcsin |
+ 4x2 +12x − 7, 2x + 3 > 0. |
||||
|
|||||
|
2x + 3 |
||||
|
2 |
|
|
|
|
13.15. y = 2arcsin |
+ 9x2 + 6x − 3, 3x +1> 0. |
||||
|
|||||
|
3x +1 |
||||
13.16. y = (2 + 3x)
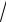 x −1 − 3 arctg
x −1 − 3 arctg
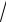 x −1. 2
x −1. 2
13.17. y = 1(x − 2)
 x +1 + ln(
x +1 + ln(
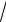 x +1 +1). 3
x +1 +1). 3
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
x2 +1 − x |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
13.18. y = |
x2 +1 − |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln |
|
|
|
. |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
x2 +1 +1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
13.19. y = ln 3 |
x −1 |
− |
1 |
|
1 |
+ |
|
1 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
arctg x. |
|
|
|
|
|
|
|
|
||||
x +1 |
|
|
|
2 |
−1 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
2 |
|
2 |
|
x |
|
|
|
|
|
|
|
|
|
|
||||
13.20. y = xln(
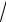 1− x +
1− x + 
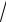 1+ x )+ 12(arcsin x − x).
1+ x )+ 12(arcsin x − x).
13.21. y = arctg |
|
− |
|
|
ln x |
|
. |
|
13.22. y = 3arcsin |
3 |
|
|
|
|
|
|||
x2 −1 |
|
+ x2 + 4x − 5. |
||||||||||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
x2 −1 |
|
|
|
x + 2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
13.23. y = |
|
|
|
|
+ 5arcsin |
x + 2 |
. |
|
|
|
|
|
||||||
(3− x)(2 + x) |
|
|
|
|
|
|||||||||||||
5 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13.24. y = x(arcsin x)2 + 2 |
|
|
||||||||
|
|
|
|
|
|
|
|
1− x2 arcsin x − 2x. |
||||||||||
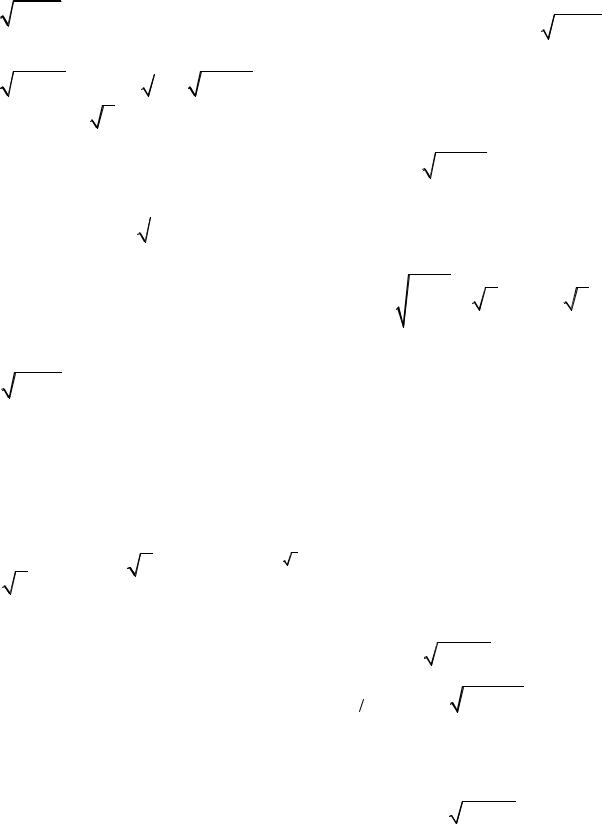
13.25. y =
13.27. y =
13.29. y =
13.31. y =
1− x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 + 2 |
|
|
|
|
|
|
|
||||||||
+ arcsin x. |
|
|
|
|
|
|
|
13.26. y = x2 arccos x − |
|
− x2 . |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|||||||||||||||||||||||||||
|
x |
3 |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x2 + 2 |
− |
1 |
|
|
|
|
|
|
2 + x2 + 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ln |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
( |
|
) |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13.28. y = |
x |
10 − x2 |
|
4 |
|
− x2 |
|
+ 6arcsin |
|
x |
. |
|||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
arcsin |
|
|
|
|
+ 2 |
|
|
x2 + 3x + 2, 2x + 3 > 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
2x + 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13.30. y = xarcsin |
|
− |
x + arctg |
|
|
x. |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x +1 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
arcsin x |
|
+ |
1 |
ln |
1− x |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
1− x2 |
|
2 1+ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Задача 14. Найти производную. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
14.1. y = |
|
1 |
|
|
|
ln |
(tg x + ctgα ). |
|
|
|
14.2. y = xcosα + sinα lnsin(x −α ). |
|||||||||||||||||||||||||||||||||||||
sinα |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1 |
|
|
|
|
sinln x − ( |
|
|
1) cosln x x |
|
+1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
14.3. y = |
|
|
|
|
|
|
2 − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos x |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14.4. y = arctg |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 cos2x |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
sin x |
|
|
|
|
sin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
2 |
+ b |
2 |
|
|
sin x |
|||||||||||||||||||||
14.5. y = 3 |
|
+ 2 |
. |
14.6. y = (a2 + b2 )−1 2 arcsin |
|
|
|
|
|
|
|
|
. |
|||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
cos |
x |
|
|
|
cos |
4 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
14.7. y = |
7x (3sin3x + cos3x ln7) |
. |
|
14.8. y = ln |
|
|
|
|
sin x |
|
|
|
|
|
|
|
. |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
9 + ln2 7 |
|
cos x + |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos2x |
|
|
|
|||||||||||||||||||||||||||
14.9. y = |
|
1 |
|
|
|
|
|
|
(acos x)+ alntg |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
arctg |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
a |
1+ a |
|
) |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14.10. y = − |
1 |
|
− |
1 |
|
|
+ |
1 |
ln |
1+ sin x |
. |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3sin3 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
sin x |
|
2 |
|
|
|
1− sin x |
||||||||||||||||
14.11. y = 1+ x2 |
|
) |
earctg x . |
|
|
|
|
|
|
|
14.12. y = |
ctg x + x |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1− xctg x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
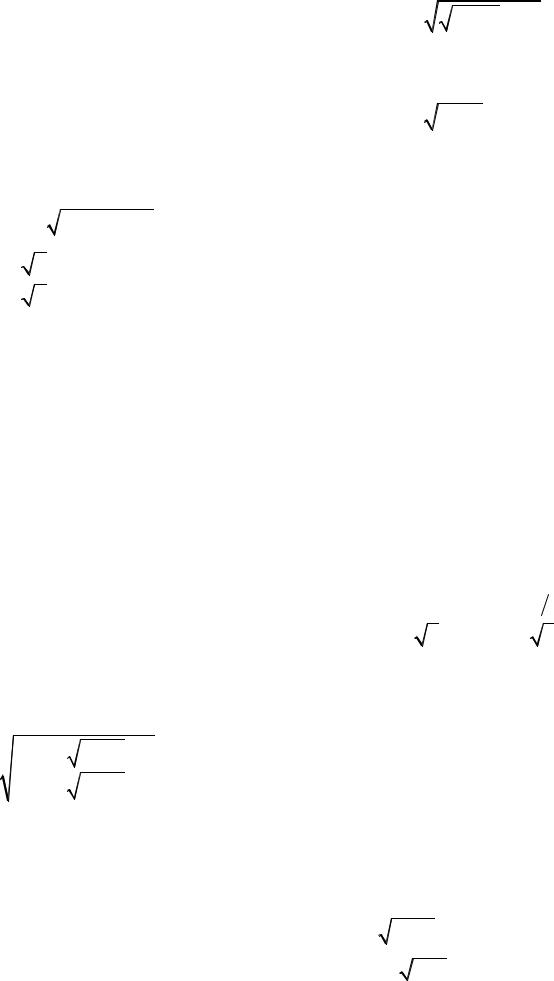
|
|
|
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
14.13. y = |
1 |
|
|
arctg |
2xsin 2 |
. |
|
14.14. y = arctg |
|
|
|
x4 +1 − x2 |
|
, x > 0. |
|||||||
|
α |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
2sin |
|
1− x2 |
|
|
|
|
|
x |
|
|
|
|||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
6x (sin4x ln6 − 4cos4x) |
|
|
|
|
|
|
|
|
|
|
||||||||||
14.15. y = |
14.16. y = arctg |
|
|
2tg x |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
. |
|
|
. |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
16 + ln2 6 |
1 |
− tg x |
|
|
|
||||||||||||
14.17. y = arctg |
|
2sin x |
|
. |
14.18. y = |
5x (2sin2x + cos2x ln5) |
. |
||||||||||||||
|
|
|
|
|
|||||||||||||||||
|
|
|
|
9cos2 x − 4 |
|
|
|
|
4 + ln2 5 |
|
|
|
|||||||||
14.19. y = ln |
|
|
2 |
+ th x |
. |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
2 − th x |
|
|
|
||
14.21. y = |
4x (ln4 sin4x − 4cos4x) |
||||||||
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
16 + ln |
2 4 |
|
|||
|
|
|
|
|
|
|
|||
14.23. y = |
5x (sin3x ln5− 3cos3x) |
||||||||
|
|
|
|
|
|
|
. |
||
|
|
|
|
9 + ln2 |
5 |
||||
|
|
|
|
|
|
|
|||
14.20. y = |
3x (4sin4x + ln3 cos4x) |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
16 + ln2 3 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
14.22. y = |
cos x |
− 2cos x − 3lntg |
x |
. |
|
|
|||||||
|
|
|
|
||||||||||
|
sin2 x |
|
|
|
2 |
|
|
|
|
||||
|
( |
|
) |
|
− |
x |
|
x |
|
||||
|
+ ex |
− 2e |
2 arctge |
2 . |
|||||||||
14.24. y = x − ln 1 |
|
|
|||||||||||
14.25. y = |
2x (sin x + cos x ln2) |
14.26. y = |
ln(ctg x + ctgα ) |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
1 |
+ ln2 2 |
|
|
|
|
|
|
|
|
|
|
sin |
|
|
|
|
|
|
|
||||||||||||||||||||
14.27. y = 2 |
|
cos x |
+ 3 |
cos x |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
sin4 x |
|
|
sin2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos x |
|
4 |
|
|
|
|
|
|
|
2tg |
(x 2) |
+1 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14.28. y = |
|
|
|
|
+ |
|
|
|
|
|
|
arctg |
|
|
|
|
|
|
|
|
. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3(2 + sin x) |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
3 |
|||||||||||||||||||||||||
14.29. y = |
3x (ln3 sin2x − 2cos2x) |
. 14.30. y = |
1 |
ln |
1+ cos x |
− |
|
1 |
− |
|
1 |
. |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
ln2 3+ 4 |
|
2 1− cos x |
|
|
|
|
|
cos x |
|
3cos3 |
x |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14.31. y = |
|
|
tg x + |
|
2tg x |
+1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
tg x − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
2tg x +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Задача 15. Найти производную y′x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
3t +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x = |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1− t |
2 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
3t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
15.1. |
|
|
|
|
t3 |
|
|
|
|
|
15.2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
y = tg 1+ t. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
y = sin |
|
|
+ t . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
x = |
|
|
|
|
|
|
|
|
|
|
|
||||
|
2t − t2 , |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
15.3. |
y = |
|
|
|
|
|
|
|
|
|
. |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3 |
|
(1− t) |
2 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
2 |
+1), |
||||
x = ln(t + t |
|
|
|
||||||||||||
15.5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
y = t |
|
|
t |
+1. |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||||
x = ctg(2et ),
y = ln(tget ).
x = arctget 2 ,
2 ,
15.9.
y = 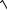 et +1.
et +1.
x = ln 1 ,
1− t4
y = arcsin1−t2 .
+ t21
|
|
|
|
|
|
|
|
|
|
|
|
), |
|
|
|
|
|
|
|
|
|
1−t |
2 |
|
|||||
x = arcsin( |
|
|
||||||||||||
15.13. |
(arccost)2 . |
|
|
|
|
|
||||||||
y = |
|
|
|
|
|
|||||||||
x = (1+ cos2 t)2 |
, |
|
|
|
|
|||||||||
15.15. |
cost |
|
|
|
|
|
|
|
|
|
|
|||
y = |
. |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||||
|
sin2 t |
|
|
|
|
|
|
|
||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|||
x = arccos |
|
|
, |
|
|
|
|
|
|
|||||
t |
|
|
|
|
|
|
||||||||
15.17. |
|
|
|
|
|
|
|
|
|
|
|
1 |
||
|
|
|
2 |
|
|
|
|
|
|
|
|
|||
y = |
|
t |
|
−1 + arcsin |
|
. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
x = arcsin(sint),
15.4.
y = arccos(cost).
x 2t t2 ,
y = arcsin(t −1).= −
x = ln(ctgt), |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15.8. |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
y = |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
cos |
|
t |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1− t |
|
|
|
|
|||||||||
x = ln |
|
, |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
15.10. |
|
|
|
|
|
|
|
|
|
1+ t |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1− t |
2 |
. |
|
|
|
|
|||||||||||||
y = |
|
|
|
|
|
|
|
|||||||||||||||
x = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1− t2 , |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|||
15.12. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
y = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1− t2 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|||
x = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1− t |
2 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
15.14. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ |
|
|
|
|
|
1−t2 |
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
y = ln |
|
|
|
|
|
|
|
|
. |
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|||||
|
|
|
|
|
|
1− t |
|
|
|
|
|
|
|
|
|
|||||||
x = ln |
|
|
|
|
|
|
, |
|
|
|
|
|||||||||||
|
+ t |
|
|
|
|
|||||||||||||||||
15.16. |
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1− t |
2 |
. |
|
|
|
|
|||||||||||||
y = |
|
|
|
|
|
|
|
|||||||||||||||
x = 1 ,
lnt
y = ln1+  1−t2 .t
1−t2 .t
