
Кузнецов_математика
.pdf
|
|
3 |
|
1 |
|
|
|
|
|
|
|
arctg x3 − x |
2 |
sin |
|
, |
|
|
|||||
1.9. f (x) = |
|
|
|
3x |
|
|
x = 0. |
|
|
|
|
0, |
|
|
|
|
|
|
|
2 |
|
6 |
|
|
x + arcsin x |
|
sin |
|
|
, |
|
|
|
|||||
1.11. f (x) = |
|
|
|
x |
|
|
=0, x 0.
x ≠ 0;
|
5 |
|
|
|
1.10. f (x) = sin x cos |
|
, |
x ≠ 0; |
|
x |
||||
|
x = 0. |
|
|
|
0, |
|
|
||
x ≠ 0;
|
|
( |
) |
|
1.12. f (x) = tg(2 |
x |
2 cos 1 8x |
|
−1+ x), x ≠ 0; |
|
|
|
||
|
|
= 0. |
|
|
0, x |
|
|
||
|
|
|
|
|
|
|
|
|
|
7 |
|
|
||
arctgx sin |
|
|
, |
x ≠ 0; |
||||||||||
|
||||||||||||||
1.13. f (x) = |
|
|
|
|
|
|
|
|
|
|
x |
|
||
|
|
|
x = 0. |
|
|
|
|
|||||||
0, |
|
|
|
|
|
|||||||||
|
2 |
|
|
|
|
2 11 |
|
|
x ≠ 0; |
|||||
x |
|
cos |
|
|
|
, |
|
|
||||||
|
|
|
|
|
||||||||||
1.15. f (x) = |
|
|
|
|
|
|
|
x |
|
|
|
|
||
|
|
|
x = 0. |
|
|
|
|
|||||||
0, |
|
|
|
|
|
|||||||||
|
lncos x |
, |
x ≠ 0; |
|||||||||||
|
|
|
||||||||||||
1.17. f (x) = |
|
|
x |
|
|
|
|
|
|
|
|
|||
|
|
|
x = 0. |
|
|
|
|
|||||||
0, |
|
|
|
|
|
|||||||||
ex2 |
− cos x |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
, x ≠ 0; |
||
|
|
|
|
|
|
|
|
|
|
|
||||
1.19. f (x) = |
|
|
|
x |
|
|
|
|
|
|
|
|
||
|
|
|
x = 0. |
|
|
|
|
|||||||
0, |
|
|
|
|
|
|||||||||
x2 sin |
2 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||||
1.21. f (x) = 3 |
|
|
|
x |
−1+ 2x, |
x ≠ 0; |
||||||||
0, |
|
x = 0. |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
+ x |
2 |
|
|
|
1 |
|
x ≠ 0; |
||
2x |
|
|
cos |
|
|
, |
|||||
|
|
|
|
||||||||
1.14. f (x) = |
|
|
|
|
|
|
|
9x |
|
||
|
|
x = 0. |
|
|
|
|
|
|
|||
0, |
|
|
|
|
|
|
|
||||
|
2 |
+ x |
2 |
|
|
|
1 |
|
|
x ≠ 0; |
|
2x |
|
|
cos |
|
, |
|
|||||
|
|
|
|
||||||||
1.16. f (x) = |
|
|
|
|
|
|
|
x |
|
||
|
|
x = 0. |
|
|
|
|
|
|
|||
0, |
|
|
|
|
|
|
|
||||
|
+ xsin |
1 |
|
|
x ≠ 0; |
||||||
6x |
|
, |
|
||||||||
|
|
||||||||||
1.18. f (x) = |
|
|
|
|
|
x |
|
|
|
|
|
|
|
x = 0. |
|
|
|
|
|
|
|||
0, |
|
|
|
|
|
|
|
||||
xsin |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1.20. f (x) = e |
|
x −1, |
x ≠ 0; |
|
|||||||
0, |
|
x = 0. |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ 3x |
2 |
|
2 |
−1, |
x ≠ 0; |
||
1+ln |
|
|||||||||
1 |
|
cos |
|
|
||||||
|
|
|||||||||
1.22. f (x) = |
|
|
|
|
|
x |
|
|
||
|
x = 0. |
|
|
|
|
|
|
|||
0, |
|
|
|
|
|
|
||||

xsin |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
2tgx − 2sin x |
|
|
|
x ≠ 0; |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
1.23. f (x) = e |
|
5x −1, |
x ≠ 0; |
|
|
1.24. f (x) = |
|
|
|
|
|
, |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
0, |
|
x = 0. |
|
|
|
|
|
|
|
|
|
|
x = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
3x |
− x |
2 |
|
|
1 |
|
x ≠ 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
arctg |
|
|
|
|
|
sin |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
1.25. f (x) = |
|
2 |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
x = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
x |
|
|
sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.26. f (x) = e |
|
|
|
|
|
|
−1+ x2 , |
x ≠ 0; |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
= 0. |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1.27. f (x) = 3 1 |
− 2x3 sin |
|
|
|
|
−1+ x, |
x ≠ 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
x = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
x |
|
|
1 |
|
|
x ≠ 0; |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.28. f (x) = |
x |
|
e |
|
|
sin |
x2 |
, |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = 0. |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
|
|
|
|
|
||||||||
|
ln(1+ 2x2 + x3 ) |
, x ≠ 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
1.29. f (x) = |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
x = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos x − cos3x |
, |
x ≠ 0; |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.30. f (x) = |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = 0. |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1− cos xsin |
|
|
|
, |
x ≠ 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
1.31. f (x) = |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
x = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Задача 2. Составить уравнение нормали (в вариантах 2.1 – 2.12) или уравнение
касательной (в вариантах 2.13 – 2.31) к данной кривой в точке с абсциссой x0 .
2.1. |
y = (4x − x2 ) |
4, x0 = 2. |
2.2. y = 2x2 + 3x −1, x0 |
= −2. |
||
|
y = x − x3, x |
= −1. |
|
|
|
|
2.3. |
2.4. y = x2 + 8 x −32, |
x = 4. |
||||
|
0 |
|
|
|
|
0 |

2.5. y = x + |
|
|
|
|
x3 , |
x |
|
|
=1. |
|
|
|
|
|
|
2.6. y = 3 x2 |
− 20, |
x |
|
= −8. |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2.7. y = |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
= 4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
, |
|
|
x |
|
|
|
|
|
|
|
2.8. y = 84 x − 70, |
x |
=16. |
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
1− |
|
|
|
x |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
2.9. y = 2x2 − 3x +1, |
|
x0 |
=1. |
|
|
|
|
|
2.10. y = (x2 − 3x + 6) |
|
|
|
x2 , |
|
|
x0 = 3. |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.12. y = (x3 + 2) |
(x3 − 2), |
|
= 2. |
||||||||||||||||||||||||||||
2.11. y = |
|
|
x − 33 |
x, |
|
|
|
x0 |
= 64. |
|
|
|
|
x0 |
|||||||||||||||||||||||||||||||||||||||||||
2.13. y = 2x |
2 + 3, |
|
x |
|
= −1. |
|
|
|
|
|
2.14. y = |
x29 |
+ 6 |
|
, |
|
x |
|
|
|
|
=1. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
x4 +1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2.15. y = 2x + |
1 |
|
, |
x0 |
=1. |
|
|
|
|
|
|
2.16. y = −2(x8 + 2) (3(x4 +1)), |
x0 |
=1. |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2.17. y = |
x5 +1 |
, |
|
x |
=1. |
|
|
|
|
|
|
|
2.18. y = |
x16 + 9 |
, |
|
x |
|
|
|
|
=1. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
x4 +1 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
1− 5x2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
2.19. y = 3(3 |
|
|
− 2 |
|
|
), |
x0 =1. |
2.20. y =1 (3x + 2), |
|
|
|
|
x0 |
= 2. |
|
|
|
||||||||||||||||||||||||||||||||||||||||
x |
x |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
2.21. y = x (x2 +1), |
|
|
|
x0 = −2. |
2.22. y = (x2 − 3x + 3) |
3, |
x0 |
= 3. |
|||||||||||||||||||||||||||||||||||||||||||||||||
2.23. y = 2x |
|
(x2 +1), |
|
x0 =1. |
2.24. y = −2(3 |
|
+ 3 |
|
|
|
|
|
), |
|
|
|
=1. |
||||||||||||||||||||||||||||||||||||||||
|
|
x |
x |
x0 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
2.25. y = |
1+ 3x2 |
|
|
|
|
|
|
=1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
, |
|
x |
|
|
|
|
|
|
2.26. y =14 |
|
x −153 |
|
x + 2, |
|
|
x |
=1. |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
3+ x2 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.28. y = (3x − 2x3 ) |
|
|
|
|
|
=1. |
|
|
|||||||||||||||||||||||||||||
2.27. y = 34 |
x − |
|
x, |
|
|
|
x0 |
=1. |
|
|
|
|
|
3, |
|
|
x0 |
|
|
||||||||||||||||||||||||||||||||||||||
2.29. y = x2 |
10 + 3, |
|
|
|
x0 = 2. |
|
|
|
|
|
2.30. y = (x2 − 2x − 3) |
4, |
|
x0 |
= 4. |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
2.31. y = 63 |
|
x −164 |
x |
3, |
|
x |
=1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 3. Найти дифференциал dy. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
3.1. y = xarcsin(1 x)+ ln |
x + |
|
x2 −1 |
, |
x > 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.2. y = tg(2arccos |
|
|
|
|
|
), |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1− 2x2 |
x > 0. |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
3.3. y = |
1+ 2x − ln |
x + |
|
1+ 2x |
. |
3.4. y = x2 arctg |
x2 −1 − |
|
x2 −1. |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
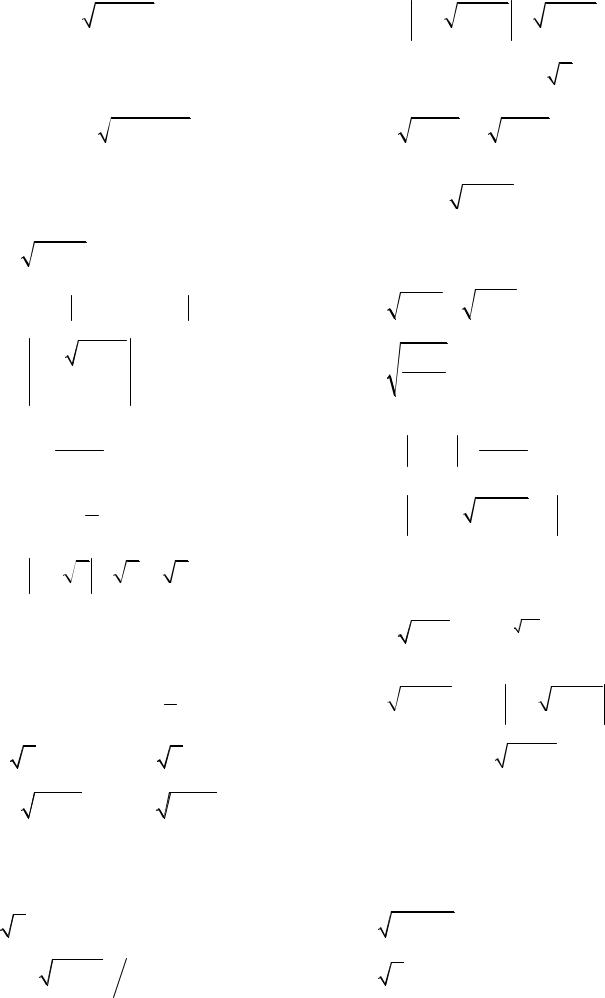
3.5. y = arccos(1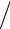
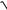
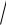 1+ 2x2 ), x > 0.
1+ 2x2 ), x > 0.
3.7. y = arctg(sh x) + (sh x)lnch x.
3.9. y = ln(cos2 x + 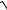
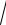 1+ cos4 x).
1+ cos4 x).
3.11. y = |
|
ln |
x |
|
|
− |
1 |
ln |
|
x2 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
+ x |
2 |
|
|
+ x2 |
|||||
|
1 |
|
2 |
1 |
|||||||
3.13. y = x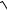
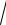 4 − x2 + aarcsin(x
4 − x2 + aarcsin(x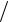 2).
2).
3.15. y = 2x + ln sin x + 2cos x .
3.17. y = ln |
x + |
x2 +1 |
|
|
|
. |
|
|
|
||
2x
3.19.y = arctg x2 −1. x
3.21. y = arctg tg x +1 .
2
3.23. y = ln cos
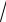 x +
x + 
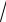 x tg
x tg
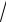 x.
x.
3.25. y = x(sinln x − cosln x).
3.27. y = cos x lntg x − lntg x. 2
|
y = |
|
|
− (1+ x)arctg |
|
|
|
|
|||
3.29. |
x |
x. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3.31. |
y = x |
|
|
x2 −1 + ln |
x + |
x2 −1 |
. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
3.6. y = xln x + 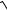
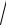 x2 + 3 −
x2 + 3 − 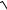
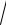 x2 + 3.
x2 + 3.
3.8.y = arccos((x2 −1)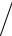 (x2
(x2 
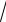 2)).
2)).
3.10.y = ln(x + 
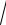 1+ x2 )−
1+ x2 )− 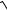
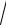 1+ x2 arctg x.
1+ x2 arctg x.
3.12.y = ln(ex + 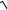
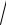 e2x −1)+ arcsinex .
e2x −1)+ arcsinex .
3.14. y = lntg(x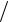 2)− x
2)− x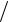 sin x.
sin x.
3.16. y = 
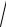 ctg x −
ctg x − 
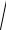 tg3 x
tg3 x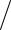 3.
3.
 x + 2
x + 2
3.18. y = 3 x − 2.
3.20. y = ln x2 −1 − 1 . x2 −1
3.22. y = ln 2x + 2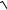
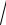 x2 + x +1.
x2 + x +1.
3.24. y = ex (cos2x + 2sin2x).
|
|
|
1 |
|
|
|
|
|
|
2 |
x−1 |
|
|||
3.26. y = |
x −1 − |
|
e |
|
|
. |
|
|
|
|
|||||
|
|
|
2 |
|
|
|
|
3.28. y = 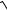
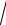 3+ x2 − xln x +
3+ x2 − xln x + 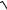
 3+ x2 .
3+ x2 .
3.30. y = xarctg x − ln 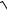
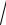 1+ x2 .
1+ x2 .
Задача 4. Вычислить приближенно с помощью дифференциала.
|
|
|
|
|
|
|
|
|
|
|
4.1. |
y = 3 x, |
x = 7,76. |
4.2. |
y = 3 |
x3 + 7x, x =1,012. |
|||||
|
y = (x + |
|
|
) 2, x = 0,98. |
|
|
|
|
||
|
|
|
|
|
|
|
||||
4.3. |
|
5 − x2 |
4.4. |
y = 3 |
x, x = 27,54. |
|||||
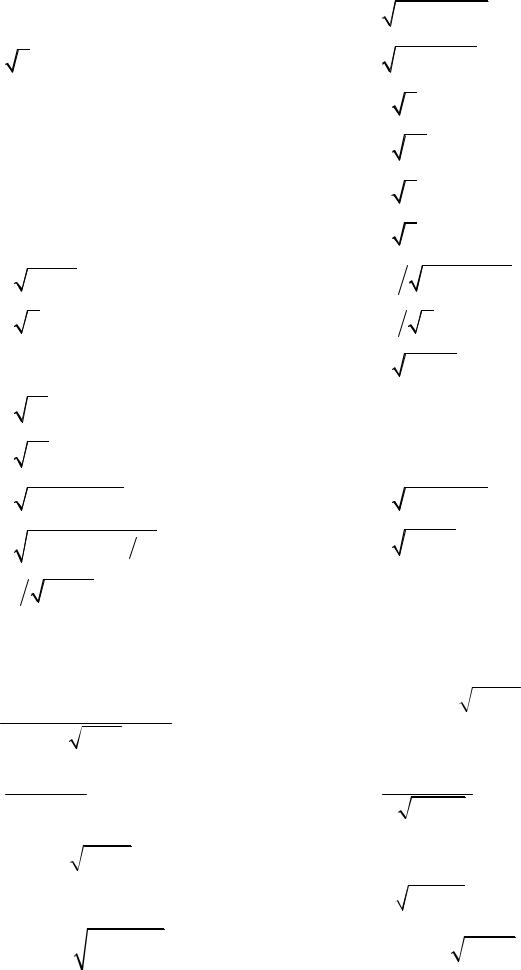
4.5. y = arcsin x, x = 0,08.
|
|
|
|
|
|
|
|
4.7. y = 3 x, |
x = 26,46. |
||||||
4.9. y = x11, x =1,021. |
|||||||
4.11. y = x21, |
x = 0,998. |
||||||
4.13. y = x6 , |
x = 2,01. |
||||||
4.15. y = x7 , |
x =1,996. |
||||||
|
|
|
|
|
|
||
4.17. y = |
4x −1, x = 2,56. |
||||||
4.19. y = 3 |
|
|
|
x = 8,36. |
|||
x, |
|||||||
4.21. y = x7 , |
x = 2,002. |
||||||
4.23. y = |
|
|
x = 0,98. |
||||
x3 , |
|||||||
4.25. y = 5 |
|
|
x =1,03. |
||||
x2 , |
|||||||
|
|
|
|||||
4.27. y = |
1+ x + sin x, x = 0,01. |
||||||
|
y = 4 |
|
|
|
, x =1,02. |
4.29. |
2x − sin(π x 2) |
||||
|
|
|
|
||
4.31. |
y =1 2x +1, x =1,58. |
||||
Задача 5. Найти производную.
5.1. y = 2(3x3 + 4x2 − x − 2). 15
 1+ x
1+ x
x4 − 8x2
5.3. y = 2(x2 − 4).
5.5. y = (1+ x8 )
 1+ x8 .
1+ x8 .
5.7. y = (x2 − 6)
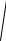 (4 + x2 )3 . 120x5
(4 + x2 )3 . 120x5
4.6. y = 3 |
x2 + 2x + 5, |
|
x = 0,97. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||
4.8. y = |
x2 + x + 3, |
x =1,97. |
||||||||||
4.10. y = 3 |
|
|
|
|
x =1,21. |
|||||||
x, |
||||||||||||
4.12. y = 3 |
|
|
|
x =1,03. |
||||||||
x2 , |
||||||||||||
4.14. y = 3 |
|
|
|
x = 8,24. |
||||||||
x, |
||||||||||||
4.16. y = 3 |
|
|
|
x = 7,64. |
||||||||
x, |
||||||||||||
|
|
|
|
|
|
|
|
|||||
4.18. y =1 |
|
|
2x2 + x +1, x =1,016. |
|||||||||
|
|
|
|
|
|
|
|
|||||
4.20. y =1 |
|
|
x , x = 4,16. |
|||||||||
|
|
|
|
|
|
|
||||||
4.22. y = |
|
4x − 3, |
x =1,78. |
|||||||||
4.24. y = x5, |
x = 2,997. |
|||||||||||
4.26. y = x4 , |
x = 3,998. |
|||||||||||
|
|
|
|
|
|
|||||||
4.28. y = 3 3x + cos x, |
|
x = 0,01. |
||||||||||
|
|
|
|
|
||||||||
4.30. y = |
|
x2 + 5, |
x =1,97. |
|||||||||
5.2. y = (2x2 −1)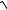
 1+ x2 . 3x3
1+ x2 . 3x3
5.4. y = 2x2 − x −1. 3
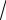 2 + 4x
2 + 4x
x2
5.6.y =  . 2
. 2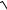 1− 3x4
1− 3x4
5.8. y = (x2 − 8)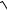
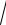 x2 − 8 . 6x3
x2 − 8 . 6x3
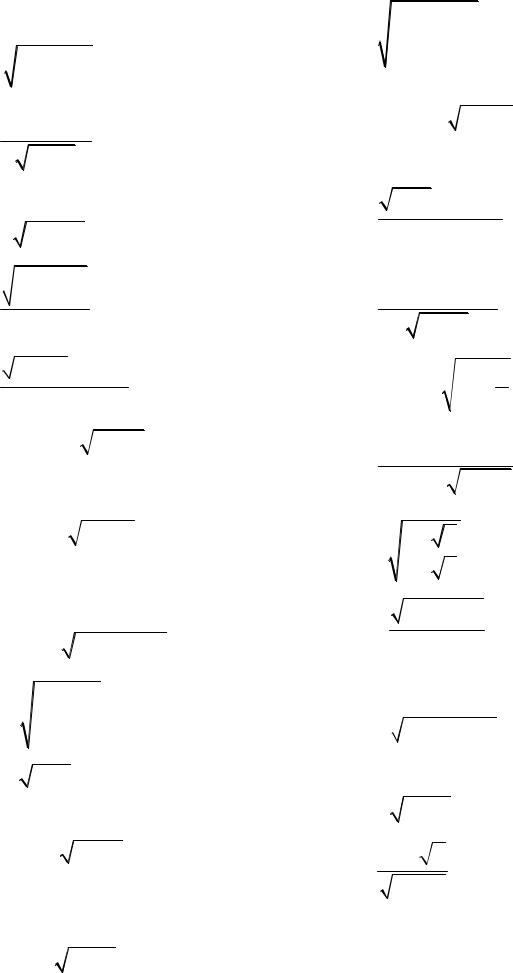
5.9. y = |
|
4 |
+ 3x3 |
|||
|
|
|
|
|
. |
|
|
|
|
|
|
||
|
x3 |
( |
2 + x3 )2 |
|||
5.11. y = x6 + x3 − 2.
|
|
|
1− x3 |
||
5.13. y = |
|
1+ x2 |
|||
|
|
|
|
. |
|
|
|
|
|
||
|
|||||
2 |
1+ 2x2 |
||||
5.15. y = 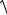
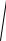 (1+ x2 )3 . 3x3
(1+ x2 )3 . 3x3
5.17.y = 
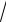 2x + 3(x − 2). x2
2x + 3(x − 2). x2
5.19. y = (2x2 + 3)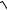
 x2 − 3 . 9x3
x2 − 3 . 9x3
5.21.y = (2x +1)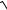
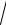 x2 − x . x2
x2 − x . x2
5.23. y = |
1 |
|
. |
|
|
|
|
||
(x + 2) |
|
|
||
x2 + 4x + 5 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
5.25. y = 3 3 |
|
(x +1) |
. |
|
|
|
||||||
|
|
|
|
|
|
|||||||
|
|
|
(x −1)2 |
|||||||||
|
|
|
|
|
|
|
|
|
||||
5.27. y = |
x |
x +1 |
. |
|
|
|
||||||
|
|
|
|
|||||||||
|
x2 + x +1 |
|||||||||||
5.29. y = (x + 3) |
|
|
. |
|
||||||||
2x −1 |
||||||||||||
|
|
|
2x + 7 |
|||||||||
5.31. y = |
3x6 |
+ 4x4 − x2 − 2 |
||||||||||
|
|
|
|
. |
||||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|||||||||||
|
|
15 1+ x2 |
||||||||||
5.10. y = 3 (1+ x3 4 )2 .
4 )2 .
x3 2
2
5.12. y = (x2 − 2)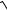
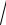 4 + x2 . 24x3
4 + x2 . 24x3
5.14. y = 
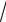 x −1(3x + 2). 4x2
x −1(3x + 2). 4x2
5.16. y = x6 + 8x3 −128. 8 − x3
5.18. y = (1− x2 )5 x3 + 1. x
x3 + 1. x
x −1
5.20. y = (x2 + 5)  x2 + 5 .
x2 + 5 .
5.22. y = 2 |
1− |
x |
|
. |
|
|
|
||
1+ |
x |
|||
5.24.y = 3 3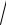 x2 + x +1. x +1
x2 + x +1. x +1
x + 7
5.26. y =  . 6
. 6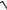 x2 + 2x + 7
x2 + 2x + 7
5.28. y = |
|
x2 + 2 |
|
|
. |
||
|
|
|
|
|
|||
|
|
|
|
|
|||
1− x |
4 |
||||||
2 |
|
|
|||||
5.30. y = 3x + 
 x .
x . 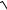
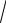 x2 + 2
x2 + 2
Задача 6. Найти производную.
6.1. y = x − ln(2 + ex + 2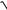
 e2x + ex +1).
e2x + ex +1).
6.3. y = 1 arctg ex − 3.
22
6.5.y = 2 ex +1 + ln 
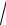 ex +1 −1.
ex +1 −1.
 ex +1 +1
ex +1 +1
6.7. y = 12 ln(e2x +1)− 2arctgex.
|
|
( |
|
− arctg |
|
) |
|
2 |
2x −1 |
2x −1 |
|||||
6.9. y = |
|
|
|
|
|
. |
|
|
|
|
|
|
|||
ln2
6.2. y = e2x (2 − sin2x − cos2x)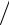 8.
8.
11+ 2x
6.4.y = ln4 ln1− 2x .
6.6. y = 23 
 (arctgex )3 .
(arctgex )3 .
6.8. y = ln |
( |
ex +1 + |
18e2x |
+ 27ex |
+11 |
. |
||||||||
|
|
|
|
|
|
|
|
|||||||
|
|
) |
|
|
( |
) |
3 |
|
|
|||||
|
|
|
|
|
6 |
|
|
|||||||
|
|
|
|
|
|
|
ex +1 |
|
|
|||||
|
|
|
|
|
|
|
|
|||||||
6.10. y = 2(x − 2) |
|
|
|
|
|
|
1+ ex |
−1 |
. |
|||||
1+ ex − 2ln |
|
|||||||||||||
|
|
|
|
|
||||||||||
|
|
|||||||||||||
|
|
|
|
|
|
|
|
1+ ex |
+1 |
|
||||
6.11. y = |
eαx (α sin β x − β cosβ x) |
6.12. y = |
eαx |
(β sin β x −α cosβ x) |
|
|||||||
|
|
|
|
|
. |
|
|
|
|
. |
||
|
|
α2 + β 2 |
|
|
|
α2 + β 2 |
||||||
|
|
|
|
|
|
|
|
|
||||
|
|
1 |
|
acos2bx + 2bsin2bx |
|
|
|
|
|
|||
6.13. y = eax |
|
+ |
|
|
|
. |
|
|
|
|
|
|
|
2(a2 |
+ 4b2 ) |
|
|
|
|
|
|||||
|
2a |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6.14. y = x + |
1 |
− ln(1+ ex ). |
|
||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
1+ ex |
|
||||
6.15. y = x − 3ln (1+ ex 6 )
6 )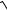
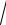 1+ ex
1+ ex 3 − 3arctgex
3 − 3arctgex 6.
6.
6.16. y = x + |
|
8 |
. |
|
+ ex 4 |
||
1 |
|
||
6.17. y = ln(ex + 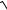
 e2x −1)+ arcsine−x.
e2x −1)+ arcsine−x.
6.18.y = x − e− x arcsinex − ln(1+ 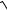
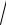 1− e2x ).
1− e2x ).
6.19.y = x − ln(1+ ex )− 2e−x 2 arctgex
2 arctgex 2 − (arctgex
2 − (arctgex 2 )2 .
2 )2 .
ex3
6.20. y = 1+ x3 .
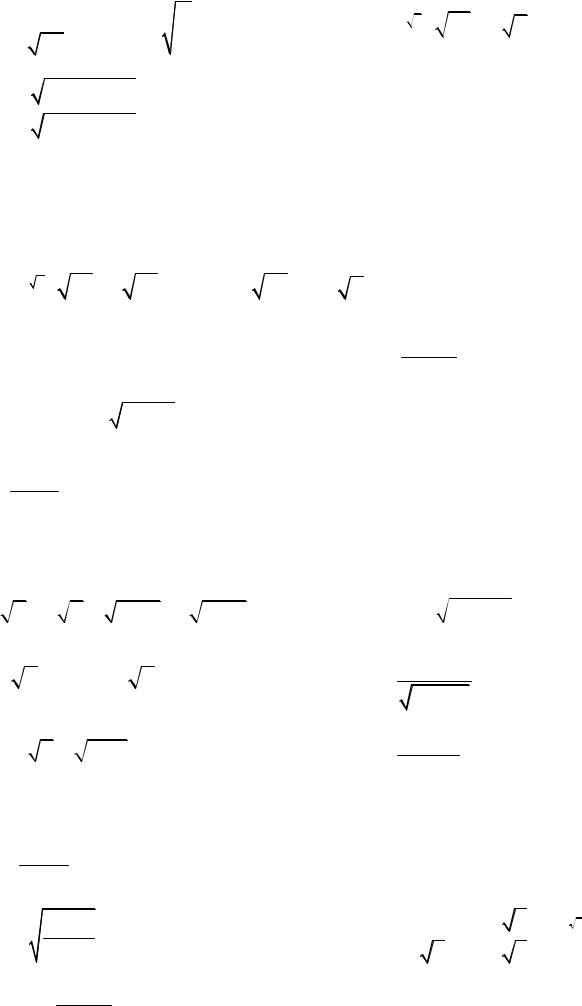
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1 |
|
|
|
|
|
a |
|
|
|||||||
6.21. y = |
|
|
|
|
|
|
|
arctg emx |
|
|
. |
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||||
|
m |
|
|
ab |
|
b |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
6.23. y = ln |
|
|
|
1+ ex + e2x − ex −1 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
1+ ex + e2x − ex +1 |
|
|
||||||||||
6.25. y = |
ex |
|
|
|
2 |
−1)cos x + (x −1) |
2 |
|
|||||||||
2 |
|
(x |
|
|
|
|
sin x . |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6.22. y = 3e3
 x (3
x (3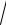 x2 − 23
x2 − 23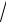 x + 2).
x + 2).
|
sin x |
1 |
|
6.24. y = e |
x − |
|
. |
|
|||
|
|
cos x |
|
6.26. y = arctg(ex − e−x ).
6.27. y = 3e3
 x (3
x (3 x5 − 53
x5 − 53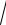 x4 + 20x − 603
x4 + 20x − 603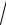 x2 +1203
x2 +1203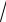 x −120).
x −120).
e3x
6.28. y = − 3sh3 x.
|
|
|
2 |
|
( |
|
) |
|
|
|
|
|
6.30. y = − |
1 |
e− x2 |
|
|
|
|
6.29. y = arcsine−x − 1− e2x . |
|
|
x4 + 2x2 + 2 |
|
. |
||||
ex2
6.31.y = 1+ x2 .
Задача 7. Найти производную.
7.1. y = 
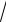 x ln(
x ln(
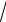 x +
x + 
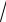 x + a )−
x + a )− 
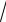 x + a.
x + a.
7.3. y = 2
 x − 4ln(2 +
x − 4ln(2 + 
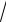 x ).
x ).
7.5. y = ln(
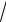 x +
x + 
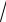 x +1).
x +1).
7.7. y = ln2 (x + cos x).
x2
7.9.y = ln1− x2 .
7.11. y = ln 4 1+ 2x. 1− 2x
2x + 4 7.13. y = lnsin x +1 .
7.2. y = ln(x + 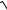
 a2 + x2 ).
a2 + x2 ).
7.4. y = ln x2 . 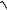 1− ax4
1− ax4
a2 + x2
7.6. y = ln a2 − x2 .
7.8. y = ln3 (1+ cos x).
|
π |
|
|
x |
|
|
|
|
||
7.10. y = lntg |
+ |
|
|
. |
|
|
|
|||
|
|
|
|
|||||||
|
4 |
|
|
2 |
|
|
|
|
||
|
|
|
|
x − |
|
|
|
|||
7.12. y = x + |
1 |
|
ln |
2 |
|
+ aπ |
||||
|
|
|
|
|
|
|||||
2 |
|
|
|
x + |
2 |
|
|
|||
7.14. y = log16 log5tg x.
 2
2
.
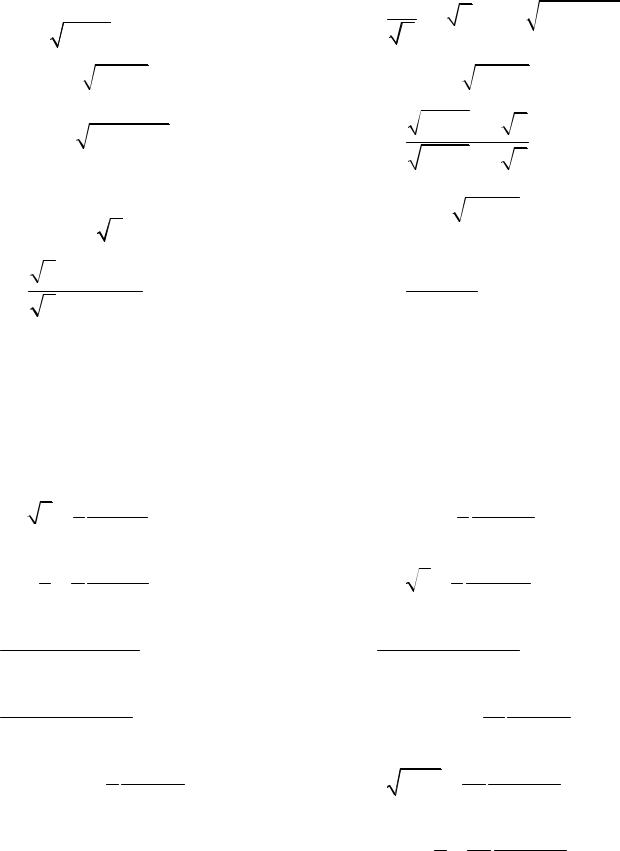
7.15. y = log4 log2tg x.
7.17. y = lncos |
2x + 3 |
. |
||||||
|
|
|
||||||
|
|
|
|
x +1 |
||||
7.19. y = log |
|
|
|
|
1 |
|
. |
|
|
|
|
|
|
|
|||
a |
|
|||||||
|
− x4 |
|||||||
|
1 |
|||||||
7.21. y = lnarcsin 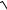
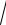 1− e2x .
1− e2x .
7.23. y = ln(bx + 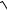
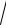 a2 + b2 x2 ).
a2 + b2 x2 ).
1
7.25.y = ln arccos .
.
x
7.27. y = ln 
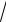 5 + tg(x
5 + tg(x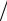 2).
2). 
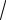 5 − tg(x
5 − tg(x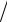 2)
2)
7.29. y = lnlnsin(1+1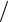 x).
x).
7.31. y = lnln2 ln3 x.
Задача 8. Найти производную.
8.1. y = sin 
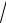 3 + 1 sin2 3x.
3 + 1 sin2 3x.
3cos6x
8.3.y = tglg 1 + 1 sin2 4x. 3 4 cos8x
8.5. y = cossin5 sin2 2x. 2cos4x
8.7. y = cosln7 sin2 7x. 7cos14x
8.9. y = ctg(cos2)+ 1 sin2 6x .
|
|
|
|
|
6 cos12x |
||||||
8.11. y = |
1 |
|
|
1 |
|
+ |
|
1 sin2 10x |
|||
|
|
cos tg |
|
|
|
|
|
|
. |
||
|
|
|
|
|
|||||||
|
3 |
|
2 |
|
|
10 cos20x |
|||||
7.16. y = x(cosln x + sinln x)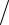 2.
2.
7.18. y = lgln(ctg x).
7.20. y = 12 ln(
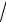 2 tg x +
2 tg x + 
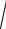 1+ 2tg2 x).
1+ 2tg2 x).
7.22. y = lnarccos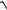
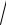 1− e4x .
1− e4x .
7.24. y = ln 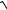
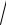 x2 +1 + x
x2 +1 + x
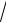 2 .
2 . 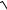
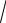 x2 +1 − x
x2 +1 − x
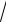 2
2
7.26. y = ln(ex + 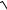
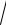 1+ e2x ).
1+ e2x ).
7.28. y = ln ln x . sin(1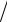 x)
x)
7.30. y = lnln3 ln2 x.
8.2. y = cosln2 − 1 cos2 3x.
3sin6x
8.4.y = ctg 3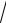 5 − 1 cos2 4x. 8 sin8x
5 − 1 cos2 4x. 8 sin8x
8.6. y = sincos3 cos2 2x. 4sin4x
8.8. y = cos(ctg2)− 1 cos2 8x. 16 sin16x
8.10. y = 3 ctg2 − 1 cos2 10x. 20 sin20x
8.12. y = lnsin 1 − 1 cos2 12x.
224 sin24x
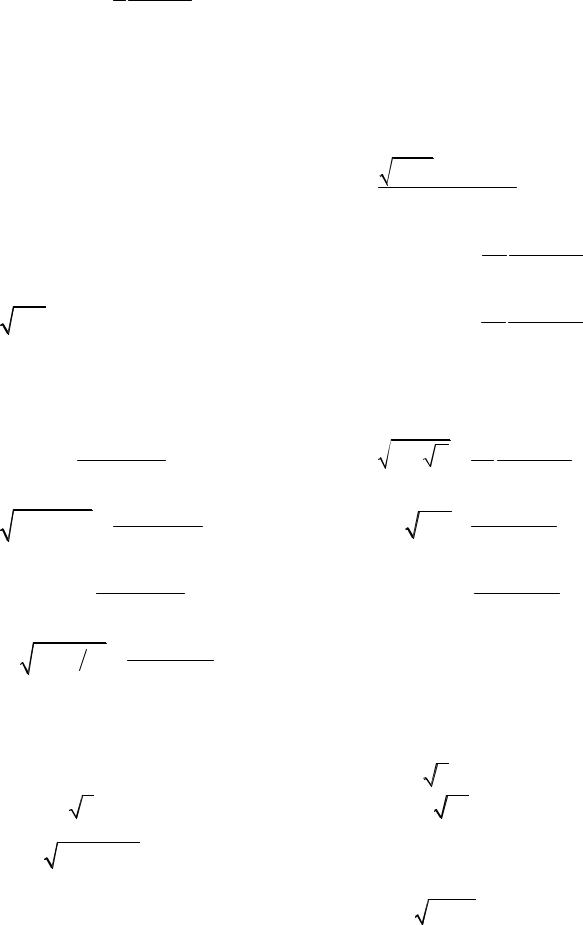
8.13. y = 8sin(ctg3)+ 1 sin2 5x . 5 cos10x
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|||||||||
|
cos tg |
|
|
|
sin |
|
|
15x |
|||||||||||||
|
|
|
|
|
|
||||||||||||||||
8.15. y = |
|
|
3 |
|
|
|
|
|
|
|
. |
||||||||||
|
15cos30x |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
1 |
|
|
sin |
2 |
|
|
|
|
|
|
|||||||
|
ctg sin |
|
|
|
|
|
|
|
17x |
||||||||||||
|
|
|
|
|
|
|
|||||||||||||||
8.17. y = |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
. |
|||||||
|
17cos34x |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
8.19. y = |
tg(ln2) sin2 19x |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
19cos38x |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
sin2 21x |
. |
|
|||||||||||
8.21. y = tg4 + |
|
|
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
21cos42x |
||||||||||||||
8.23. y = lncos |
1 |
+ |
|
sin2 23x |
. |
||||||||||||||||
|
|
|
|||||||||||||||||||
|
3 |
|
|
|
|
|
23cos46x |
||||||||||||||
8.25. y = sinln2 + sin2 25x . 25cos50x
8.27. y = 7 tg(cos2) + sin2 27x . 27cos54x
8.29. y = cos2 sin3+ sin2 29x . 29cos58x
8.31. y = tg cos(1 3) + sin2 31x . 31cos62x
Задача 9. Найти производную.
8.14. y = |
cos(ctg3) cos2 14x |
|||||||
|
|
|
|
|
|
|
. |
|
28sin28x |
|
|
||||||
|
|
|
|
|||||
|
|
1 |
cos |
2 |
|
|
|
|
|
sin tg |
|
|
|
16x |
|||
|
|
|
||||||
8.16. y = |
|
7 |
|
|
|
. |
||
|
|
|
|
|
|
|||
32sin32x
8.18. y = 5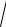 ctg2 cos2 18x. 36sin36x
ctg2 cos2 18x. 36sin36x
8.20. y = ctg(cos5)− 1 cos2 20x. 40 sin40x
8.22. y = cos(ln13)− 1 cos2 22x. 44 sin44x
|
1 |
|
|
|
1 cos2 24x |
||||
8.24. y = ctg sin |
|
|
|
|
− |
|
|
|
. |
|
|
|
|
|
|||||
|
13 |
|
|
48 sin48x |
|||||
8.26. y = 3 cos
cos
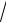 2 − 1 cos2 26x. 52 sin52x
2 − 1 cos2 26x. 52 sin52x
8.28. y = sin 3 tg2 − cos2 28x . 56sin56x
8.30. y = sin3 cos2 − cos2 30x . 60sin60x
9.1. y = arctg |
tg x − |
ctg x |
. |
|
|
|
|
9.2. y = arcsin |
|
|
x |
|
− |
2 |
. |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
5x |
||||||||||
|
2x −1 |
|
|
+ |
9 |
arcsin |
2x −1 |
. |
|
|
|
|
|
|
|
|
|
|
||||
9.3. y = |
|
2 + x − x2 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
4 |
|
|
|
|
|
|
8 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
9.4. y = arctg |
|
1+ x2 −1 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
x
