
Кузнецов_математика
.pdf
15.13. y′′ − y′ = 2ch x.
15.14.y′′ + 25y = 20cos5x −10sin5x + 50e5x .
15.15.y′′′ −16y′ = 48e4x + 64cos4x − 64sin4x.
15.16.y′′ + 2y′ = 2sh2x.
15.17.y′′ + 36y = 24sin6x −12cos6x + 36e6x .
15.18.y′′′ − 25y′ = 25(sin5x + cos5x) − 50e5x .
15.19.y′′ + 3y′ = 2sh3x.
15.20.y′′ + 49y =14sin7x + 7cos7x − 98e7x .
15.21.y′′′ − 36y′ = 36e6x − 72(cos6x + sin6x).
15.22.y′′ + 4y′ =16sh4x.
15.23.y′′ + 64y =16sin8x −16cos8x − 64e8x .
15.24.y′′′ − 49y′ =14e7x − 49(cos7x + sin7x).
15.25.y′′ + 5y′ = 50sh5x.
15.26.y′′ + 81y = 9sin9x + 3cos9x +162e9x .
15.27.y′′′ − 64y′ =128cos8x − 64e8x .
15.28.y′′ + y′ = 2sh x.
15.29.y′′ +100y = 20sin10x − 30cos10x − 200e10x .
15.30.y′′′ − 81y′ =162e9x + 81sin9x.
15.31.y′′′ −100y′ = 20e10x +100cos10x.
Задача 16. Найти решение задачи Коши.
16.1. |
y′′ +π 2 y = π 2 |
cosπ x, y(0) = 3, |
y′(0) = 0. |
|
16.2. |
y′′ + 3y′ = 9e3x |
(1 |
+ e3x ), y(0) = ln4, y′(0) = 3(1− ln2). |
|
16.3. |
y′′ + 4y = 8ctg2x, |
y(π 4) = 5, |
y′(π 4) = 4. |
|
16.4. |
y′′ − 6y′ + 8y = 4 (1+ e−2x ), y(0) =1+ 2ln2, y′(0) = 6ln2. |
|||

16.5. y′′ − 9y′ +18y = 9e3x |
(1+ e−3x ), |
|
y(0) = 0, |
y′(0) = 0. |
||||||||||||||||||||||||
16.6. y′′ +π 2 y = π 2 sinπ x =1, |
|
y(1 2), |
y′(1 2) = π 2 |
2. |
||||||||||||||||||||||||
16.7. y′′ + |
1 |
|
y |
= |
|
|
|
|
1 |
|
|
|
|
, |
y( |
0) = 2, |
y′(0) = 0. |
|
||||||||||
|
|
|
|
π 2 cos(x π ) |
|
|||||||||||||||||||||||
π 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
16.8. y′′ − 3y′ = |
|
|
|
9e−3x |
|
, |
y( |
0) = 4ln4, |
|
y′( |
0) = 3(3ln4 −1). |
|||||||||||||||||
|
|
3+ e−3x |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
16.9. y′′ + y = 4ctg x, |
y(π 2) = 4, |
y′(π 2) = 4. |
|
|
|
|||||||||||||||||||||||
16.10. y′′ − 6y′ + 8y = 4 ( |
2 + e−2x ), |
y(0) =1+ 3ln3, |
|
y′(0) =10ln3. |
||||||||||||||||||||||||
16.11. y′′ + 6y′ + 8y = 4e−2x |
(2 + e2x ), |
|
y(0) = 0, |
y′( |
0) = 0. |
|||||||||||||||||||||||
16.12. y′′ + 9y = 9 sin3x, |
|
y(π 6) = 4, |
|
y′(π 6) = 3π 2. |
||||||||||||||||||||||||
16.13. y′′ + 9y = 9 cos3x, |
y(0) =1, |
y′(0) = 0. |
|
|
|
|
||||||||||||||||||||||
16.14. y′′ − y′ = e− x (2 + e−x ), |
y(0) = ln27, |
y′(0) = ln9 −1. |
||||||||||||||||||||||||||
16.15. y′′ + 4y = 4ctg2x, |
y(π 4) = 3, |
|
y′(π 4) = 2. |
|
|
|||||||||||||||||||||||
16.16. y′′ − 3y′ + 2y = |
|
1 |
|
, |
|
y(0) =1+ 8ln2, |
|
y′( |
0) =14ln2. |
|||||||||||||||||||
3+ e− x |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
16.17. y′′ − 6y′ + 8y = 4e2x |
(1+ e−2x ), |
|
y(0) = 0, |
y′(0) = 0. |
||||||||||||||||||||||||
16.18. y′′ +16y =16 sin4x, |
y(π 8) = 3, |
y′(π 8) = 2π. |
||||||||||||||||||||||||||
16.19. y′′ +16y =16 cos4x, |
|
y( |
0) = 3, |
|
y′(0) = 0. |
|
|
|||||||||||||||||||||
16.20. y′′ − 2y′ = 4e−2x |
|
(1+ e−2x ), |
y( |
0) = ln4, |
y′(0) = ln4 − 2. |
|||||||||||||||||||||||
16.21. y′′ + |
y |
= |
1 |
ctg(x 2), |
|
y(π ) = 2, |
|
y′(π ) =1 2. |
|
|
||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
4 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
16.22. y′′ − 3y′ + 2y =1 |
|
(2 + e− x ), |
y( |
0) =1+ 3ln3, |
y′(0) = 5ln3. |
|||||||||||||||||||||||
16.23. y′′ + 3y′ + 2y = e−x |
( |
2 + ex ), |
y( |
0) = 0, |
y′(0) = 0. |
|||||||||||||||||||||||
16.24. y′′ + 4y = 4 sin2x, |
y(π 4) = 2, |
|
y′(π 4) = π. |
|
||||||||||||||||||||||||
16.25. y′′ + 4y = 4 cos2x, |
y( |
0) = 2, |
y′(0) = 0. |
|
|
|
||||||||||||||||||||||

16.26. |
y′′ + y′ = ex (2 + ex ), y(0) = ln27, y′(0) =1− ln9. |
|||
16.27. |
y′′ + y = 2ctg x, |
y(π 2) =1, |
y′(π 2) = 2. |
|
16.28. |
y′′ − 3y′ + 2y =1 (1+ e−x ), |
y(0) =1+ 2ln2, y′(0) = 3ln2. |
||
16.29. |
y′′ − 3y′ + 2y = ex |
(1+ e−x ), |
|
y(0) = 0, y′(0) = 0. |
16.30. |
y′′ + y =1 sin x, |
y(π 2) =1, |
y′(π 2) = π 2. |
|
16.31. |
y′′ + y =1 cos x, |
y(0) =1, |
y′(0) = 0. |
|

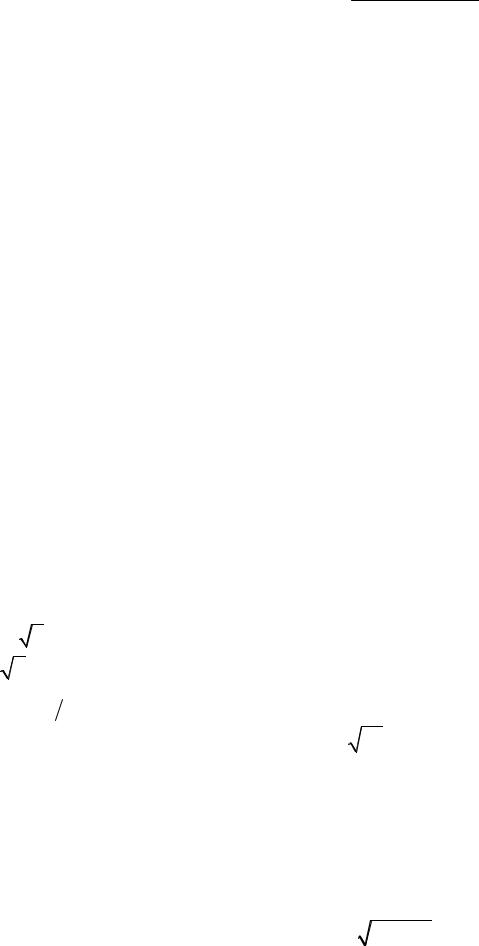




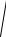 (
( n
n