Добавил:

Vezen Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Коломенский институт филиал МГМУ

Предмет:

Высшая математика

Файл:

Кузнецов_математика

.pdf

Скачиваний:

408

Добавлен:

20.06.2014

Размер:

2.87 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 2712 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>


6.21. 8xy′ −12y = −(5x2 + 3)y3,					y(1) =
						2.
6.22. 2(y′ + y) = xy2 ,		y(0) = 2.
6.23. y′ + xy = (x −1)ex y2 ,				y(0) =1.
6.24. 2y′ + 3ycos x = −e−2x (				2 + 3cos x) y−1, y(0) =1.
6.25. y′ − y = xy2 ,	y(	0) =1.
6.26. 2(xy′ + y) = y2 ln x,			y(1) = 2.
6.27. y′ + y = xy2 ,	y(	0) =1.
6.28. y′ + 2ycth x = y2 ch x,				y(1) =1 sh1.
6.29. 2(y′ + xy) = (x −1)ex			y2 , y(0) = 2.
6.30. y′ − ytg x = −(2 3)y4 sin x,					y(0) =1.
6.31. xy′ + y = xy2 ,	y(1) =1.

Задача 7. Найти общий интеграл дифференциального уравнения.

7.1. 3x2 ey dx + (x3 ey −1)dy = 0.

			2		2x		2x			2x
7.2.	3x2	+		cos		dx −			cos		dy = 0.
								2
			y		y		y			y

7.3. (3x2 + 4y2 )dx + (8xy + ey )dy = 0.

		y				1
7.4.	2x −1−			dx −	2y −		dy = 0.
		x	2
						x

7.5.(y2 + ysec2 x)dx + (2xy + tg x)dy = 0.

7.6.(3x2 y + 2y + 3)dx + (x3 + 2x + 3y2 )dy = 0.

7.7.

dx +

−

dy = 0.

+ y

x y

7.8. sin2x − 2cos(x + y) dx − 2cos(x + y)dy = 0.

7.9. (xy2 + x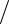y2 )dx + (x2 y − x2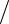y3 )dy = 0.

7.10.

dx −

dy = 0.

7.11.

cos

dx −

cos

+ 2y dy

= 0.

7.12.

+ y dx +

x +

dy = 0.

+ y

1+ xy

1− xy

x + y2

7.13.

dx +

dy = 0.

7.14.

−

dy = 0.

x2 y

xy2

xy +1

7.15.

−

= 0.

7.16. xe

dx −

dy = 0.

xcos y

7.17. 10xy −

dx +

5x2 +

− y2 sin y3

dy = 0.

sin y

sin

xdy

7.19. ey dx + (cos y + xey )dy = 0.

7.18.

+ ex

dx −

= 0.

+ y

7.20.(y3 + cos x)dx + (3xy2 + ey )dy = 0.

7.21.xey2 dx + (x2 yey2 + tg2 y)dy = 0.

7.22.(5xy2 − x3 )dx + (5x2 y − y)dy = 0.

7.23.cos(x + y2 )+ sin x dx + 2ycos(x + y2 )dy = 0.

7.24.(x2 − 4xy − 2y2 )dx + (y2 − 4xy − 2x2 )dy = 0.

7.25. sin y

+ ysin y +

+ xcos y − cos x +

dy = 0.

7.26. 1

ex y

dx + 1

−

ex y

dy = 0.

7.27.(x − y)dx + (x + y)dy = 0. x2 + y2

7.28.2(3xy2 + 2x3 )dx + 3(2x2 y + y2 )dy = 0.

7.29.(3x3 + 6x2 y + 3xy2 )dx + (2x3 + 3x2 y)dy = 0.

7.30.xy2dx + y(x2 + y2 )dy = 0.

7.31.xdx + ydy + (xdy − ydx)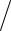(x2 + y2 ) = 0.

Задача 8. Для данного дифференциального уравнения методом изоклин построить интегральную кривую, проходящую через точку M .

8.1. y′ = y − x2 ,			M (1, 2).			8.2. yy′ = −2x,				M (0, 5).
8.3. y′ = 2 + y2 ,			M (1, 2).			8.4. y′ =	2x	,	M (1, 1).

							3y
8.5. y′ = (y −1)x,				M (1, 3 2).		8.6. yy′ + x = 0,				M (−2,	− 3).
8.7. y′ = 3+ y2 ,			M (1, 2).			8.8. xy′ = 2y,			M (2, 3).
8.9. y′(x2 + 2)= y,				M (2, 2).		8.10. x2 − y2 + 2xyy′ = 0,					M (2, 1).
8.11. y′ = y − x,			M (9 2, 1).			8.12. y′ = x2 − y,				M (1,	1 2).
8.13. y′ = xy,		M (0, −1).				8.14. y′ = xy,			M (0, 1).
8.15. yy′ = −	x	,	M (4, 2).			8.16. 2(y + y′) = x + 3,					M (1, 1 2).

2
8.17. y′ = x + 2y,				M (3, 0).		8.18. xy′ = 2y,			M (1, 3).
8.19. 3yy′ = x,		M (−3,			− 2).	8.20. y′ = y − x2 ,				M (−3, 4).
8.21. x2 − y2 + 2xyy′ = 0,					M (−2, 1).	8.22. y′ = x2 − y,				M (2,	3 2).
8.23. y′ = y − x,			M (2, 1).			8.24. yy′ = −x,			M (2, 3).
8.25. y′ = y − x,			M (4, 2).			8.26. 3yy′ = x,			M (1, 1).
8.27. y′ = x2 − y,			M (0, 1).			8.28. y′ = 3y2 3,				M (1, 3).
8.29. x2 − y2 + 2xyy′ = 0,					M (−2, −1).	8.30. y′ = x(y −1), M (1, 1 2).
8.31. y′ = x + 2y,				M (1,	2).

Задача 9. Найти линию, проходящую через точку M0 и обладающую тем

свойством, что в любой ее точке M нормальный вектор MN с концом на оси Oy имеет длину, равную a, и образует острый угол с положительным направлением оси Oy.

9.1. M0	(15, 1),	a = 25.	9.2. M0	(12, 2),	a = 20.
9.3. M0	(9, 3),	a =15.	9.4. M0	(6, 4),	a =10.
9.5. M0	(3, 5),	a = 5.

Найти линию, проходящую через точку M0 , если отрезок любой ее касательной между точкой касания и осью Oy делится в точке пересечения с осью абсцисс в отношении a:b (считая от оси Oy).

9.6. M0	(1, 1),	a :b =1:2.	9.7. M0	(−2, 3),	a :b =1:3.
9.8. M0	(0, 1),	a:b = 2:3.	9.9. M0	(1, 0),	a:b = 3:2.
9.10. M0 (2, −1), a :b = 3:1.

9.11. M0	(2, −1),	a:b =1:1.	9.12. M0 (1, 2),	a:b = 2:1.
9.13. M0	(−1, 1),	a :b = 3:1.	9.14. M0 (2, 1),	a :b =1:2.
9.15. M0	(1, −1),	a:b =1:3.

Найти линию, проходящую через точку M0 , если отрезок любой ее касательной, заключенный между осями координат, делится в точке касания в отношении a:b

(считая от оси Oy).

9.16. M0	(1,	2),	a:b =1:1.	9.17. M0 (2,	1), a :b =1:2.
9.18. M0	(1,	3), a:b = 2:1.		9.19. M0 (2,	− 3), a :b = 3:1.
9.20. M0	(3, −1),		a :b = 3:2.

Найти линию, проходящую через точку M0 и обладающую тем свойством, что в

любой ее точке M касательный вектор MN с концом на оси Ox имеет проекцию на ось

Ox, обратно пропорциональную абсциссе точки M . Коэффициент пропорциональности

равен a.
9.21. M0 (1,		e),		a = −1 2.		9.22. M0 (2,	e),	a = −2.
	(−1,			),	a = −1.	9.24. M0 (2,	1 e),	a = 2.
9.23. M0	(−1,		e	),	a = −1.	9.24. M0 (2,	1 e),	a = 2.
9.25. M0	(1,	1 e2 ),			a =1 4.

Найти линию, проходящую через точку M0 и обладающую тем свойством, что в

любой ее точке M касательный вектор MN с концом на оси Oy имеет проекцию на ось

Oy, равную a.

9.26. M0 (1, 2),		a = −1.	9.27. M0	(1, 4),		a = 2.
9.28. M0 (1,	5),	a = −2.	9.29. M0	(1,	3),	a = −4.
9.30. M0 (1,	6),	a = 3.	9.31. M0	(1,	1),	a =1.

Задача 10. Найти общее решение дифференциального уравнения.

10.1. y′′′xln x = y′′. 10.3. 2xy′′′ = y′′.

10.5. tg x y′′ − y′ + 1 = 0. sin x

10.7. y′′′ctg2x + 2y′′ = 0.

10.9. tg x y′′′ = 2y′′.

10.11. x4 y′′ + x3 y′ =1.

10.13. (1+ x2 )y′′ + 2xy′ = x3.

10.15. xy′′′ − y′′ + 1 = 0. x

10.17. th x yIV = y′′′. 10.19. y′′′tg x = y′′ +1.

10.21. y′′′th7x = 7y′′.

10.2. xy′′′ + y′′ =1. 10.4. xy′′′ + y′′ = x +1.

10.6. x2 y′′ + xy′ =1.

10.8.x3 y′′′ + x2 y′′ =1.

10.10.y′′′cth2x = 2y′′.

10.12. xy′′′ + 2y′′ = 0.

10.14. x5 y′′′ + x4 y′′ =1.

10.16. xy′′′ + y′′ + x = 0.

10.18. xy′′′ + y′′ = x.

10.20. y′′′tg5x = 5y′′.

10.22. x3 y′′′ + x2 y′′ = x.

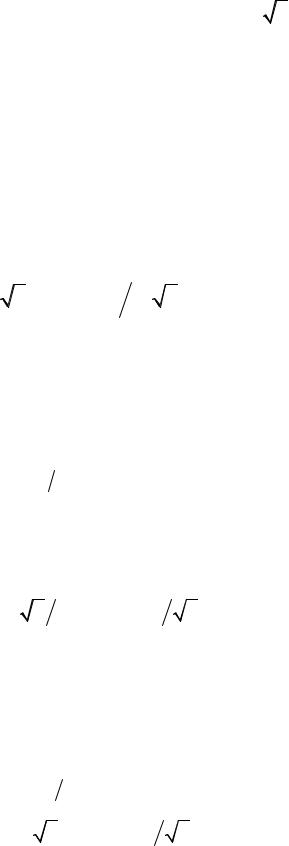
10.23. cth x y′′ − y′ +

= 0.

10.24. (x +1)y′′′ + y′′ = (x +1).

ch x

10.25. (1+ sin x)y

′′′

′′

′′′

+ y

′′

= cos x y .

10.26. xy

10.27. −xy′′′ + 2y′′ =

10.28. cth xy′′ + y′ = ch x.

10.29. x4 y′′ + x3 y′ = 4.

10.30. y′′ +

y′ = 2x.

x2 +1

10.31. (1+ x2 )y′′ + 2xy′ =12x3.

Задача 11. Найти решение задачи Коши.

11.1. 4y3 y′′ = y4 −1,

0) =

y′(0) =1 (2

11.2. y′′ =128y3,

0) =1,

y′(0) = 8.

′′ 3

+ 64 = 0,

y(0) = 4,

′

(0) = 2.

11.3. y y

11.4. y′′ + 2sin ycos3 y = 0,

0) = 0,

y′(0) =1.

11.5. y′′ = 32sin3 ycos y,

y(1) = π 2,

y′(1) = 4.

11.6. y′′ = 98y3,

y(1) =1,

y′(1) = 7.

′′ 3

+ 49 = 0,

y(3) = −7,

′

(

3) = −1.

11.7. y y

11.8. 4y3 y′′ =16y4 −1, y(

0) =

y′(0) =1

11.9. y′′ + 8sin ycos3 y = 0,

y(0) = 0,

y′(0) = 2.

11.10. y′′ = 72y3,

2) =1,

y′(2) = 6.

′′

+ 36 = 0,

0) =

′

(0) = 2.

11.11. y y

11.12. y′′ =18sin3 ycos y,

y(1) = π 2,

y′(1) = 3.

11.13. 4y3 y′′ = y4 −16,

y(0) = 2

y′(0) =1

11.14. y′′ = 50y3,

3) =1,

y′(3) = 5.

′′

+ 25 = 0,

2) = −5,

′

(2) = −1.

11.15. y y

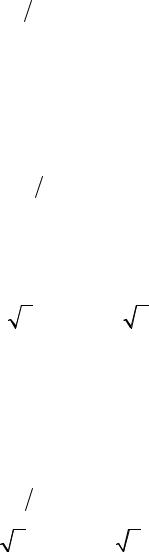
11.16. y′′

+18sin ycos3 y = 0,

y(0) = 0,

y′(0) = 3.

11.17. y′′

= 8sin3 ycos y,

y(1) = π 2,

y′(1) = 2.

11.18. y′′ = 32y3,

4) =1,

y′(

4) = 4.

′′

+16 = 0,

y(1) = 2,

′

(1) = 2.

11.19. y y

11.20. y′′ + 32sin ycos3 y = 0,

y(0) = 0,

y′(0) = 4.

11.21. y′′ = 50sin3 ycos y,

y(1) = π 2,

y′(1) = 5.

11.22. y′′ =18y3,

y(1) =1,

y′(1) = 3.

′′

+ 9

= 0,

y(1) =1,

′

(1) = 3.

11.23. y y

11.24. y3 y′′ = 4

(y4 −1),

y(0)

y′(0) =

11.25. y′′ + 50sin ycos3 y = 0,

y(0) = 0,

y′(0) = 5.

11.26. y′′ = 8y3,

y(0) =1,

y′(0) = 2.

′′

+ 4

= 0, y(0) = −1,

′

(0) = −2.

11.27. y y

11.28. y′′ = 2sin3 ycos y,

y(1) = π 2,

y′(1) =1.

11.29. y3 y′′ = y4 −16,

y(0) = 2

2, y′(0) = 2.

11.30. y′′ = 2y3,

y(−1) =1,

y′(−1) =1.

′′

+1= 0,

y(1) = −1,

′

(1) = −1.

11.31. y y

Задача 12. Найти общее решение дифференциального уравнения.

12.1. y′′′ + 3y′′ + 2y′ =1− x2.	12.2. y′′′ − y′′ = 6x2 + 3x.
12.3. y′′′ − y′ = x2 + x.	12.4. yIV − 3y′′′ + 3y′′ − y′ = 2x.
12.5. yIV − y′′′ = 5(x + 2)2 .	12.6. yIV − 2y′′′ + y′′ = 2x(1− x).
12.7. yIV + 2y′′′ + y′′ = x2 + x −1.	12.8. yV − yIV = 2x + 3.
12.9. 3yIV + y′′′ = 6x −1.	12.10. yIV + 2y′′′ + y′′ = 4x2.
12.11. y′′′ + y′′ = 5x2 −1.	12.12. yIV + 4y′′′ + 4y′′ = x − x2.

12.13. 7y′′′ − y′′ =12x.	12.14. y′′′ + 3y′′ + 2y′ = 3x2 + 2x.
12.15. y′′′ − y′ = 3x2 − 2x +1.	12.16. y′′′ − y′′ = 4x2 − 3x + 2.
12.17. yIV − 3y′′′ + 3y′′ − y′ = x − 3.	12.18. yIV + 2y′′′ + y′′ =12x2 − 6x.
12.19. y′′′ − 4y′′ = 32 − 384x2.	12.20. yIV + 2y′′′ + y′′ = 2 − 3x2.
12.21. y′′′ + y′′ = 49 − 24x2.	12.22. y′′′ − 2y′′ = 3x2 + x − 4.
12.23. y′′′ −13y′′ +12y′ = x −1.	12.24. yIV + y′′′ = x.
12.25. y′′′ − y′′ = 6x + 5.	12.26. y′′′ + 3y′′ + 2y′ = x2 + 2x + 3.
12.27. y′′′ − 5y′′ + 6y′ = (x −1)2 .	12.28. yIV − 6y′′′ + 9y′′ = 3x −1.
12.29. y′′′ −13y′′ +12y′ =18x2 − 39.	12.30. yIV + y′′′ =12x + 6.
12.31. y′′′ − 5y′′ + 6y′ = 6x2 + 2x − 5.

Задача 13. Найти общее решение дифференциального уравнения.

13.1.y′′′ − 4y′′ + 5y′ − 2y = (16 −12x)e−x .

13.2.y′′′ − 3y′′ + 2y′ = (1− 2x)ex .

13.3.y′′′ − y′′ − y′ + y = (3x + 7)e2x .

13.4.y′′′ − 2y′′ + y′ = (2x + 5)e2x .

13.5.y′′′ − 3y′′ + 4y = (18x − 21)e−x .

13.6.y′′′ − 5y′′ + 8y′ − 4y = (2x − 5)ex .

13.7.y′′′ − 4y′′ + 4y′ = (x −1)ex .

13.8.y′′′ + 2y′′ + y′ = (18x + 21)e2x .

13.9.y′′′ + y′′ − y′ − y = (8x + 4)ex .

13.10.y′′′ − 3y′ − 2y = −4x ex .

13.11.y′′′ − 3y′ + 2y = (4x + 9)e2x .

13.12.y′′′ + 4y′′ + 5y′ + 2y = (12x +16)ex .

13.13.y′′′ − y′′ − 2y′ = (6x −11)e−x .

13.14. y′′′ + y′′ − 2y′ = (6x + 5)ex .

13.15.y′′′ + 4y′′ + 4y′ = (9x +15)ex .

13.16.y′′′ − 3y′′ − y′ + 3y = (4 − 8x)ex .

13.17.y′′′ − y′′ − 4y′ + 4y = (7 − 6x)ex .

13.18.y′′′ + 3y′′ + 2y′ = (1− 2x)e−x .

13.19.y′′′ − 5y′′ + 7y′ − 3y = (20 −16x)e−x .

13.20.y′′′ − 4y′′ + 3y′ = −4x ex .

13.21.y′′′ − 5y′′ + 3y′ + 9y = (32x − 32)e−x .

13.22.y′′′ − 6y′′ + 9y′ = 4x ex .

13.23.y′′′ − 7y′′ +15y′ − 9y = (8x −12)ex .

13.24.y′′′ − y′′ − 5y′ − 3y = −(8x + 4)ex .

13.25.y′′′ + 5y′′ + 7y′ + 3y = (16x + 20)ex .

13.26.y′′′ − 2y′′ − 3y′ = (8x −14)e−x .

13.27.y′′′ + 2y′′ − 3y′ = (8x + 6)ex .

13.28.y′′′ + 6y′′ + 9y′ = (16x + 24)ex .

13.29.y′′′ − y′′ − 9y′ + 9y = (12 −16x)ex .

13.30.y′′′ + 4y′′ + 3y′ = 4(1− x)e−x .

13.31.y′′′ + y′′ − 6y′ = (20x +14)e2x .

Задача 14. Найти общее решение дифференциального уравнения.

14.1.	y′′ + 2y′ = 4ex (sin x + cos x).	14.2. y′′ − 4y′ + 4y = −e2x sin6x.
14.3.	y′′ + 2y′ = −2ex (sin x + cos x).	14.4. y′′ + y = 2cos7x + 3sin7x.
14.5.	y′′ + 2y′ + 5y = −sin2x.	14.6. y′′ − 4y′ + 8y = ex (5sin x − 3cos x).
14.7.	y′′ + 2y′ = ex (sin x + cos x).	14.8. y′′ − 4y′ + 4y = e2x sin3x.

14.9. y′′ + 6y′ +13y = e−3x cos4x.	14.10. y′′ + y = 2cos3x − 3sin3x.
14.11. y′′ + 2y′ + 5y = −2sin x.	14.12. y′′ − 4y′ + 8y = ex (−3sin x + 4cos x).
14.13. y′′ + 2y′ =10ex (sin x + cos x).	14.14. y′′ − 4y′ + 4y = e2x sin5x.
14.15. y′′ + y = 2cos5x + 3sin5x.	14.16. y′′ + 2y′ + 5y = −17sin2x.
14.17. y′′ + 6y′ +13y = e−3x cos x.	14.18. y′′ − 4y′ + 8y = ex (3sin x + 5cos x).
14.19. y′′ + 2y′ = 6ex (sin x + cos x).	14.20. y′′ − 4y′ + 4y = −e2x sin4x.
14.21. y′′ + 6y′ +13y = −e3x cos5x.	14.22. y′′ + y = 2cos7x − 3sin7x.
14.23. y′′ + 2y′ + 5y = −cos x.	14.24. y′′ − 4y′ + 8y = ex (2sin x − cos x).
14.25. y′′ + 2y′ = 3ex (sin x + cos x).	14.26. y′′ − 4y′ + 4y = e2x sin4x.
14.27. y′′ + 6y′ +13y = e−3x cos8x.	14.28. y′′ + 2y′ + 5y =10cos x.
14.29. y′′ + y = 2cos4x + 3sin4x.	14.30. y′′ − 4y′ + 8y = ex (−sin x + 2cos x).
14.31. y′′ − 4y′ + 4y = e2x sin6x.

Задача 15. Найти общее решение дифференциального уравнения.

15.1.y′′ − 2y′ = 2ch2x.

15.2.y′′ + y = 2sin x − 6cos x + 2ex .

15.3.y′′′ − y′ = 2ex + cos x.

15.4.y′′ − 3y′ = 2ch3x.

15.5.y′′ + 4y = −8sin2x + 32cos2x + 4e2x .

15.6.y′′′ − y′ =10sin x + 6cos x + 4ex .

15.7.y′′ − 4y′ =16ch4y.

15.8.y′′ + 9y = −18sin3x −18e3x .

15.9.y′′′ − 4y′ = 24e2x − 4cos2x + 8sin2x.

15.10.y′′ − 5y′ = 50ch5x.

15.11.y′′ +16y =16cos4x −16e4x .

15.12.y′′′ − 9y′ = −9e3x +18sin3x − 9cos3x.

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 2712 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете Высшая математика

#
20.06.2014380.9 Кб75Доказательства по линейной алгебре.docx
#
20.06.20142.87 Mб408Кузнецов_математика.pdf
#
20.06.2014951.81 Кб526Ответы на вопросы к экзамену по математике (шпаргалки).doc
#
20.06.20142.31 Mб175ТПУ Линейная алгебра 1курс ИДЗ №1.doc
#
20.06.2014380.42 Кб63ТПУ Линейная алгебра 1курс ИДЗ №2.doc
#
20.06.2014539.14 Кб56ТПУ Линейная алгебра 1курс ИДЗ №3.doc
#
20.06.20141.09 Mб65ТПУ Линейная алгебра 1курс ИДЗ №4.doc