ТПУ Линейная алгебра 1курс ИДЗ №3

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«Национальный исследовательский Томский политехнический Университет»

Институт

дистанционного образования

линейная алгебра

Индивидуальное домашнее задание № 3

_{вариант №1}

по дисциплине:

Линейная алгебра и аналитическая геометрия

Исполнитель:
студент группы					16.12.2013
Руководитель:
преподаватель			.

Томск  2013

Индивидуальное задание 3

Вариант 1

Задача 1. Составить уравнения прямых, проходящих через точку A(-3;2)

a) параллельно прямой 2x + 5y + 4 = 0 ;

b) перпендикулярно прямой

c) под углом 45 к прямой y - 2 = 0;

d) через две точки: A(-3;2) и B(7;-5).

Построить эти прямые в системе координат. Записать вектор нормали N, направляющий вектор s и угловой коэффициент k для каждой прямой.

Решение

1. Вектор нормали данной прямой 2x + 5y + 4 = 0

. Так как искомая прямая параллельна данной, то вектор нормали также является вектором нормали искомой прямой. Также дана точка на искомой прямой A(-3;2)

Воспользуемся уравнением прямой через точку M0(x0; y0) с нормальным вектором

A(x - x0) + B(y - y0) = 0

Для полученной прямой:

• Вектор нормали

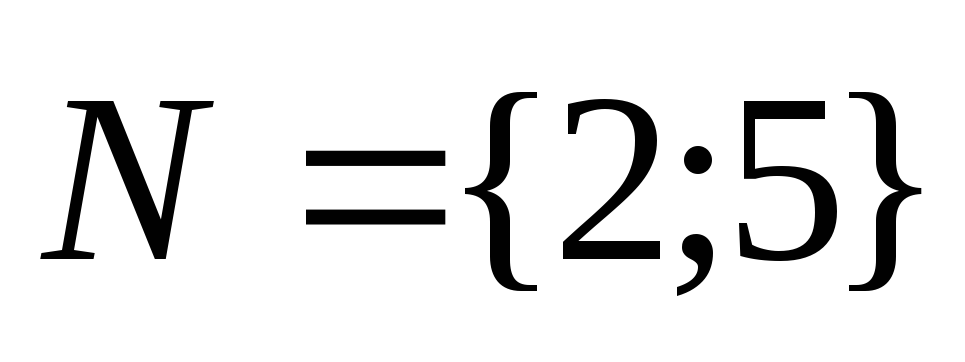
• Направляющий вектор (надо поменять местами координаты вектора нормали и у одной сменить знак)

• Угловой коэффициент (надо записать уравнение в виде y=kx+b)

2. Прямая задана в канонической форме и ее направляющий вектор s1 ={4;-1} . Он может служить вектором нормали искомой прямой, т.к. прямые перпендикулярны. Таким образом, имея точку (-3; 2) и вектор нормали записываем уравнение прямой

Для полученной прямой

• Вектор нормали

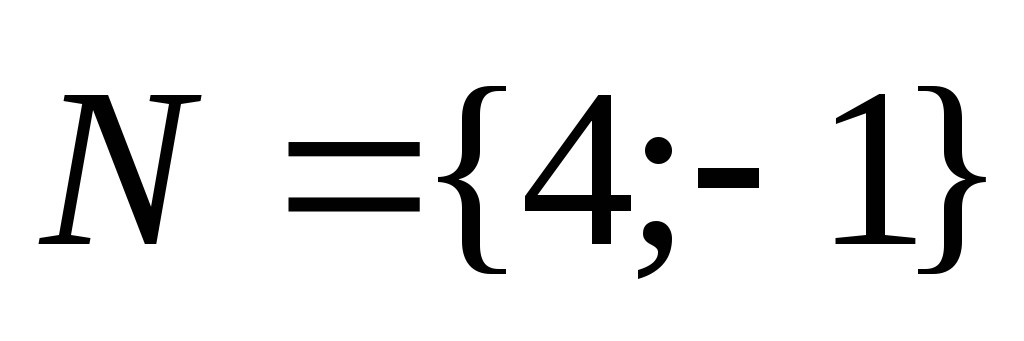
• Направляющий вектор

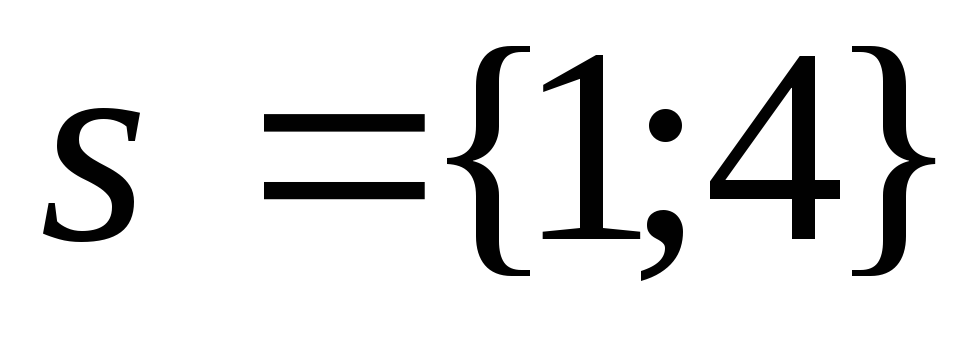
• Угловой коэффициент

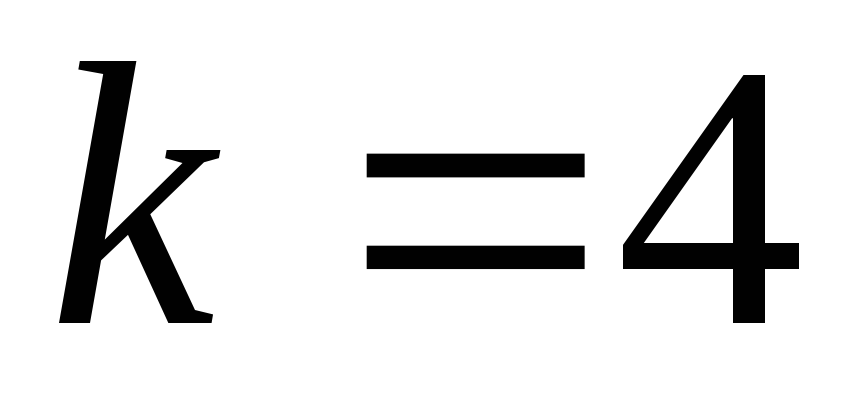
3. Данная прямая y - 2 = 0 является горизонтальной и составляет с осью OX угол 0 . Под углом к ней через заданную точку можно провести две прямые, одна прямая будет составлять с осью OX угол и, следовательно, ее угловой коэффициент 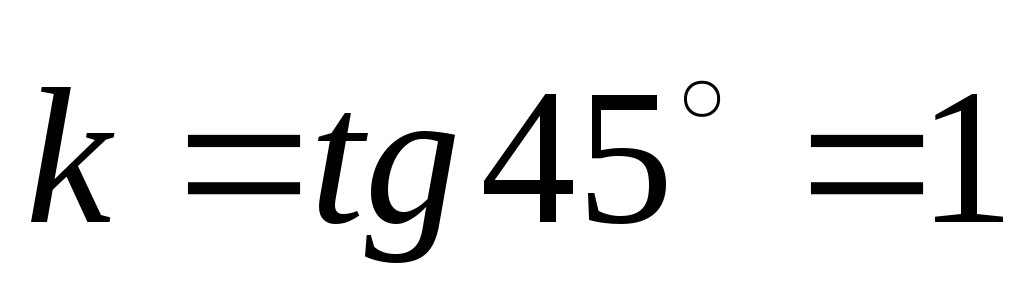, а другая прямая будет составлять с осью OX угол 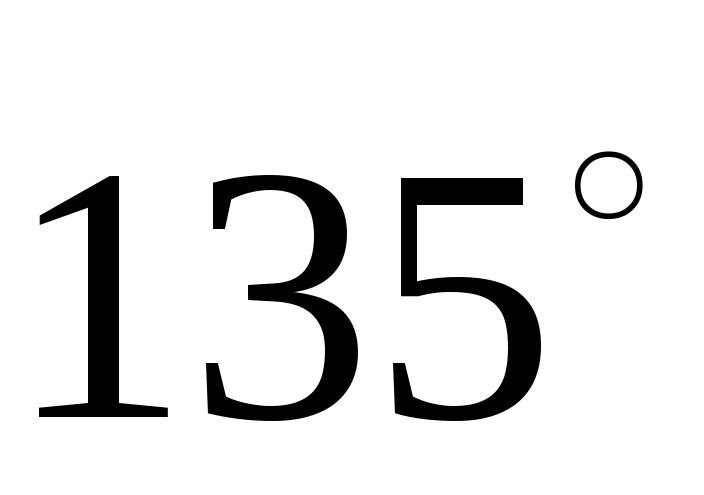и, следовательно, ее угловой коэффициент 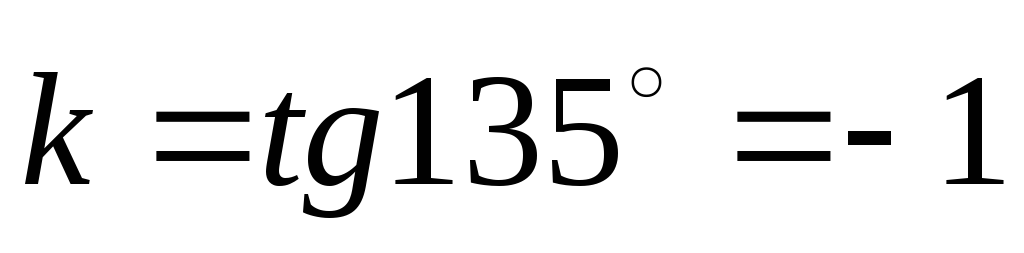. Используем уравнение прямой через точку с угловым коэффициентом

Для полученных прямых

• Вектор нормали

• Направляющий вектор

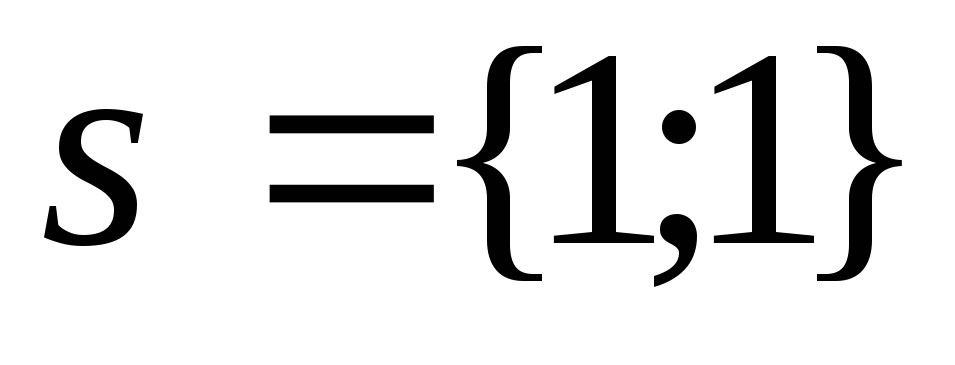
• Угловой коэффициент

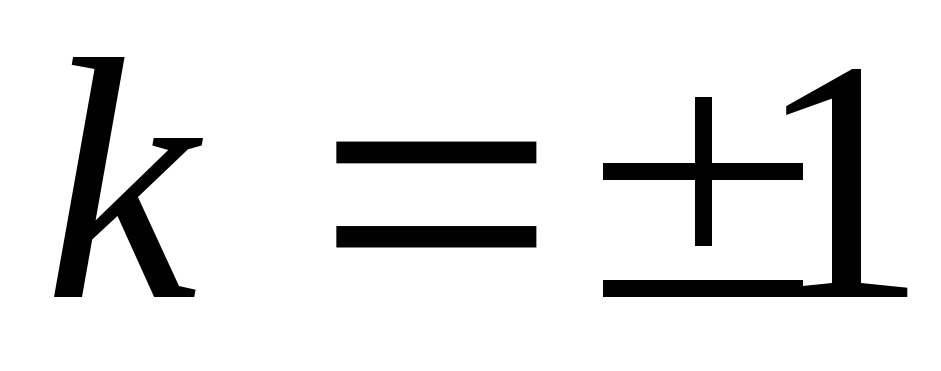
4. Уравнение прямой, проходящей через 2 точки

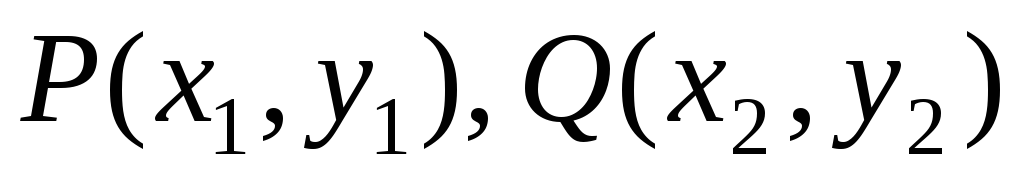
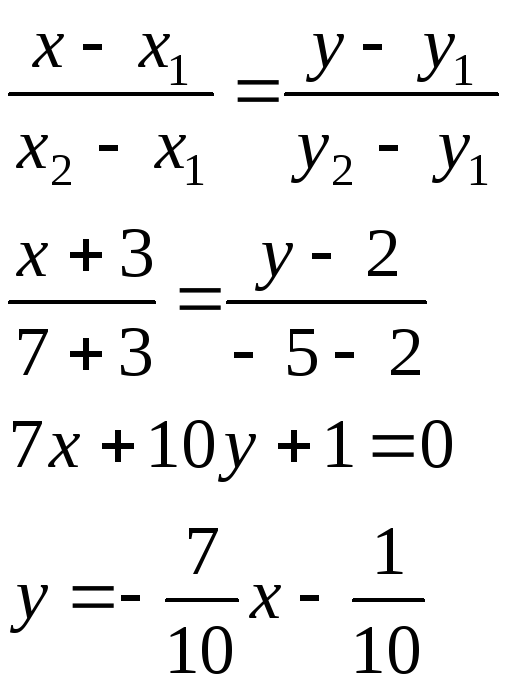
Для полученной прямой

• Вектор нормали

• Направляющий вектор

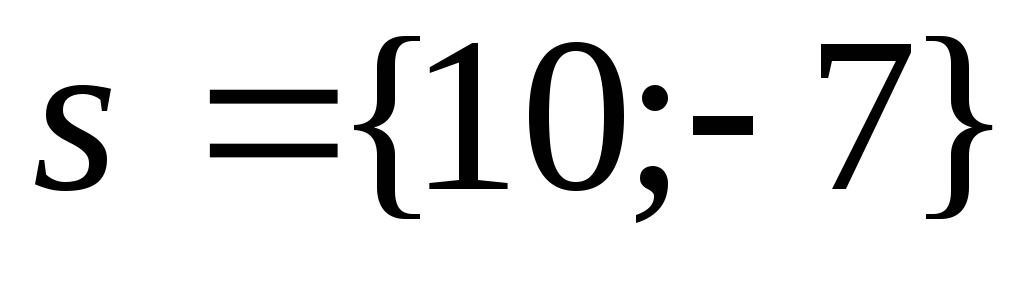
• Угловой коэффициент

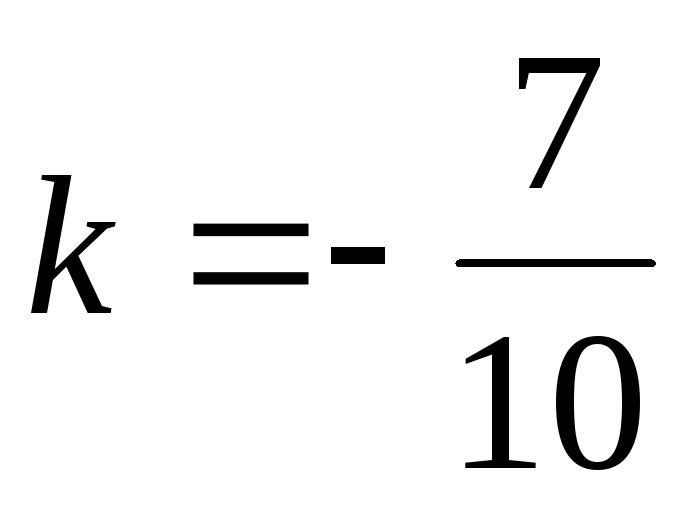
Расчетная таблица для построения прямых :

Уравнение прямой	x=0	y=0
	y=4/5	x=2
	y=14	x=-7/2
	y=5	x=-5
	y=-1	x=-1
	y=-1/10	x=-1/7

Задача 2. Даны две прямые

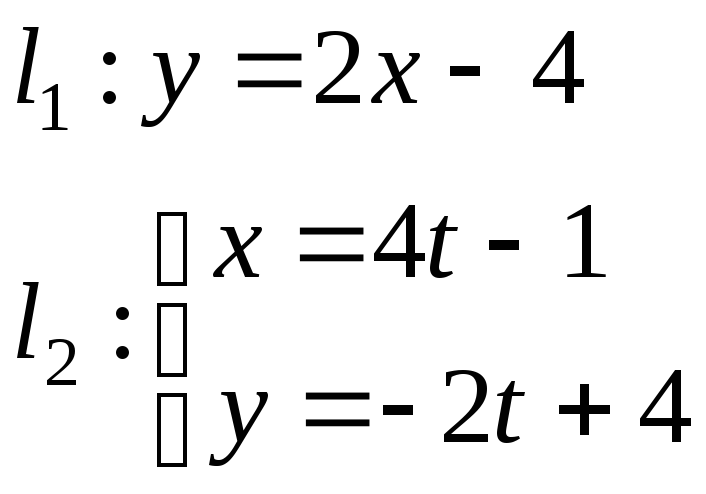
Найти:

a) точку пересечения прямых,

b) косинус угла между прямыми,

c) расстояния от точки M(6;-4) до прямой l1 и до прямой l2 .

Решение:

a) Точкой пересечения прямых является решение системы

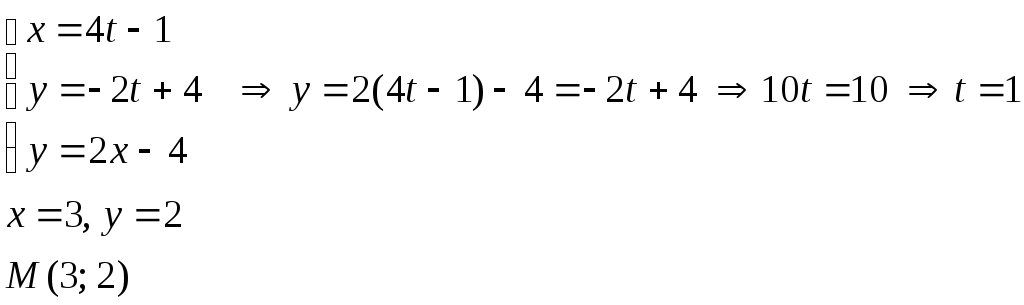
b) Косинус угла между прямыми найдем как косинус угла между их нормальными векторами:

Для

Для известен направляющий вектор

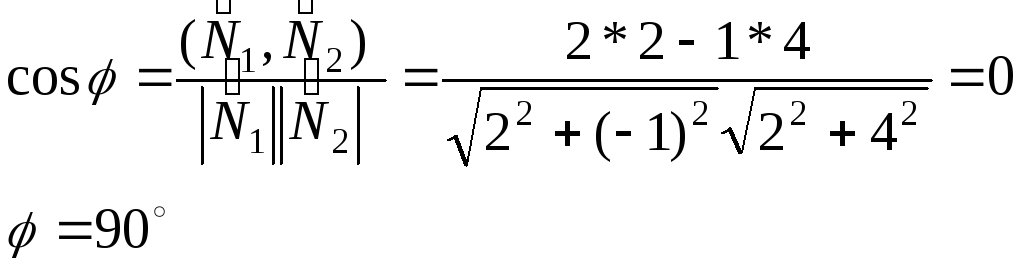
c) Для вычисления расстояния от точки M1(x1; y1) до прямой Ax + By + C = 0 воспользуемся формулой:

Расстояние до первой прямой

Для нахождения расстояния до второй прямой необходимо сначала привести уравнение l2 к общему виду

Вновь используем формулу расстояния от точки до прямой

Задача 3. Привести уравнения линий к каноническому виду и построить:

1)

2)

3)

4)

Решение:

1)

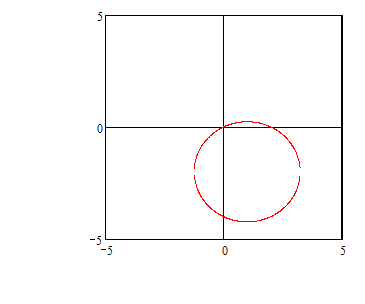
Полученное уравнение определяет окружность с центром и радиусом

2)

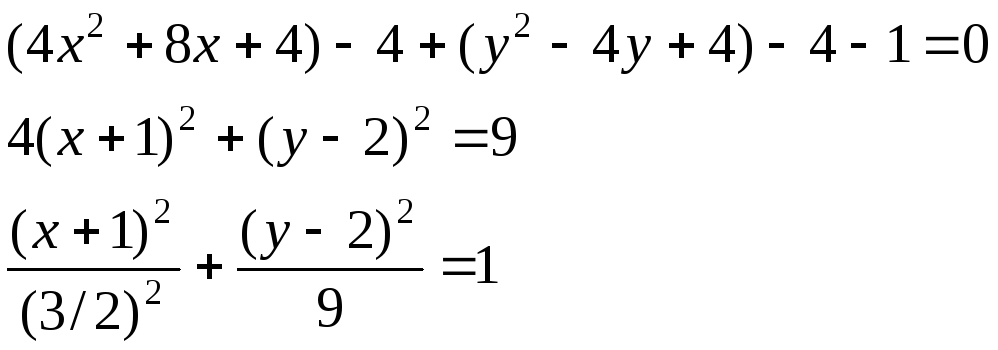
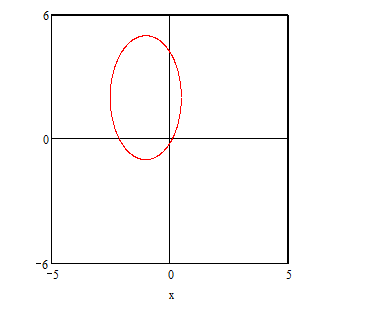
Полученное уравнение определяет эллипс с центром и полуосями

3)

Полученное выражение определяет мнимую гиперболу с центром , действительной полуосью и мнимой полуосью . Однако исходное уравнение ( определяет только верхнюю ветвь этой гиперболы

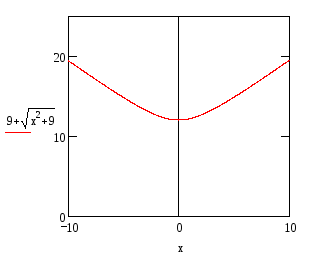
4)

Это уравнение определяет параболу с вершиной , ось которой параллельлная оси ОХ и ветви направлены влево.

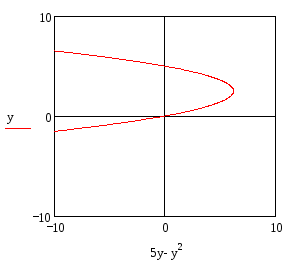
Задача 4. Построить линии, заданные уравнениями в полярных координатах:

1)

2)

Решение:

1)

Данная функция не обладает четностью и нечетностью, имеет период и область определения

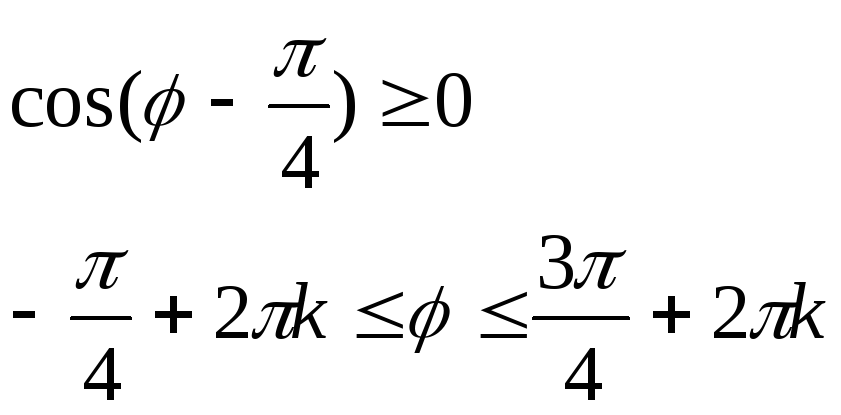
График функции не симметричен относительно осей координат, однако относительно прямой он симметричен.

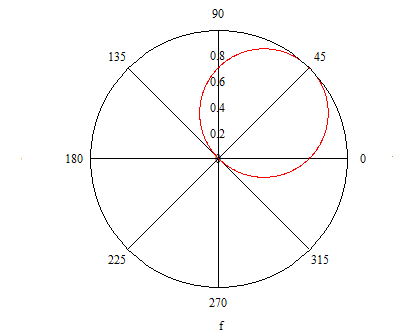
Находим несколько значений функции в интервале и достраиваем функцию с учетом симметрии

	1		0

2)

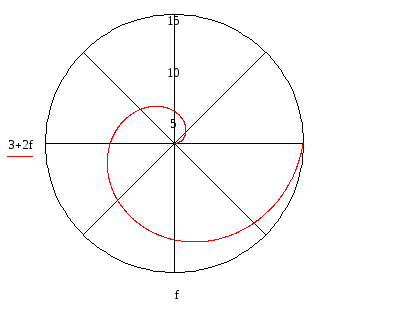
Данная функция не обладает четностью и нечетностью, не имеет периода и имеет область определения

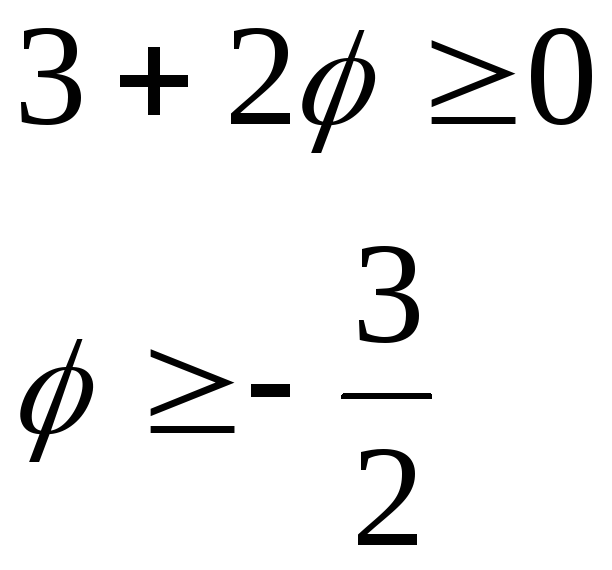
График функции не симметричен относительно осей координат

Найдем несколько значений функции

				0		1		2
	0	1	2	3	4	5	6	7	8

Задача 5. Построить линии, заданные параметрическими уравнениями:

1)

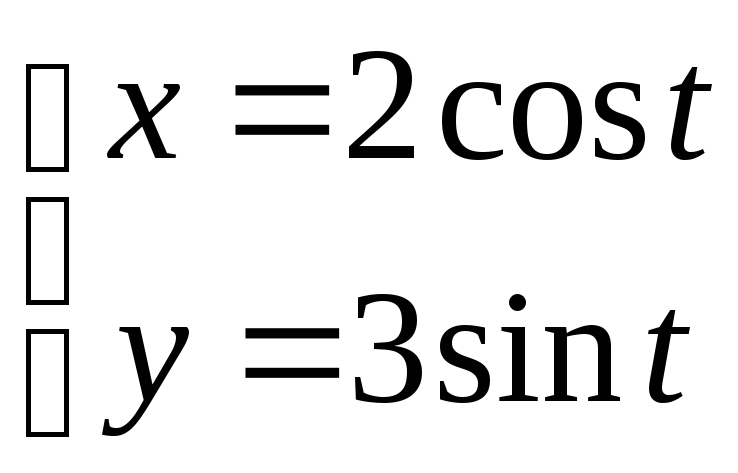
2)

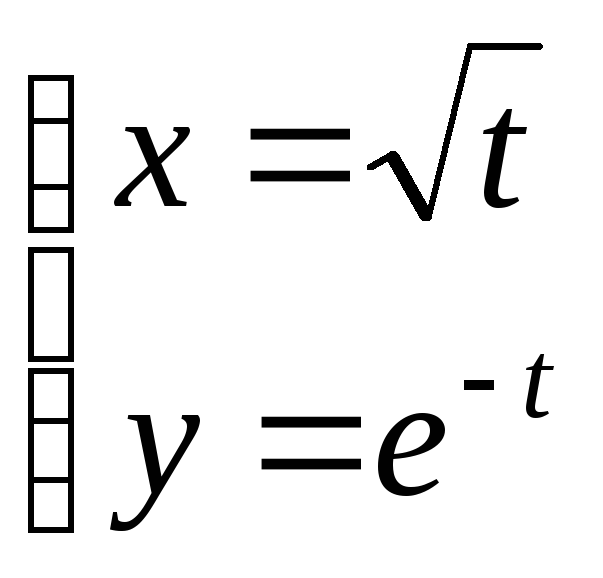
Решение:

1)

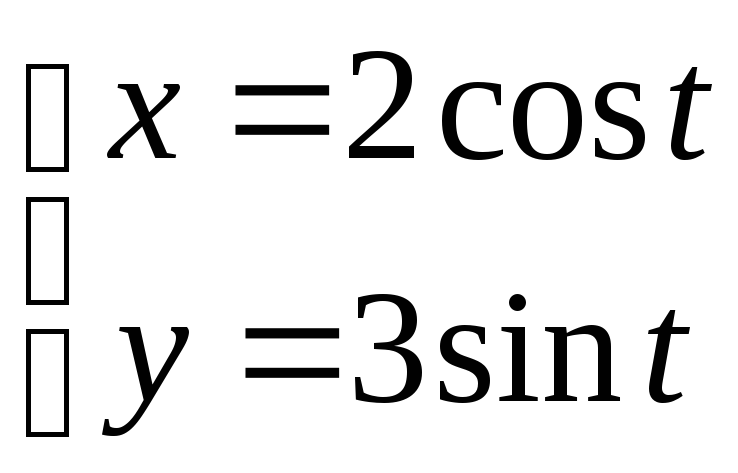
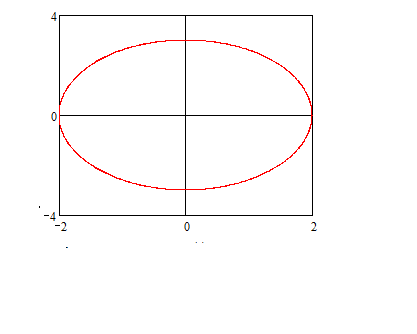
Исключим параметр T, для чего разделим обе части 1го уравнения на 2, 2го уравнения на 3, возведем их в квадрат и сложим

Получили каноническое уравнение эллписа с центром в точке О(0; 0), полуосями

2)

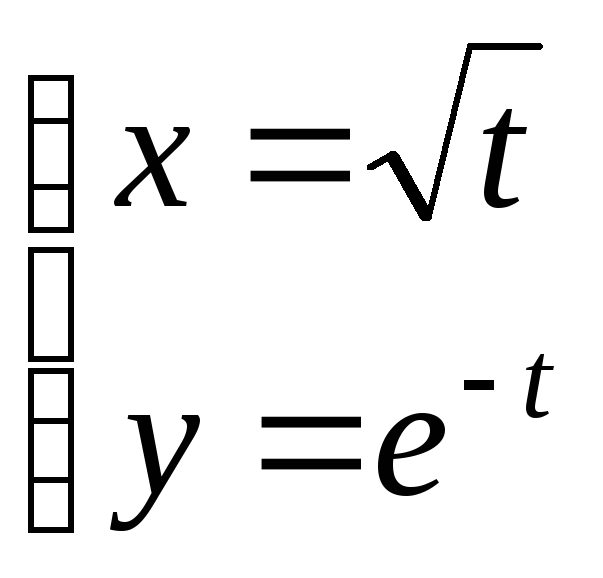
Исключим параметр t, для чего возведем первое уравнение в квадрат и подставим по 2е

Согласно 1му уравнению, область определения этой функции

Задача 6. Построить фигуры, заданные неравенствами

1)

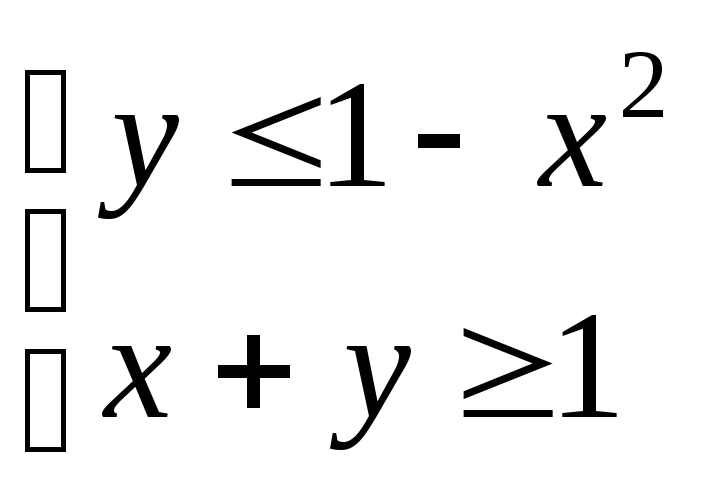
2)

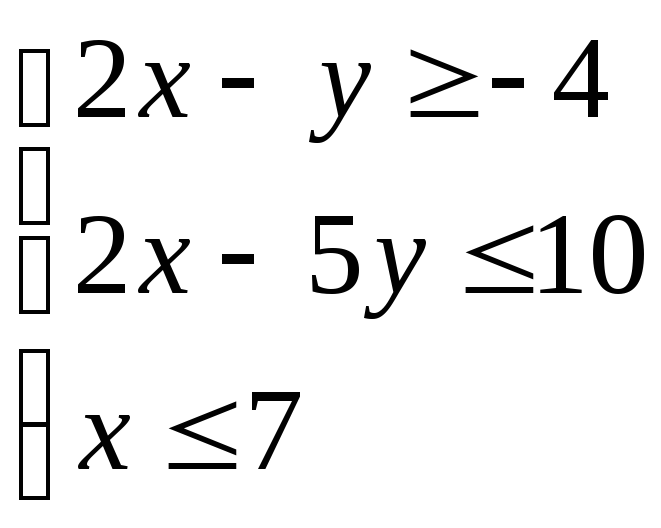
Решение:

1)

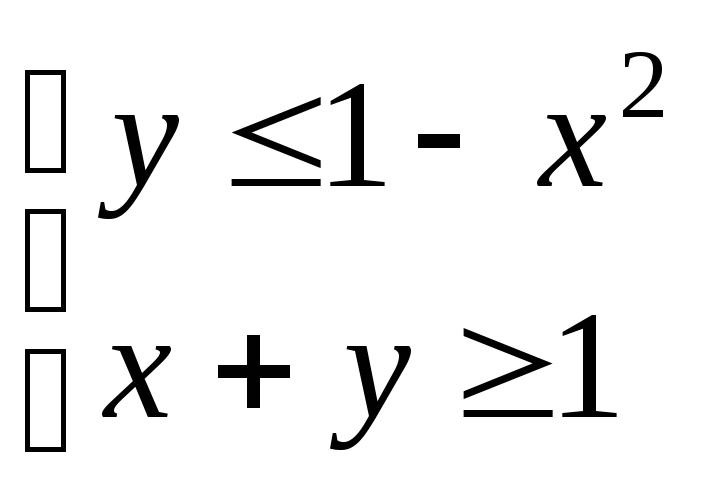
Строим границы области: параболу и прямую

Точки пересечения:

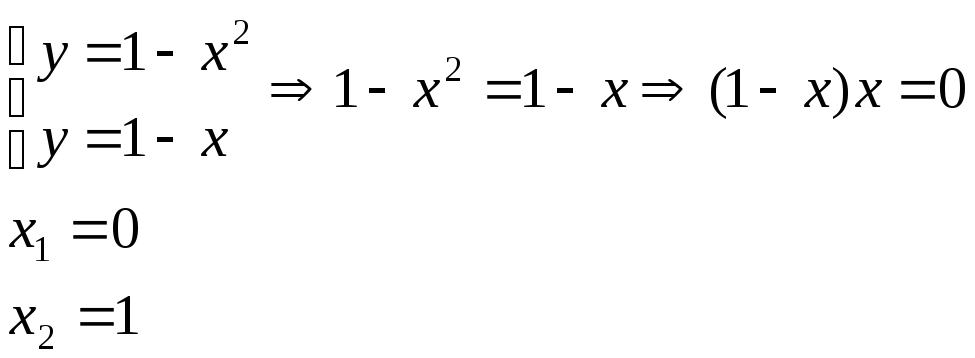
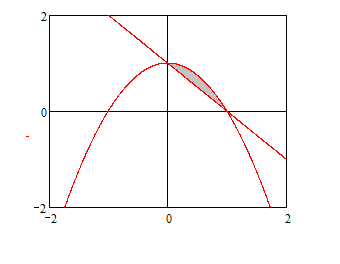
Искомая область расположена ниже параболы, т.к. , и выше прямой, т.к.

2)

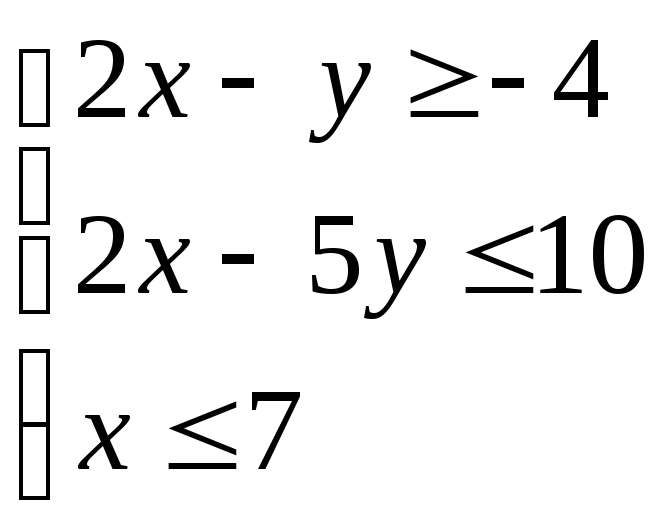
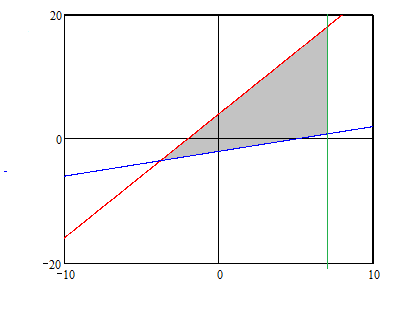
Строим 3 прямые, являющиеся границами области

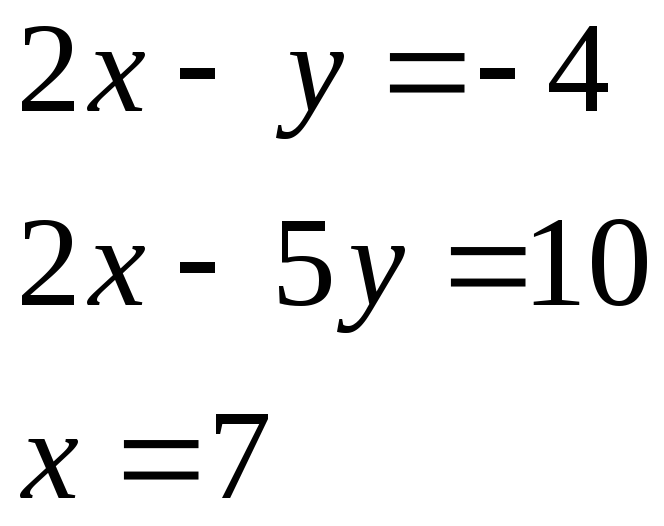
Найдем точки пересечения каждой из пар прямых

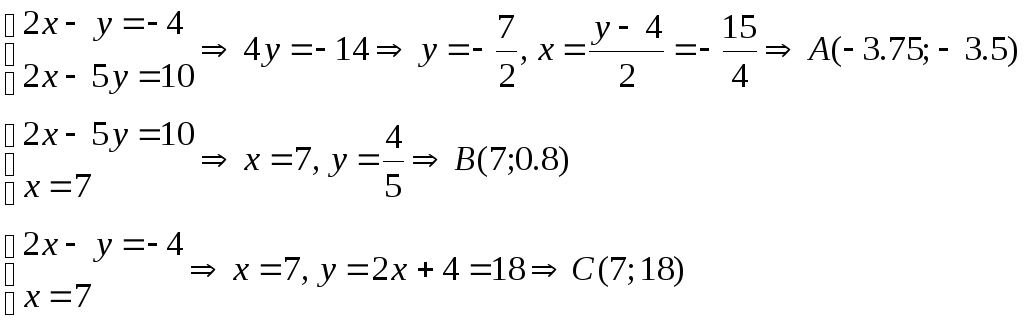
Искомая область лежит ниже первой прямой, выше второй прямой и левее третьей прямой.

16