Кузнецов_математика

Добавил:

Vezen Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Коломенский институт филиал МГМУ

Предмет:

Высшая математика

Файл:

15.13. ∑(−1)n

.pdf

Скачиваний:

416

Добавлен:

20.06.2014

Размер:

3 Мб

Скачать

☆

<<< < Предыдущая 3 4 5 6 7 8 9 10 11 12 13 1415 / 2715 16 17 18 19 20 21 22 23 24 25 26 27 > Следующая >>>

∞

12.7.

∑

x2n cos(x +π n).

n=1

4 3n

∞

12.9.

∑2n x3n sin

n=1

∞

12.11. ∑23n xn sin

n=1

∞

12.13. ∑3n xntg

n=1

∞

12.15. ∑x3ntg

n=1

∞

12.17. ∑16n x3narcsin

n=1

3 n

∞	2x
12.19. ∑2n xnarctg		.

n=1	n +1

∞	3x
12.21. ∑27n x3narctg		.

n=1	2n + 3

∞

12.23. ∑8n n2 sin3n x.

n=1

12.25. ∑∞ 3n tg2n x.

n=1 n

12.27. ∑∞ 4n sin2n x.

n=1 n2

12.29. ∑∞ 1 tgn x.

n=1 n2

∞			n 2
12.31. ∑	4	3		tgn (2x).

			n
n=1

∞

12.8. ∑

x2n sin(3x −π n).

n=1 2n

∞

12.10. ∑32n xn sin

n=1

∞

12.12. ∑3n x3n sin

n=1

∞

12.14. ∑8n x3ntg

n=1

4 n

∞

12.16. ∑

2n x3narcsin

n=1

∞

12.18. ∑32n x5narcsin

n=1

∞

12.20. ∑

2n x3narctg

2(n + 3)

n=1

∞

12.22. ∑

sin3n x.

n=1

∞

12.24. ∑

sin2n (2x).

n=1

∞

12.26. ∑

sinn

(3x).

n=1

∞

12.28. ∑

tgn (

2x).

n=1

∞

12.30. ∑

tgn x.

n 3n 2

n=1

Задача 13. Найти область сходимости функционального ряда.

∞				∞		n	(	x +1	n)
13.1. ∑2n2		e−n2	(x−1)3 .	13.2. ∑	ln					.
	x − 2

n=1				n=1				x − e

∞

2 n

−n

(

x+1

13.3. ∑ 1+

) .

n=1

∞

13.5.

∑e−(1−x n)

n=1

∞

13.7. ∑5−n

sin(x

+1)

n .

n=1

∞

13.9.

∑5nx arctg

7nx

(

x −1

n=1

)

∞

5 n

13.11. ∑ 1+

3−n

n=1

∞

+1)

13.13. ∑en

sin(x

n .

n=1

∞(ln(1+1n)+ lnln x)n

13.15.∑ .

n=1	x − e1 e
∞	1
13.17. ∑	1	.

	lnn (x +1 e)
n=1	lnn (x +1 e)
∞	n+1
∞	(−n1sin) x .
13.19. ∑	(−n1sin) x .
n=1	e

∞
13.21. ∑(−1)n 3−n2 ln(1+x n) .
n=1
∞						x
13.23. ∑n		x	arcsin			x	.
13.23. ∑n			arcsin				.
n=1					3nx
∞			2			2		+1)) .
13.25. ∑(−1)n−1 2−n						(lnn (x		+1)) .
n=1
∞	1
13.27. ∑	1			.
13.27. ∑	n			.
n=1	ln		x

∞

13.4. ∑n2

x −1

e−n x .

n=1

∞

1 n

(

x−1

13.6. ∑ 1+

) .

n=1

∞

13.8. ∑

lnn (x −1)

n=1

∞

13.10. ∑

lnn

(x +

n=1

∞

13.12. ∑

lnn

(x + e)

n=1

∞
13.14. ∑(−1)n+1 e−n cos x .
n=1
∞	n+1
	(−1)
13.16. ∑		.
	ln x
n=1	n

∞
13.18. ∑sinn xlnn .
n=1	x − n

13.20. ∑∞ (−1)n 5−n2 arctan(1(n x )) .

n=1

∞

cos

(n (x −1))

13.22. ∑

n=1

∞

13.24. ∑n2xarctg

n=1

2nx

∞

13.26. ∑nln

x −

en ln x .

n=1

∞

) .

13.28. ∑(−1)n 5−n(lnn

n=1

∞	−n4(sin1 n2x2 )				∞	(−1)n+1
13.29. ∑e			.		13.30. ∑	2	)	.
n=1					n=1 nln(1+x		)
∞		1	n	2
13.31. ∑	3+		4−n		x .
13.31. ∑	3+		4−n		x .
n=1		n

Задача 14. Найти область сходимости функционального ряда.

∞

(n − 2) (x + 3) .

14.1.

∑

n=1

2n + 3

∞

(x −1) .

14.3.

∑

n=1

n9n

∞

14.5.

∑(−1)n−1 (x − 2) .

n=1

∞

14.7.

∑

3n (x − 2)

n=1

∞

(x + 5)

2n−1

14.9.

∑

4n (2n −

n=1

∞

(x − 2)

14.11. ∑

(3n +1)2n

n=1

∞

14.13. ∑(x + 5)n tg

n=1

∞

14.15. ∑

n 9n (x

−1)

n=1

∞

(x + n2) .

14.17. ∑

n=1

∑∞ (3n − 2)(x − 3)n

14.19. .

n=1 (n +1)2 2n+1

	∞	(−1)n (x − 3)n
14.2.	∑	(		n +1 5n .
	n=1	(				)
	∞	2n + 3
14.4.	∑	2n + 3					.

				5		x2n
	n=1	(n +1)				x2n
	∞				2n+1
	∞	(x − 5) .
14.6.	∑	(x − 5) .
	n=1	3n +			8
	∞	n!
14.8.	∑	n!	.
14.8.	∑	n	.
	n=1	x

∞(x − 7)2n−1

14.10.∑n=1 (2n2 − 5n)4n .

∑∞ 3n(x − 2)3n .314.12.

n=2	(5n − 8)
∞
∞				n
14.14. ∑sin				n		(x − 2)n .
14.14. ∑sin						(x − 2)n .
n=1		n2		+1
∞
14.16. ∑3n2		xn2 .
n=1
∞	n		5
14.18. ∑	n				(x + 5)2n+1 .
14.18. ∑					(x + 5)2n+1 .
n=1	(n +1)!

∞(x − 5)n

14.20.∑n=1 (n + 4)ln(n + 4).

∞							1
14.21. ∑							1				.

	(n + 2)ln(n + 2)(x − 3)									2n
n=2	(n + 2)ln(n + 2)(x − 3)
∞	(x − 4)n2
14.23. ∑	n		n+1 .
n=1	n

∞		n +1
14.25. ∑		n +1				.
14.25. ∑	3n (x + 3)				n	.
n=5	3n (x + 3)
∞			3n + 5
14.27. ∑			3n + 5						.

	(2n + 9)			5	(x + 2)			2n
n=1	(2n + 9)				(x + 2)
∞	(x + 2)n
14.29. ∑							.
14.29. ∑	(2n +1)3n						.
n=1	(2n +1)3n
∞	(n +1)5 x2n
14.31. ∑	2n +1						.
n=1	2n +1

∞

14.22. ∑

2n n2 (x +

n=5

∞

14.24. ∑

n=1

∞

4n (x +1)2n

14.26. ∑

n=1

∞

14.28. ∑

5n (x + 4)

n=5

∞

n2 (x − 3)n

14.30. ∑

(

)

n=1

Задача 15. Доказать, исходя из определения, равномерную сходимость функционального ряда на отрезке [0,1]. При каких n абсолютная величина остаточного члена ряда не превосходит 0.1 x [0,1]?

∞

15.1. ∑(−1)n

15.2. ∑(−1)n

n=1

7n −11

n=1

5n −

∞

15.3. ∑(−1)n

15.4. ∑(−1)n

n=1

4n − 6

n=1

3 n3 − 5

∞

15.5. ∑(−1)n

15.6. ∑(−1)n

n=1

4n − 5

n=1

5n −

∞

15.7. ∑(−1)n

15.8. ∑(−1)n

n=1

3n − 4

n=1

3 n3 − 2

∞

15.9. ∑(−1)n

15.10. ∑(−1)n

n=1

6n −11

n=1

3 n3 − 7

∞

15.11. ∑(−1)n

15.12. ∑(−1)n

n=1

7n −10

n=1

6n − 8

∞

15.15. ∑(−1)n

n=1

∞

15.17. ∑(−1)n

n=1

∞

15.19. ∑(−1)n

n=1

∞

15.21. ∑(−1)n

n=1

∞

15.23. ∑(−1)n

n=1

∞

15.25. ∑(−1)n

n=1

∞

15.27. ∑(−1)n

n=1

∞

15.29. ∑(−1)n

n=1

∞

15.31. ∑(−1)n

n=1

8n −12

5n − 8.

4n − 7 .

7n −13

3n − 5.

8n −11.

3 8n3 −12

9n −15

3 n3 − 6

∞

15.14. ∑(−1)n

n=1

∞

15.16. ∑(−1)n

n=1

∞

15.18. ∑(−1)n

n=1

∞

15.20. ∑(−1)n

n=1

∞

15.22. ∑(−1)n

n=1

∞

15.24. ∑(−1)n

n=1

∞

15.26. ∑(−1)n

n=1

∞

15.28. ∑(−1)n

n=1

2n − 3.

6n − 7 .

6n −10

5n − 7 .

3 8n3 − 21

3 8n3 −19

3 8n3 −11

3 n3 − 3

∞	x	n
15.30. ∑(−1)n	x		.
15.30. ∑(−1)n	10n −12		.
n=1	10n −12

Задача 16. Для данного функционального ряда построить мажорирующий ряд и доказать равномерную сходимость на указанном отрезке.

∑∞ xn

16.3. n=1 nn , [−2, 2].

	∞	n
16.2.	∑	x	,	[−		3		,		3	].
16.2.	∑	n	,	[−				,	2		].
	n=1	n2			2				2
	∞	n		x	n							3		3
16.4.	∑						,		[−				,		].
16.4.	∑						,		[−				,		].
	n=1	n +1 2										2	2
	∞	(x − 3)n					[−1, 6].
16.6.	∑	n5		n	,		[−1, 6].
	n=1	n5

(x −1)n

∞(x − 3)n

16.7.∑(−1)n (2n +1) n +1, [2, 4].n=0

∞

16.9. ∑(x −1)

[−1, 3].

n=1

n9n

(x − 2)

∞

16.11. ∑(−1)

[1, 3].

+1)

ln(n

+1)

n=1

∞

n−1

2n−1

16.13. ∑

[−

(4n − 3)

n=1

∞

2n−1

(x +25)n

16.15. ∑

[−7,

− 3].

n=1

∞

(−1)

n−1

16.17. ∑

[−

n=1

∞

n−1 (x − 2)

16.19. ∑(−1)

[

n=1

∞

(x − 2)

16.21. ∑

[1, 3].

(2n −1)2n

n=1

∞

16.23. ∑

[−1, 1].

n(n + 2)

n=1

∞

16.25. ∑

[−2, 2].

n=0 3

∞

16.27. ∑n=0 2n (n + 3), [0, 2].

∞	n(x + 2)	n

16.29. ∑(−1)n−1			, [−3, −1].

n=0	(n +1)3 n + 2

∞(x +1)n

16.31.∑n=1 (n +1)ln2 (n +1), [−2, 0].

∞

x)cos

16.8. ∑(π −

nx,

[0,

π ].

n=0

4 n7 +1

∞

n!(x + 3)

16.10. ∑

[−5, -1].

n=1

∞

16.12. ∑

, [−3, 3].

n=1

∞

n−1

16.14. ∑

[−2, 2].

n=1

n3 lnn

∞

(x + n2)

16.16. ∑

[−3, -1].

n=1

∞

(n +1)

16.18. ∑

, [−

2n +1

n=0

∞

(x +25)

16.20. ∑

[−6,

− 4].

n=1

∞

(x +1)sin

nx,

16.22. ∑

[−3, 0].

n n +1

n=1

∞(x + 5)n

16.24.∑ 3n +1 n2 +1, [−6, − 4].n=0

∞		π				n
16.26. ∑ sin					(x − 2)		, [1, 3].
16.26. ∑ sin			n		(x − 2)		, [1, 3].
n=0		2
∞	(x +1)			2n
∞
16.28. ∑					, [−1, 0].
n=1	n4n

∞(x − 3)2n

16.30.∑ n n +1 , [2, 4].n=0

(−1)n+1

Задача 17. Найти сумму ряда.

∞	n−1				1
17.1. ∑(−1)
		1	+				xn−1 .

n=1					n
∞	n+1	1					1
17.3. ∑(−1)
				−				xn+2 .
						n + 2
n=1		n

∞ 1+ (−1)n

17.5. ∑ x2n+1 . n=0 2n +1

∞(−1)n−1 xn

17.7.∑n=2 n(n −1) .

∞	x	n
17.9. ∑	x			.
17.9. ∑				.
n=1 n(n +1)
∞			x	2n+2
17.11. ∑			x						.

	(2n +1)(2n + 2)
n=0	(2n +1)(2n + 2)
∞			n−1		x		n+1
17.13. ∑(−1)			n−1		x			.

				n	(	n +1
n=1					(		)

∞x2n−1

17.15.∑n=1 2n(2n −1).

∞

(−1)n+1

17.17. ∑

xn−1 .

n=1

∞

(−1)

n+1

17.19. ∑

(n +1)(n +

n=0

∞

2n+1

17.21. ∑

2n(2n +1)

n=1

∞

n+2

17.23. ∑

(n +1)(n +

n=0

∞

17.2.

∑

(2n − 3)(2n − 2)

n=2

∞

(−1)

n−1

2n−1

17.4.

∑

n=1

4n (2n −1)

∞

n−1

17.6. ∑(−1)

−

n=1

n x

∞

n−1

17.8.

∑

1+ (−1)

x2n+1 .

n=0

2n +1

∞(−1)n−1 x2n+2

17.10.∑n=0 16n (2n +1) .

∞	n−1		1		1
17.12. ∑(−1)				+
						xn .

n=1		n			n +1

∞e−nx

17.14.∑n=1 n .

∞	n		1
17.16. ∑ (−1)		+		x2n .
17.16. ∑ (−1)		+		x2n .
n=1			n

∞

17.18. ∑n=1 n(n +1)xn+1 .

∞	sin			n	x
17.20. ∑	sin				x	.
17.20. ∑	n(n −1)					.
n=2	n(n −1)
∞		1			1
17.22. ∑			+				xn .
17.22. ∑			+				xn .
n=1	n				n +1
∞					(−1)n
17.24. ∑	2n +				n		xn .
n=1					n

∞x2n

17.25.∑n=2 (2n − 2)(2n −1).

∞(−1)n+1 cosn+1 x

17.27.∑ .

n=1	n(n +1)
∞	n
17.29. ∑	3	.
17.29. ∑	(n +1)xn+1	.
n=0	(n +1)xn+1

∞x2n+2

17.31.∑n=0 (2n + 2)(2n + 3).

Задача 18. Найти сумму ряда.

∞

18.1. ∑(4n2 + 9n + 5)xn+1 .

n=0

∞

18.3. ∑(n2 + n +1)xn+3 .

n=0

∞

18.5. ∑(n2 + 5n + 3)xn .

n=0

∞

18.7. ∑(3n2 + 8n + 5)xn+2 .

n=0

∞

18.9. ∑(2n2 + 7n + 5)xn+1 .

n=0

∞

18.11. ∑n(2n −1)xn+2 .

n=0

∞

18.13. ∑(2n2 − n −1)xn .

n=0

∞

18.15. ∑(n2 + 7n + 4)xn .

n=0

∞

18.17. ∑(2n2 + 2n +1)xn .

n=0

∞	x	n
17.26. ∑	x		.
17.26. ∑	n(n −1)		.
n=2	n(n −1)
∞	(−1)n+1 tgn x
17.28. ∑	n(n +1)			.
n=1	n(n +1)

∞n + (−1)n

17.30.∑n=2 n(n −1) xn .

∞

18.2. ∑(3n2 + 7n + 4)xn .

n=0

∞

18.4. ∑(2n2 + 4n + 3)xn+2 .

n=0

∞

18.6. ∑(2n2 + 5n + 3)xn+1 .

n=0

∞

18.8. ∑(2n2 + 8n + 5)xn .

n=0

∞

18.10. ∑(3n2 + 7n + 5)xn .

n=0

∞

18.12. ∑(n2 − n +1)xn .

n=0

∞

18.14. ∑(3n2 + 5n + 4)xn+1 .

n=0

∞

18.16. ∑(2n2 − n − 2)xn+1 .

n=0

∞

18.18. ∑(n2 + 2n −1)xn+1 .

n=0

∞

18.19. ∑(n2 + 2n + 2)xn+2 .

n=0

∞

19.21. ∑(n2 + 5n + 4)xn+2 .

n=0

∞

18.23. ∑(n2 − 2n −1)xn+1 .

n=0

∞

18.25. ∑(n2 − 2n − 2)xn+1 .

n=0

∞

18.27. ∑(n2 + 6n + 5)xn+1 .

n=0

∞

18.29. ∑(2n2 + n +1)xn+1 .

n=0

∞

18.31. ∑(n2 + 9n + 5)xn+1 .

n=0

∞

18.20. ∑(n2 + 4n + 3)xn+1 .

n=0

∞

18.22. ∑(2n2 − 2n +1)xn .

n=0

∞

18.24. ∑(n2 − 2n + 2)xn .

n=0

∞

18.26. ∑(4n2 + 6n + 5)xn .

n=0

∞

18.28. ∑n(2n +1)xn+2 .

n=0

∞

18.30. ∑(2n2 + n −1)xn .

n=0

Задача 19. Разложить функцию в ряд Тейлора по степеням x.

19.1. 20 − x − x2 .

19.3. ln(1− x − 6x2 ).

19.5. sh2x − 2. x

19.7..

3 27 − 2x

19.9. (x −1)sin5x.

19.11. 8+ 2x − x2 .

19.13. ln(1− x −12x2 ).

19.15. arcsinx −1. x

19.2..

− 5x4

19.4. 2xcos2 (x2)− x.

19.6. 12 + x − x2 .

	(							)
19.8.	ln 1+ x − 6x2								.
		ch3x −1
19.10.					.
19.10.			x2		.
			x2
19.12.	1					.


		4 16 −
		4 16 −		3x
19.14. (3+ e−x )2 .
19.16.	7						.

		12 − x − x2

19.17. x2 4 − 3x .

19.19. 2xsin2 (x2)− x.

19.21. 6 + x − x2 .

19.23. ln(1+ x −12x2 ).

arctgx

19.25..

19.27. 416 − 5x .

19.29. (2 − ex )2 .

19.18. ln(1+ 2x − 8x2 ). 19.20. (x −1)shx.

19.22. x327 − 2x .

19.24. sin3x − cos3x. x

19.26. 6 − x − x2 .

19.28. ln(1− x − 20x2 ).

19.30. (x −1)chx.

19.31. 2 − x − x2 .

Задача 20. Вычислить интеграл с точностью до 0,001.

0,1

20.1. ∫e−6x2 dx.

20.3. ∫cos x2dx.

20.2. 0,1∫sin(100x2 )dx.

0,5 dx

20.4. ∫0 4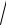1+ x4 .

0,11− e−2x

20.5. ∫ x dx.

1,5 dx

20.7. ∫0 3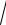27 + x3 . 20.9. 0,2∫ sin(25x2 )dx.

1dx

20.11.∫0 4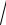16 + x4 .

0,4 ln(1+ x 2)

20.13. ∫ dx.

0 x

	1	ln(1	+ x 5)
20.6.	∫	ln(1	+ x 5)	dx.
20.6.	∫			dx.
	0		x
	0
	0,2
20.8.	∫ e−3x2 dx.
	0

20.10. 0,5∫ cos(4x2 )dx.

0,2 1− e−x

20.12. ∫ dx.

0 x

2dx

20.14.∫0 3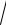64 + x3 .

<<< < Предыдущая 3 4 5 6 7 8 9 10 11 12 13 1415 / 2715 16 17 18 19 20 21 22 23 24 25 26 27 > Следующая >>>

Соседние файлы в предмете Высшая математика

#
20.06.2014381 Кб81Доказательства по линейной алгебре.docx
#
20.06.20143 Мб416Кузнецов_математика.pdf
#
20.06.2014952 Кб534Ответы на вопросы к экзамену по математике (шпаргалки).doc
#
20.06.20142 Мб189ТПУ Линейная алгебра 1курс ИДЗ №1.doc
#
20.06.2014380 Кб66ТПУ Линейная алгебра 1курс ИДЗ №2.doc
#
20.06.2014539 Кб61ТПУ Линейная алгебра 1курс ИДЗ №3.doc
#
20.06.20141 Мб67ТПУ Линейная алгебра 1курс ИДЗ №4.doc