Кузнецов_математика

Добавил:

Vezen Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Коломенский институт филиал МГМУ

Предмет:

Высшая математика

Файл:

17.1. y = xeax .

17.2. y = sin2x + cos(x +1).

17.3. y = 5 e7x−1 .

.pdf

Скачиваний:

408

Добавлен:

20.06.2014

Размер:

2.87 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 276 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

x = arcsin

15.19.

y = 1+

t .

x = t

t2 +1,

15.21.

1+ t

y = ln

(1− t

x = ln

15.23.

y = arcsin

1− t2 .

x = ln 1− sint ,

1+ sint

y = 1 tg2 t + lncost.

x = lntgt,
	1
15.27.
y =				.
	sin	2
			t

	sec2 t	,
x = e		,
15.29.

y = tgt lncost + tgt − t.

x = ln(t + 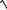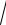1+ t2 ),

15.31.

y = 1+ t2 − ln1+ 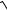1+ t2 .t

x =

(arcsint)2 ,

15.20.

y =

1− t2

x = arctgt,

15.22.

1+ t

y = ln

t +1

x = arctg

−

15.24.

1− t

y = arcsin

1−t

x =

t − t2

− arctg

15.26.

t −

1− t arcsin

y =

lnt

x =

+ ln 1−t2 ,

1− t

15.58.

y =

arcsint + ln

1− t2 .

1− t

x =

arcsint + ln

1−t2 ,

1−t

15.30.

y =

1− t

Задача 16. Составить уравнения касательной и нормали к кривой в точке,

соответствующей значению параметра t = t0 .

x = asin3 t,
x = asin3 t,					3cost,
				x =	3cost,
16.1.			= π 3.	16.2.				= π 3.
y = acos3 t,	t	0	= π 3.	y = sint,		t	0	= π 3.
		0					0

x = a(t − sint),

16.3.

y = a(1− cost),

=π 3.

2t + t3

x =

1+ t

16.5.

2t − t2

y =

=1.

1+ t

x = t(tcost − 2sint),

16.7.

y = t(tsint + 2cost),

=π 4.

x = 2ln	(ctgt)+ ctgt,
16.9.		t0 =π 4.
y = tgt	+ ctgt,	t0 =π 4.
x = atcost,
16.11.
y = atsint, t0		= π 2.

								t
x = arcsin													,

						1+ t				2
						1+ t
16.13.								1
y = arccos								1						,
y = arccos														,
							1+ t				2
							1+ t
	1+ t
x =			,
x =	t2		,
16.15.	3			2
y =	3		+	2		,		t				= 2.
y =			+			,		t				= 2.
	2t	2			t				0
	2t				t

x = a(tsint + cost),

16.17.

y = a(sint − tcost),

	−t		,
x =1	−t	2	,
		2
16.19.	− t3, t				= 2.
y = t	− t3, t			0	= 2.
				0

t0 =1.

t0 =π4.

									2
x = 2t −t												,
16.4.																						=1.
y = 3t −t3,																	t		0			=1.
																			0
																		t
x = arcsin																												,

															1+ t									2
															1+ t
16.6.																				1
y = arccos																				1									,	t = −1.
y = arccos																													,	t = −1.
																1+ t									2						0
																1+ t
		3at
x =											,
x =	1+ t							2			,
	1+ t
16.8.	3at2
y =	3at2										,					t						= 2.
y =											,					t						= 2.
	1+ t							2										0
	1+ t
		1				2								1							4
x =					t					−							t					,
x =			2		t					−				4			t					,
16.10.		1												1 3
		1					2							1 3
y =					t +												t , t0 = 0.
		2												3
x = sint,
16.12.
y = cost,																t0						= π 6.
		1+ lnt
x =															,
x =					t2										,
16.14.				3+ 2lnt
				3+ 2lnt

y =									t											,					t0					=1.
									t
											3
x = asin											3		t,
x = asin													t,
16.16.																											= π 6.
y = acos3 t,																						t	0				= π 6.
																							0
			t +1
x =											,
x =					t						,
16.18.				t −1
				t −1

y =					t						,					t0						= −1.
					t
																		),
x = ln(1+ t																2		),
																2
16.20.
y = t − arctgt,																										t			0	=1.
																													0

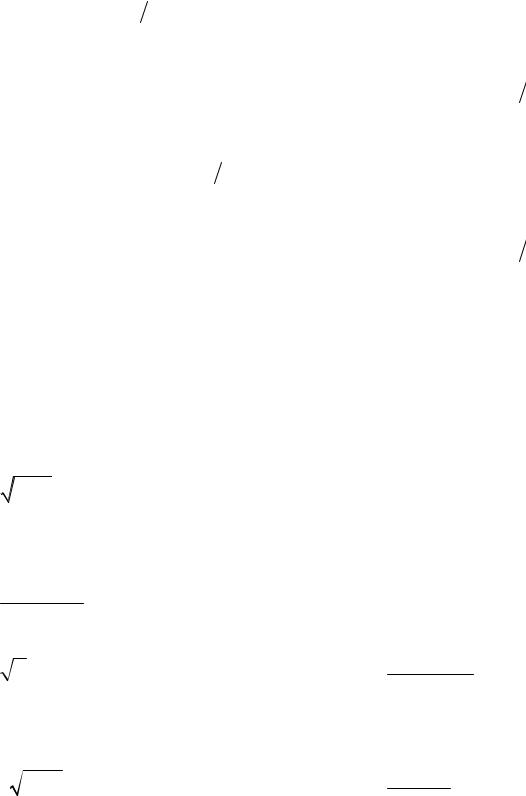
x = t	(1− sint),
16.21.
y = tcost						,		t0	= 0.
x = 3cost,
16.23.
y = 4sint,								t0	= π 4.
	3
x = t		+1,
16.25.		+ t				+1,					=1.
y = t2		+ t				+1,			t	0	=1.
										0
x = 2tgt,
16.27.								+ sin2t, t0 = π 4.
y = 2sin					2 t			+ sin2t, t0 = π 4.
x = sint,
16.29.
y = at ,					t0			= 0.
			t
x = 2e			t	,
x = 2e				,
16.31.								= 0.
y = e−t ,						t	0	= 0.
							0

12+ t

x =

−1

16.22.

y =

= 2.

−1

− t

x = t

16.24.

2 − t3, t

=1.

y = t

x = 2cost,

16.26.

t0 = −π 3.

y = sint,

x = t

+1,

16.28.

= −2.

y = t

2 ,

x = sint,

16.30.

y = cos2t,

= π 6.

Задача 17. Найти производную n-го порядка.

17.5. y = lg(5x + 2).

17.7. y = 2(3x + 2).

17.9. y = 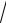x.

17.11. y = 23x+5.

17.13. y = 3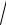e2x+1 .

17.15. y = lg(3x +1).

17.6. y = a3x.

17.8. y = lg(x + 4).

17.10. y = 2x + 5 . 13(3x +1)

17.12. y = sin(x +1)+ cos2x.

17.14. y = 4 +15x. 5x +1

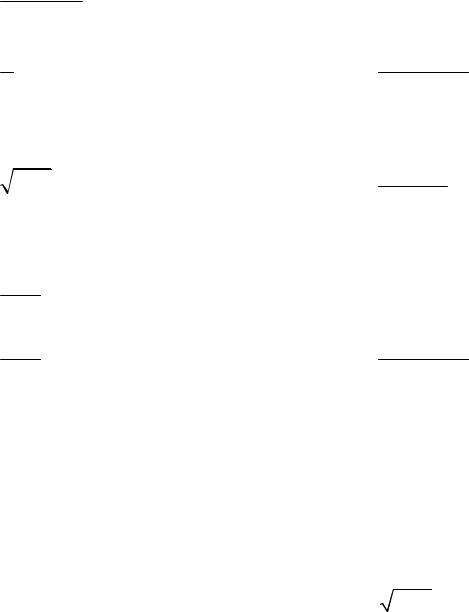
17.16. y = 75x.

17.17. y = 9(4x + 9).

17.19. y = 4. x

17.21. y = a2x+3.

17.23. y = 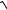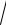e3x+1 .

17.25. y = lg(2x + 7).

17.27. y = x +1.

1+ x

17.29. y = 1− x.

17.31. y = 32x+5.

17.18. y = lg(1+ x).

17.20. y = 5x +1 . 13(2x + 3)

17.22. y = sin(3x +1)+ cos5x.

17.24. y = 11+12x. 6x + 5

17.26. y = 2kx.

17.28. y = log3 (x + 5).

17.30. y = 7x +1 . 17(4x + 3)

Задача 18. Найти производную указанного порядка.

18.1. y =

(

2x2 − 7

)

(

)

= ?

18.2. y =

(

3− x2

)

= ?

x −1 ,

ln2 x,

yIII

18.3. y = xcos x2 ,

yIII = ?

18.4. y =

ln(x −1)

yIII = ?

x −1

18.5. y =

log2 x

yIII = ?

18.6. y = (

4x3 + 5)e2x+1,

= ?

18.7. y = x2 sin(5x − 3),

yIII

= ?

18.8. y =

ln x

yIV = ?

(

)

18.9. y =

2x + 3

yIII = ?

18.10. y =

(

yIII = ?

ln2 x,

1+ x2

arctg x,

18.11. y =

ln x

yIV

= ?

18.12. y = (4x + 3) 2− x ,

= ?

18.13. y = e1−2x sin(2 + 3x),

yIV

= ?

18.14. y =

ln(3+ x)

yIII

= ?

(

)

(

3+ x

(

)

18.15. y =

= ?

18.16. y =

x2 +

)

x − 3

yIV = ?

2x3

+1 cos x,

18.17. y = (1− x − x2 )e(x−1) 2 ,

yIV = ?

18.18. y =

sin2x,

yIII = ?

18.19. y = (x + 7)ln(x + 4),

= ?

18.20. y = (3x − 7) 3− x ,

yIV

= ?

18.21. y =

ln(2x + 5)

, yIII = ?

18.22. y = ex 2 sin2x,

yIV = ?

2x + 5

18.23. y =

ln x

, yIII

= ?

18.24. y = xln(1− 3x),

yIV

= ?

(

)

(

)

+2 ,

2−x ,

18.25. y =

x2 + 3x +1 e3x

= ?

18.26. y =

5x − 8

yIV

= ?

18.27. y =

ln(x − 2)

= ?

18.28.

x − 2

y = e− x (cos2x − 3sin2x),

yIV

= ?

18.29. y = (

5x −1)ln2 x,

yIII

= ?

18.30. y =

log3 x

yIV = ?

18.31. y = (x3 + 3)e4x+3,

yIV

= ?

Задача 19. Найти

производную

второго порядка y′′

от

функции, заданной

параметрически.

x = cos2t,

19.1.

y = 2sec2 t.

		t
x = e		t	cost,
x = e			cost,
19.3.	y = et sint.
	y = et sint.

x = t + sint,
19.5.
y = 2			− cost.

			t,
x =			t,
19.7.
y =1				1− t .

x = tgt,

19.9.

y =1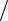sin2t.


		1			− t		2	,
x =		1			− t			,
19.2.
y =1 t.

				2
x = sh				2		t,
x = sh						t,
19.4.	y =1 ch2 t.
	y =1 ch2 t.

x =1 t,

19.6.			(1+ t					2	).
y =1			(1+ t						).

x = sint,
19.8.
y = sect.

					t −1,
x =					t −1,
19.10.
y = t						1− t .


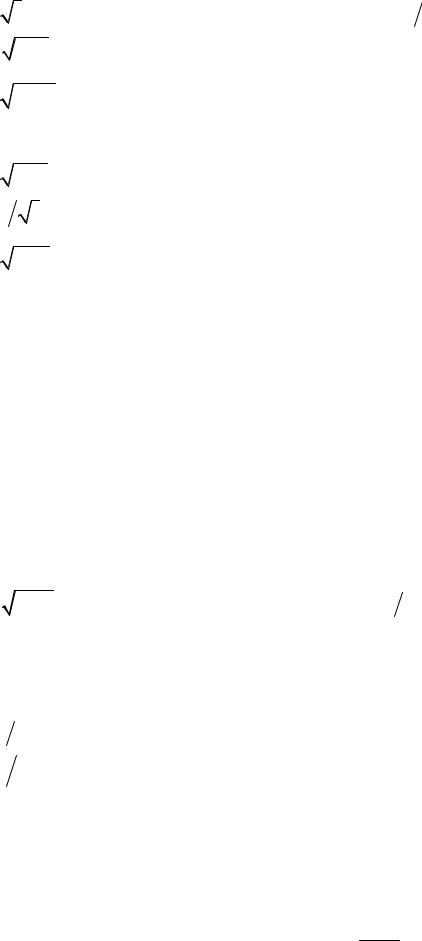
		t,
x =		t,
19.11.
y = 3		t −1.


		t	3	−1,
x =		t		−1,
19.13.
y = lnt.


		t −1,
x =		t −1,
19.15.
y =1				t .


		t − 3,
x =		t − 3,
19.17.	y = ln(t − 2).



x = t + sint,
19.19.
y = 2		+ cost.

x = cost,
19.21.
y = lnsint.
		t

19.23. x = e ,
y = arcsint.
x = cht,

19.25.
19.25.
y = 3				sh2 t.

x = 2			(t − sint),

19.27.	y = 4		(		2 + cost).
	y = 4		(		2 + cost).

					2
					,
x =1 t					,
19.29.				(t2 +1).
y =1				(t2 +1).

x = lnt,

y = arctgt.

Задача 20. Показать, что функция

y= xe−x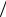22 ,

20.1.xy′ = (1− x2 )y. (1)

x = cost (1+ 2cost),

19.12.

y = sint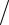(1+ 2cost).

x = sht,

19.14.

y = th2 t.

x = cos2 t,

19.16.

y = tg2 t.

x = sint,

19.18.

y = lncost.

x = t − sint,

19.20.

y = 2 − cost.

x = cost + tsint,

19.22.

y = sint − tcost.

x = cost,

19.24.

y = sin4 (t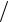2).

x = arctgt,

y = t2 2.

x = sint −tcost,

y = cost + tsint.19.28.

x = cost + sint,

y = sin2t.

y удовлетворяет уравнению (1).

y = sin x ,

20.2.x

xy′ + y = cos x. (1)

y= 5e−2x + ex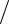3,

20.3.y′ + 2y = ex . (1)

y= x 1− x2 ,

20.5.

yy′ = x − 2x3. (1)

y = −	1		,

20.7.	3x + c
y′ = 3y2.		(1)

y= 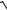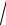x2 − cx,

20.9.(x2 + y2 )dx − 2xydy = 0. (1)

20.11.	y = etg(x 2),
20.11.	y′sin x = yln y.								(1)
	y =	b + x				,
20.13.	1+ bx					,
	y − xy′ = b(1+ x2 y′). (1)

								x 2
	y = ln				1+ e				+1,
	y = ln								+1,
20.15.						2
	(1+ ex )yy′ = ex .								(1)

	y = −		2				−1,
20.17.	y = −		x2				−1,
20.17.			x2
	1+ y2 + xyy′ = 0.								(1)
	y = a +				7x			,
20.19.	y = a +			ax +1				,
20.19.				ax +1

y− xy′ = a(1+ x2 y′). (1)

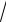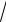y= 4x + x +1,

20.21.		−1
8xy′ − y =		−1		. (1)
8xy′ − y =				. (1)
	y3		x +1

y= 2 + c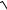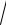1− x2 ,

20.4.(1− x2 )y′ + xy = 2x. (1)

y= c ,

20.6.cos x

y′ − tg x y = 0. (1)

y = ln(c + ex ),

20.8.

y′ = ex−y . (1)

y = x(c − ln x),

20.10. (x − y)dx + xdy = 0. (1)

20.12.

y = 1+ x , 1− x

y′ = 1+ y2 . (1) 1+ x2

y= 3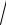2 + 3x − 3x2 ,

20.14.yy′ = 1− 2x. (1) y

y= tgln3x,

20.16. (1+ y2 )dx = xdy. (1)

20.18.

y = 3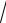x − ln x −1,

ln x + y3 − 3xy2 y′ = 0. (1)

y= atg 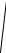a −1,

20.20. x

a2 + y2 + 2x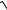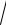ax − x2 y′ = 0. (1)

y = (x +1)ex2 ,

20.22.

y′ − 2xy = 2xex2 . (1)

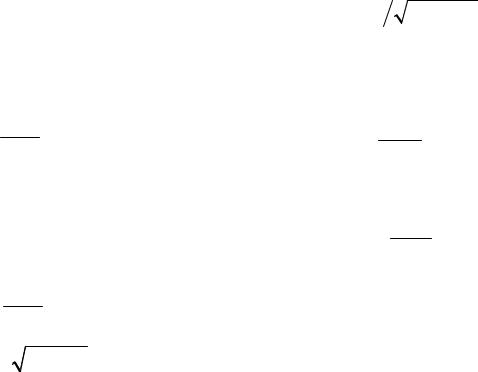
	2x	1
y =		+		,			y = ex+x2 + 2ex ,
y =	x3 +1	+	x	,			y = ex+x2 + 2ex ,
20.23.					x3 − 2		20.24.
x(x3 +1)y′ + (2x3 −1)y =					x3 − 2	. (1)	y′ − y = 2xex+x2	. (1)
x(x3 +1)y′ + (2x3 −1)y =						. (1)	y′ − y = 2xex+x2	. (1)
					x

y = −xcos x + 3x,							y =1 sin x + x ,
y = −xcos x + 3x,							20.26. 2sin x y′ + ycos x =
20.25.							20.26. 2sin x y′ + ycos x =
xy′ = y + x2 sin x. (1)							= y3 (xcos x − sin x). (1)
							= y3 (xcos x − sin x). (1)

20.27.x −1 +

x(x −1)y′ + y = x2 (2x −1). (1)x2 ,y =

y= (x +1)n (ex −1),

20.29.ny

y′ − x +1 = ex (1+ x)n . (1)

y= − x4 − x2 ,

20.31.

xyy′ − y2 = x4. (1)

y = x ,

20.28.cos x

y′ − ytg x = sec x. (1)

y = 2sin x + cos x, x

20.30.xsin x y′ + (sin x − xcos x) y =

=sin x cos x − x. (1)

III. ГРАФИКИ

Теоретические вопросы

1.Условия возрастания функции на отрезке.

2.Условия убывания функции на отрезке.

3.Точки экстремума. Необходимое условие экстремума.

4.Достаточные признаки максимума и минимума функции (изменение знака первой производной).

5.Наибольшее и наименьшее значения, функции, непрерывной на отрезке.

6.Выпуклость и вогнутость графика функции. Достаточные условия выпуклости и вогнутости.

7.Точки перегиба графика функции. Необходимое условие перегиба. Достаточные условия перегиба.

8.Исследование функций на экстремум с помощью высших производных.

9.Асимптоты графика функции.

		Теоретические упражнения
	1. Доказать, что функция		f (x) = x − sin x монотонно возрастает на отрезке: а)
[0,	2π ];	б) [0, 4π ] Следует ли из		монотонности		дифференцируемой функции
монотонность ее производной?
	2. Доказать теорему: если функции ϕ (x)				и ψ (x)	дифференцируемы на отрезке
[a,	b]	и ϕ′(x) >ψ ′(x)	x (a,	b),	а ϕ (a) =ψ (a), то ϕ (x) >ψ (x)
x (a,		b].

Дать геометрическую интерпретацию теоремы.

У к а з а н и е. При доказательстве теоремы установить и использовать монотонность функции

f(x) = ϕ (x) −ψ (x).

3.Доказать неравенство 2x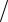π < sin x для трех случаев:

					2
а) x	0,	arccos				;

					π
			2		π
б) x arccos				,		;
			π
					2

	0,	π
в) x	0,	.
		2

Дать геометрическую интерпретацию неравенства.

4. Исходя из определений минимума и максимума, доказать, что функция

	−1 x		2
f (x) = e			, x ≠ 0,
	0,		x = 0

имеет в точке x = 0 минимум, а функция
		−1 x2
f (x) = xe			, x ≠ 0,
	0,		x = 0

не имеет в точке x = 0 экстремума.
5. Исследовать на экстремум в точке	x		функцию f (x) = (x − x	)n ϕ (x), считая,
		0	0

что производная ϕ′(x) не существует, но функция ϕ (x) непрерывна в точке x и
	0
ϕ (x0 ) ≠ 0, n.— натуральное число.
6. Исследовать знаки максимума и минимума функции x3 − 3x + q	и выяснить
условия, при которых уравнение x3 − 3x + q = 0 имеет а) три	различных

действительных корня; б) один действительный корень.

7. Определить «отклонение от нуля» многочлена p(x) = 6x3 − 27x2 + 36x −14 на отрезке [0, 3], т. е. найти на этом отрезке наибольшее значение функции p(x) .

8. Установить условия существования асимптот у графика рациональной функции.

Расчетные задания

Задача 1. Построить графики функций с помощью производной первого порядка.

1.1. y = 2x3

− 9x2 +12x − 9.

1.2. y = 3x − x3.

1.3. y = x2 (x − 2)2 .

1.4. y = (x3 − 9x2 )

4 + 6x − 9.

1.5. y = 2 − 3x2 − x3.

1.6. y = (x +1)2 (x −1)2 .

1.7. y = 2x3

− 3x2 − 4.

1.8. y = 3x2 − 2 − x3.

(

)

(

)

(

)

1.9. y =

x −1 2

x − 3

2 .

1.10. y =

x3 + 3x2

4 − 5.

<<< < Предыдущая 1 2 3 4 56 / 276 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете Высшая математика

#
20.06.2014380.9 Кб75Доказательства по линейной алгебре.docx
#
20.06.20142.87 Mб408Кузнецов_математика.pdf
#
20.06.2014951.81 Кб526Ответы на вопросы к экзамену по математике (шпаргалки).doc
#
20.06.20142.31 Mб175ТПУ Линейная алгебра 1курс ИДЗ №1.doc
#
20.06.2014380.42 Кб63ТПУ Линейная алгебра 1курс ИДЗ №2.doc
#
20.06.2014539.14 Кб56ТПУ Линейная алгебра 1курс ИДЗ №3.doc
#
20.06.20141.09 Mб65ТПУ Линейная алгебра 1курс ИДЗ №4.doc