Добавил:
Vezen
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:Кузнецов_математика
.pdf
Соседние файлы в предмете Высшая математика




 xy, z = 0.
xy, z = 0.
 xy, z = 0.
xy, z = 0.
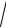 xy, z = 0.
xy, z = 0.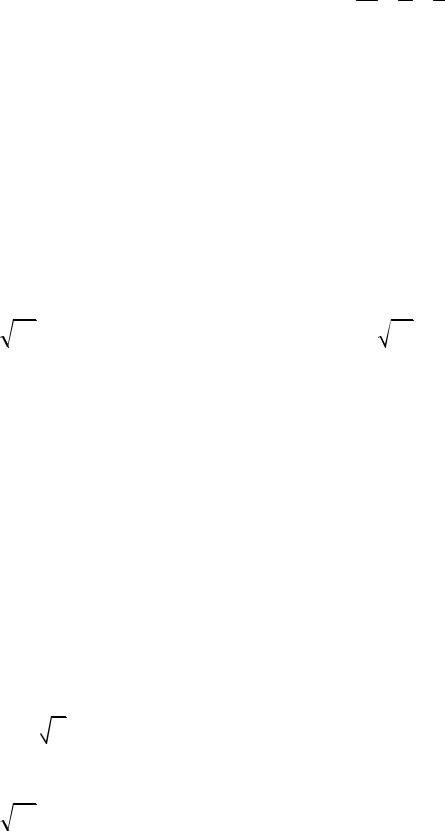

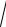 xy, z = 0.
xy, z = 0.
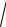 y
y 
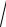 xy, z = 0.
xy, z = 0.
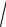 xy, z = 0.
xy, z = 0.
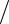 x, y
x, y 
 36
36 
 36
36 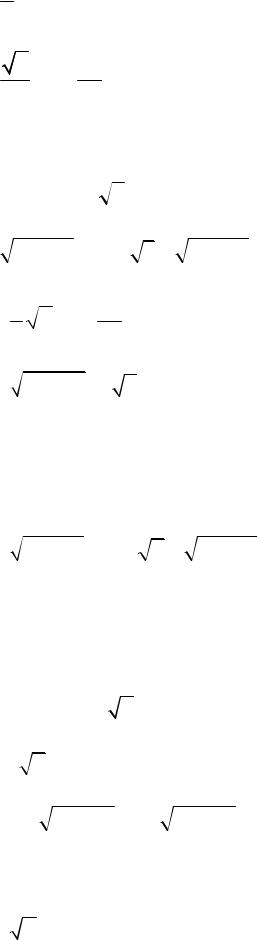

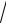 6y
6y 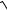
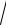 12
12 
 3
3 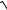
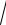 12
12 
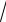 x, y
x, y 
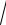 24
24 
 3y
3y 
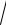 18
18
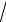 2
2 
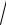 18
18 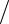 x, y
x, y 
 2y
2y 
 x, y
x, y  x, x
x, x 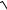
 36
36 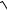
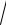 36
36 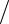 4
4 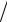 2.
2.
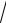 x, y
x, y 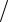 x, x
x, x 
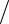 x, y = 7e
x, y = 7e
 72
72 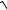
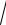 6
6 
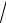 6
6 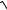
 6
6 
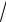 x, y
x, y 
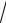 x, y
x, y  x, x
x, x 
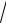 6
6 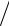

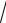 3, y
3, y 
 3x.
3x.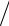

 3, y
3, y 
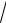 3x.
3x.

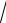 3.
3.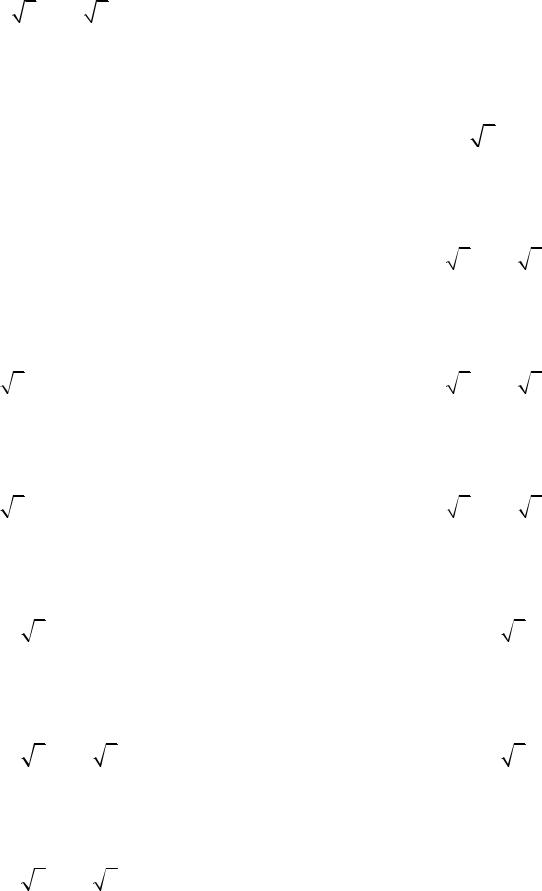
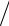

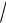 3, y
3, y 
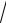 3x.
3x.
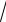 3x, x
3x, x 
 3x, x
3x, x 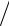

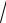 3, y
3, y 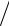

 3, y
3, y 
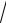 3x.
3x.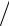

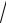 3, y
3, y 
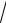 3x.
3x.
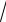 3x.
3x.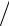

 3, y
3, y 
 3x.
3x.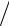

 3, y
3, y 
 3x.
3x.

 3, y
3, y 
 3x.
3x.

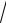 3.
3.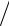

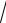 3.
3.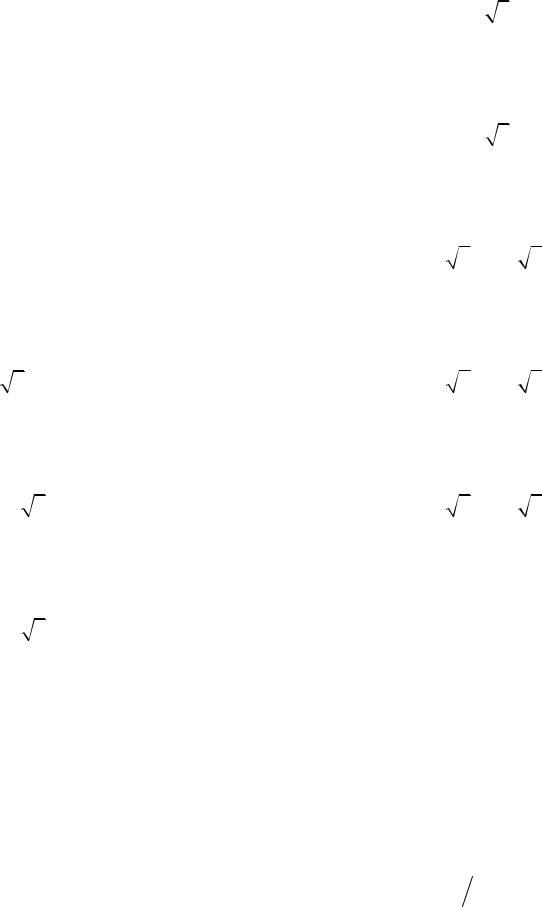

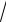 3x, x
3x, x 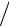

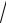 3, x
3, x 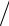

 3, x
3, x 
 3x.
3x.
 3x.
3x.

 3, y
3, y 
 3x.
3x.

 3, y
3, y 
 3x.
3x.

 3, y
3, y 
 3x.
3x.

 4
4  2.
2. 4
4 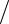 2
2 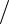 2.
2.