Добавил:

Vezen Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Коломенский институт филиал МГМУ

Предмет:

Высшая математика

Файл:

Кузнецов_математика

.pdf

Скачиваний:

414

Добавлен:

20.06.2014

Размер:

2.87 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 2710 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Задача 15. Вычислить площади фигур, ограниченных линиями, заданными уравнениями.

				3
	x = 4		2 cos	3	t,
	x = 4		2 cos		t,
	y = 2
15.1.	y = 2		2sin3 t,


	x = 2	(x ≥ 2).
	x = 4	(t − sint),

		(1− cost),
15.3.	y = 4	(1− cost),

	y = 4	(0 < x < 8π , y ≥ 4).
	x = 2cost,

15.5. y = 6sint,
	y = 3	(y ≥ 3).
		3

x =16cos t,

15.7. y = sin3 t,

x = 63 (x ≥ 63).

x = 3(t − sint),


15.9. y = 3(1− cost),

	y = 3	(0 < x < 6π , y ≥ 3).

			2cost,
	x = 2		2cost,


15.11.	y = 3		2sint,

	y = 3	(y ≥ 3).
				3
	x = 32cos			3	t,
	x = 32cos				t,

15.13.	y = sin3 t,

	x = 4	(x ≥ 4).
	x = 6	(t − sint),

		(1− cost),
15.15.	y = 6	(1− cost),

	y = 6	(0 < x <12π , y ≥ 6).


		2cost,
	x =	2cost,


15.2.	y = 2		2sint,

	y = 2	(y ≥ 2).

x =16cos3 t,

15.4. y = 2sin3 t,

x = 2 (x ≥ 2).

x = 2

(t − sint),

(1− cost),

15.6. y = 2

y = 3

(0 < x < 4π , y ≥ 3).

x = 6cost,

15.8. y = 2sint,

y =

(y ≥

x = 8

2cos

2sin3 t,

15.10.

y =

x = 4

(x ≥ 4).

x = 6

(t − sint),

(1− cost),

15.12.

y = 6

y = 9

(0 < x <12π , y ≥ 9).

x = 3cost,

15.14. y = 8sint,

y = 4

(y ≥ 4).

x = 8cos

15.16. y = 4sin3 t,

x = 33 (x ≥ 33).

15.17. y x

15.19. y x

15.21. y y

15.23. y y

15.25. y x

15.27. y y

15.29. y y

15.31. y x

=6cos3 t,

=4sin3 t,

=23 (x ≥ 23).

=22cos3 t,

=2sin3 t,

=1 (x ≥1).

=t − sint,

=1− cost,

=1 (0 < x < 2π , y ≥1).

=9cost,

=4sint,

=2 (y ≥ 2).

=24cos3 t,

=2sin3 t,

=93 (x ≥ 93).

=2(t − sint),

=2(1− cost),

= 2 (0 < x < 4π , y ≥ 2).

=22cost,

=52sint,

=5 (y ≥ 5).

=32cos3 t,

=3sin3 t,

=123 (x ≥123).

15.18. y y

15.20. y y

15.22. y x

15.24. y y

15.26. y y

15.28. y x

15.30. y y

=10(t − sint),

=10(1− cost),

=15 (0 < x < 20π , y ≥15).

=2cost,

=42sint,

=4 (y ≥ 4).

=8cos3 t,

=8sin3 t,

=1 (x ≥1).

=8(t − sint),

=8(1− cost),

=12 (0 < x <16π , y ≥12).

=3cost,

=8sint,

=43 (y ≥ 43).

=42cos3 t,

=2sin3 t,

=2 (x ≥ 2).

=4(t − sint),

=4(1− cost),

=6 (0 < x < 8π , y ≥ 6).

Задача 16. Вычислить площади фигур, ограниченных линиями, заданными в полярных координатах.


16.1. r = 4cos3ϕ,			r = 2 (r ≥ 2).

16.3.	r = 3cosϕ,		r = sinϕ,
	(0	≤ ϕ ≤ π 2).


16.5.	r = 2cosϕ,		r = 2 3sinϕ,
	(0	≤ ϕ ≤ π 2).

16.7. r = 6sin3ϕ,			r = 3 (r ≥ 3).

r= cosϕ,

16.9.r = 2sin(ϕ −π4),

(−π4 ≤ ϕ ≤ π2).

16.11. r = 6cos3ϕ, r = 3 (r ≥ 3).

r = cosϕ, r = sinϕ,

16.13. (0 ≤ ϕ ≤ π2).

16.15. r = cosϕ, r = 2cosϕ.

16.17. r =1+ 2cosϕ.

16.19. r =1+ 2sinϕ.

16.21. r = (32)cosϕ, r = (52)cosϕ.

16.23. r = sin6ϕ.

16.25. r = cosϕ + sinϕ.

16.27. r = 2cos6ϕ.

16.2. r = cos2ϕ.

16.4. r = 4sin3ϕ, r = 2 (r ≥ 2).

16.6. r = sin3ϕ.

16.8. r = cos3ϕ.

r= sinϕ,

16.10.r = 2 cos(ϕ −π4), (0 ≤ ϕ ≤ 3π4).

16.12. r =12 + sinϕ.

r= 2cos(ϕ −π4),

16.14.r = 2sin(ϕ −π4), (π4 ≤ ϕ ≤ 3π4).

16.16. r = sinϕ, r = 2sinϕ.

16.18. r =12 + cosϕ.

16.20. r = (52)sinϕ, r = (32)sinϕ.

16.22. r = 4cos4ϕ.

16.24. r = 2cosϕ, r = 3cosϕ.

16.26. r = 2sin4ϕ.

16.28. r = cosϕ − sinϕ.

16.29.	r = 3sinϕ,	r = 5sinϕ.	16.30. r = 2sinϕ, r = 4sinϕ.
16.31.	r = 6sinϕ,	r = 4sinϕ.

Задача 17. Вычислить длины дуг кривых, заданных уравнениями в прямоугольной системе координат.

17.2. y =

−

ln x

17.1. y = ln x,

3 ≤ x ≤

15.

1≤ x ≤ 2.

17.3. y =

1− x2

+ arcsin x,

0 ≤ x ≤ 7 9.

17.3. y = ln

3 ≤ x ≤

17.5. y = −lncos x,

0 ≤ x ≤ π 6.

17.6. y = ex + 6,

8 ≤ x ≤ ln

15.

17.7. y = 2 + arcsin

x +

x − x2 ,

1 4 ≤ x ≤1.

(

)

17.8. y = ln

2 ≤ x ≤ 3.

−1 ,

(

)

17.9. y =

1− x2

+ arccos x,

0 ≤ x ≤ 8 9.

− x2

0 ≤ x ≤1 4.

17.10. y = ln 1

17.11. y = 2 + ch x,

0 ≤ x ≤1.

17.12. y =1− lncos x, 0 ≤ x ≤ π 6.

17.13. y = ex +13,

15 ≤ x ≤ ln

24.

17.14. y = −arccos

x +

x − x2 ,

0 ≤ x ≤1 4.

17.15. y = 2 − ex ,

3 ≤ x ≤ ln

17.16. y = arcsin x −

1− x2 ,

0 ≤ x ≤15 16.

(

)

17.17. y =1− lnsin x,

π 3 ≤ x ≤ π

17.18. y =1− ln

≤ x

≤ 4.

−1 , 3

17.19. y =

x − x2 − arccos

x + 5,

1 9 ≤ x ≤1.

17.20. y = −arccos x +

1− x2 +1,

0 ≤ x ≤ 9 16.

17.21. y = lnsin x,

π 3 ≤ x ≤ π 2.

17.22. y = ln7 − ln x,

3 ≤ x ≤

17.23. y = ch x + 3,

0 ≤ x ≤1.

17.24. y =1+ arcsin x −

1− x2 ,

0 ≤ x ≤ 3 4.

17.25. y = lncos x + 2,

0 ≤ x ≤ π 6.

ex + e−x

17.26. y = ex + 26,

8 ≤ x ≤ ln

24.

17.27. y =

+ 3,

0 ≤ x ≤ 2.

17.28. y = arccos

x −

x − x2 + 4,

0 ≤ x ≤1 2.

ex + e−x

+ 3

17.29. y =

0 ≤ x ≤ 2.

17.30. y = ex + e,

3 ≤ x ≤ ln 15.

17.31. y =

1− ex − e− x

0 ≤ x ≤ 3.

Задача 18. Вычислить длины дуг кривых, заданных параметрическими

уравнениями.

	x = 5(t − sint),

18.1.	y	= 5	(1− cost),


			0 ≤ t ≤ π.
	x = 4		(cost + tsint),

18.3.	y	= 4	(sint − tcost),


			0 ≤ t ≤ 2π.
				3
	x =10cos				t,
		=10sin3 t,
18.5. y		=10sin3 t,

	0 ≤ t ≤ π 2.
	x = 3(t − sint),

18.7.	y	= 3(1− cost),


		π ≤ t ≤ 2π.
	x = 3(cost + tsint),

		= 3(sint − tcost),
18.9.	y	= 3(sint − tcost),

0 ≤ t ≤ π3.

	x = 3(2cost − cos2t),

18.2.	y = 3(2sint − sin2t),


					0 ≤ t ≤ 2π.
	x = (t2 − 2)sint + 2tcost,
18.4.		(2 − t2 )cost + 2tsint,
18.4.	y =	(2 − t2 )cost + 2tsint,

								0 ≤ t ≤ π.
		t		(cost + sint),
	x = e			(cost + sint),
18.6.	y = et				(cost − sint),


					0 ≤ t ≤ π.
		1				1
	x =		cost −					cos2t,
	x =	2	cost −				4	cos2t,
18.8.		1				1
18.8.		1				1
	y =			sint −				sin2t,
	y =			sint −				sin2t,
		2				4
		π 2 ≤ t ≤ 2π 3.
	x = (t2 − 2)sint + 2tcost,
					2 − t2 )cost + 2tsint,
18.10. y = (					2 − t2 )cost + 2tsint,

0 ≤ t ≤ π3.

				3
	x = 6cos			3	t,
	x = 6cos				t,
		= 6sin3 t,
18.11. y		= 6sin3 t,

	0 ≤ t ≤ π 3.
	x = 2,5(t − sint),

		= 2,5(1− cost),
18.13.	y	= 2,5(1− cost),

		π 2 ≤ t ≤ π.
	x = 6(cost + tsint),

18.15.	y = 6		(sint − tcost),


					0 ≤ t ≤ π.
				3
	x = 8cos				t,
		= 8sin3 t,
18.17. y		= 8sin3 t,

	0 ≤ t ≤ π 6.
	x = 4		(t − sint),

		= 4	(1− cost),
18.19.	y	= 4	(1− cost),

	π 2 ≤ t ≤ 2π 3.
	x = 8(cost + tsint),

		= 8	(sint − tcost),
18.21.	y	= 8	(sint − tcost),

			0 ≤ t ≤ π 4.
				3
	x = 4cos				t,
		= 4sin3 t,
18.23. y		= 4sin3 t,

	π 6 ≤ t ≤ π 4.
	x = 2		(t − sint),

		= 2	(1− cost),
18.25.	y	= 2	(1− cost),

		0 ≤ t ≤ π 2.
	x = 2		(cost + tsint),

		= 2	(sint − tcost),
18.27.	y	= 2	(sint − tcost),

0 ≤ t ≤ π2.

		t		(cost + sint),
	x = e			(cost + sint),
18.12.	y = et (cost − sint),


					π 2 ≤ t ≤ π.
	x = 3,5				(2cost − cos2t),

					(2sint − sin2t),
18.14.	y = 3,5				(2sint − sin2t),

					0 ≤ t ≤ π 2.
	x = (t2 − 2)sint + 2tcost,

18.16.	y = (2 − t2 )cost + 2tsint,

					0 ≤ t ≤ π 2.
		t		(cost + sint),
	x = e			(cost + sint),
18.18.	y = et (cost − sint),


					0 ≤ t ≤ 2π.
	x = 2		(2cost − cos2t),

				(2sint − sin2t),
18.20.	y = 2			(2sint − sin2t),

					0 ≤ t ≤ π 3.
	x = (t2 − 2)sint + 2tcost,

18.22.	y = (2 − t2 )cost + 2tsint,

					0 ≤ t ≤ 2π.
		t		(cost + sint),
	x = e			(cost + sint),
18.24.	y = et (cost − sint),


				0 ≤ t ≤ 3π 2.
	x = 4		(2cost − cos2t),

18.26.	y = 4			(2sint − sin2t),


					0 ≤ t ≤ π.
	x = (t2 − 2)sint + 2tcost,

18.28.	y = (2 − t2 )cost + 2tsint,

0 ≤ t ≤ 3π.

	x = 2cos3 t,		x = et (cost + sint),

				y = et (cost − sint),
18.29. y = 2sin3 t,		18.30.		y = et (cost − sint),


	0 ≤ t ≤ π 4.			π 6 ≤ t ≤ π 4.
	x = (t2 − 2)sint + 2tcost,

18.31.	y = (2 − t2 )cost + 2tsint,

0 ≤ t ≤ π.

Задача 19. Вычислить длины дуг кривых, заданных уравнениями в полярных координатах.

19.1. ρ = 3e3ϕ 4 ,

−π 2 ≤ ϕ ≤ π 2.

19.2. ρ = 2e4ϕ 3,

−π 2 ≤ ϕ ≤ π 2.

19.3. ρ =

19.4. ρ = 5e5ϕ 12 ,

2eϕ ,

−π 2 ≤ ϕ ≤ π 2.

19.5. ρ = 6e12ϕ 5,

−π 2 ≤ ϕ ≤ π 2.

19.6. ρ = 3e3ϕ 4 ,

0 ≤ ϕ ≤ π 3.

19.7. ρ = 4e4ϕ 3,

19.8. ρ =

0 ≤ ϕ ≤ π 3.

2eϕ ,

0 ≤ ϕ ≤ π 3.

19.9. ρ = 5e5ϕ 12 ,

0 ≤ ϕ ≤ π 3.

19.10. ρ =12e12ϕ 5, 0 ≤ ϕ ≤ π 3.

19.11. ρ =1− sinϕ, −π 2 ≤ ϕ ≤ −π 6.

19.12.

ρ = 2(1− cosϕ ),

−π ≤ ϕ ≤ −π 2.

19.13. ρ = 3(1

+ sinϕ ),

−π 6 ≤ ϕ ≤ 0.

19.14. ρ = 4

(1− sinϕ ),

0 ≤ ϕ ≤ π 6.

19.15. ρ = 5

− cosϕ ),

−π 3 ≤ ϕ ≤ 0.

19.16. ρ = 6

(1+ sinϕ ),

−π 2 ≤ ϕ ≤ 0.

19.17. ρ = 7

(1− sinϕ ),

−π 6 ≤ ϕ ≤ π 6.

19.18. ρ = 8

− cosϕ ),

− 2π 3 ≤ ϕ ≤ 0.

19.19. ρ = 2ϕ,	0	≤ ϕ ≤ 3 4.	19.20. ρ = 2ϕ,	0	≤ ϕ ≤ 4 3.
19.21. ρ = 2ϕ,	0	≤ ϕ ≤ 5 12.	19.22. ρ = 2ϕ,	0	≤ ϕ ≤12 5.
19.23. ρ = 4ϕ,	0	≤ ϕ ≤ 3 4.	19.24. ρ = 3ϕ,	0	≤ ϕ ≤ 4 3.
19.25. ρ = 5ϕ,	0 ≤ ϕ ≤12 5.		19.26. ρ = 2cosϕ,		0 ≤ ϕ ≤ π 6.
19.27. ρ = 8cosϕ,		0 ≤ ϕ ≤ π 4.	19.28. ρ = 6cosϕ,		0 ≤ ϕ ≤ π 3.
19.29. ρ = 2sinϕ,		0 ≤ ϕ ≤ π 6.	19.30. ρ = 8sinϕ,		0 ≤ ϕ ≤ π 4.

19.31. ρ = 6sinϕ, 0 ≤ ϕ ≤ π3.

Задача 20. Вычислить объемы тел, ограниченных поверхностями.

20.1.

+ y2

=1,

z = y,

z = 0 (y ≥ 0).

20.2. z = x2 + 4y2 ,

z = 2.

20.3.

− z2

=1,

z = 0,

z = 3.

20.4.

−

= −1,

z =12.

20.5.

=1,

z =1,

z = 0.

20.6. x2 + y2 = 9,

z = y,

z = 0

(y ≥ 0).

20.7. z = x2 + 9y2 , z = 3.

20.8.

+ y2 − z2 =1, z = 0, z = 3.

20.9.

−

= −1,

z =16.

20.10.

=1, z = 2, z = 0.

=1,

z = y

z = 0 (y ≥ 0).

20.12. z = 2x2 + 8y2 , z = 4.

20.11.

20.13.

− z2

=1,

z = 0,

z = 2.

20.14.

−

= −1,

z =12.

20.15.

=1,

z = 3,

z = 0.

=1,

z = y

z = 0

(y ≥ 0).

20.16.

20.17. z = x2 + 5y2 ,

z = 5.

20.18.

− z2 =1,

z = 0,

z = 4.

20.19.

−

= −1,

z = 20.

20.20.

=1,

z = 4,

z = 0.

100

20.21.

=1,

z =

, z = 0 (y ≥ 0).

20.22. z = 4x2 + 9y2 ,

z = 6.

20.23. x2 +

− z2 =1,

z = 0,

z = 3.

20.24.

−

= −1,

z = 20.

100

20.25.

=1,

z = 5,

z = 0.

100

20.26.

+ y2

=1,

z =

z = 0 (y ≥ 0).

20.27. z = 2x2 +18y2 , z = 6.

20.28.

− z2

=1,

z = 0,

z = 2.

20.29.

−

= −1,

z =16.

20.30.

=1, z = 6,

z = 0.

144

20.31.

=1,

z = 7,

z = 0.

196

Задача 21. Вычислить объемы тел, образованных вращением фигур, ограниченных графиками функций. В вариантах 1–16 ось вращения Ox, в вариантах 17–31 ось

вращения Oy.

21.1. y = −x2 + 5x − 6,

y = 0.

21.2. 2x − x2 − y = 0,

2x2 − 4x + y = 0.

21.3. y = 3sin x,

y = sin x, 0 ≤ x ≤ π.

21.4. y = 5cos x,

y = cos x,

x = 0, x ≥ 0.

21.5. y = sin2 x,

x = π 2,

y = 0.

21.6. x = 3 y − 2,

x =1,

y =1.

21.7. y = xex ,

y = 0,

x =1.

21.8. y = 2x − x2 ,

y = −x + 2,

x = 0.

21.9. y = 2x − x2 ,

y = −x + 2.

21.10. y = e1−x ,

y = 0,

x = 0,

x =1.

21.11. y = x2 ,

y2 − x = 0.

21.12. x2 + ( y − 2)2

=1.

21.14. y = x2 ,

y =1,

x = 2.

21.13. y =1− x2 ,

x = 0,

x = y − 2,

x =1.

21.15. y = x3,

y =

21.16. y = sin(π x 2),

y = x2.

21.17. y = arccos(x 3),

y = arccos x,

y = 0.

21.18.

y = arcsin(x 5),

y = arcsin x,

y = π 2.

21.19. y = x2 ,

x = 2,

y = 0.

21.20. y = x2 +1,

y = x,

x = 0,

y = 0.

21.21. y = x −1,

y = 0,

y =1, x = 0,5. 21.22. y = ln x,

x = 2,

y = 0.


21.23. y = (x −1)2 ,		y =1.		21.24.
y2 = x − 2, y = 0, y = x3, y =1.
21.25. y = x3,	y = x2.		21.26. y = arccos(x 5), y = arccos(x 3),		y = 0.
21.27. y = arcsin x,		y = arccos x,		y = 0. 21.28. y = x2 − 2x +1, x = 2,	y = 0.
21.29. y = x3,	y = x.			21.30.
y = arccos x,	y = arcsin x,		x = 0.
21.31. y = (x −1)2 ,		x = 0,	x = 2,	y = 0.

		Задача 22
		Варианты 1–10
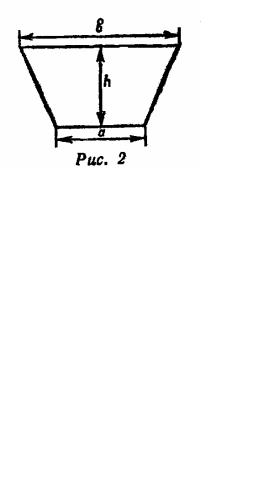
Вычислить силу, с которой вода давит на плотину,
Вычислить силу, с которой вода давит на плотину,
сечение которой имеет форму равнобочной трапеции (рис. 2).
Плотность воды	ρ =1000	кг/м3, ускорение свободного
падения g положить равным 10 м/с2.
У к а з а н и е. Давление на глубине x равно ρgx.

22.1. a = 4,5 м,	b = 6,6 м,	h = 3,0 м.	22.2. a = 4,8 м,		b = 7,2 м,		h = 3,0 м.
22.3. a = 5,1 м,	b = 7,8 м,	h = 3,0 м.	22.4. a = 5,4 м,		b = 8,4 м,		h = 3,0 м.
22.5. a = 5,7 м,	b = 9,0 м,	h = 4,0 м.	22.6. a = 6,0 м,		b = 9,6 м,		h = 4,0 м.
22.7. a = 6,3 м,	b =10,2 м,	h = 4,0 м.
		22.8. a = 6,6 м,		b =10,8 м,		h = 4,0 м.
22.9. a = 6,9 м,	b =11,4 м,	h = 5,0 м.
		22.10. a = 7,2 м,		b =12,0 м,		h = 5,0 м.

Варианты 11–20

Определить работу (в джоулях), совершаемую при подъеме спутника с поверхности Земли на высоту H км. Масса спутника равна m т, радиус Земли

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 2710 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете Высшая математика

#
20.06.2014380.9 Кб76Доказательства по линейной алгебре.docx
#
20.06.20142.87 Mб414Кузнецов_математика.pdf
#
20.06.2014951.81 Кб530Ответы на вопросы к экзамену по математике (шпаргалки).doc
#
20.06.20142.31 Mб180ТПУ Линейная алгебра 1курс ИДЗ №1.doc
#
20.06.2014380.42 Кб65ТПУ Линейная алгебра 1курс ИДЗ №2.doc
#
20.06.2014539.14 Кб58ТПУ Линейная алгебра 1курс ИДЗ №3.doc
#
20.06.20141.09 Mб66ТПУ Линейная алгебра 1курс ИДЗ №4.doc