2.6 Метод квадратного корня решения симметричных слау

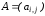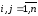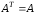СЛАУ (2.4) называется симметричной, если матрица ее коэффициентов ,, симметричная, т.е. если. Симметричная СЛАУ вполне может быть решена методом Гаусса. Однако если для решения симметричной СЛАУ воспользоваться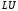-разложением (схемой Холецкого), то объем вычислений можно сократить почти вдвое. Ввиду симметричности матрицы схема Холецкого упрощается по сравнению со случаем матрицы общего вида.

Будем строить представление симметричной матрицы в виде . Запишем это разложение в развернутом виде:

.

Умножая матрицы в левой части и приравнивая соответствующие элементы обеих частей, получим систему 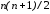уравнений относительно такого же количества неизвестных (элементов матрицы):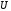

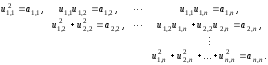
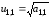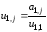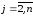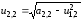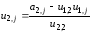Из первой строки уравнений находим сначала , затемпри. Из второй –, затемпри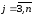, и т.д. Завершается процесс вычислением

.

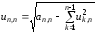Таким образом, матрица 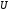может быть определена совокупностью формул

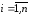,, (2.21)

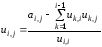,,, (2.22)

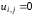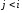,. (2.23)

Известно, что для важного в приложениях класса симметричных положительно определенных матриц разложение по формулам (2.21) – (2.23) выполнимо.

При наличии разложения 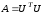мы можем вместо уравнения (2.4) записать эквивалентное уравнение

.

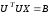Введя вектор вспомогательных переменных 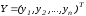, перепишем его в виде системы

,

.

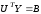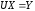Первое уравнение этой системы имеет вид

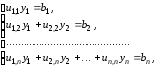
откуда получаем

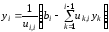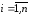,. (2.24)

Из второго уравнения

находим искомые значения :

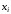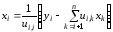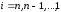,. (2.25)

Решение симметричных СЛАУ по формулам (2.21) – (2.25) называют методом квадратного корня.

2.7 Метод Гаусса–Зейделя

Метод Гаусса-Зейделя – это итерационный метод решения задачи, или метод последовательных приближений.

2.7.1 Расчетные формулы метода Гаусса–Зейделя

Получим расчетные формулы метода Гаусса–Зейделя. Пусть решается система уравнений (2.1). Выразим из 1-го уравн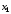ения , из 2-го уравнения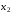и т.д. В результате получим

,

,

…………………………………………….

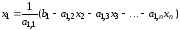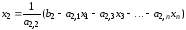или вообще для любого

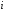
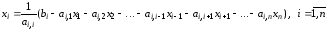. (2.26)

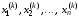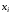Предположим, что на некоторой -й итерации мы получили решение. Используем известные к моменту расчетазначения этих переменных в правой части уравнения (2.26) для расчета значения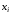в левой части. В результате мы получим следующую рекуррентную формулу, которая и составляет метод Гаусса–Зейделя:

.

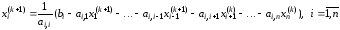Расчеты по последней формуле продолжаются при 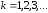до тех пор, пока не будет выполняться условие

,

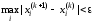или условие

,

где 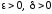, причем– допустимая абсолютная погрешность нахождения

решения СЛАУ, а 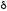– допустимая относительная погрешность.

2.7.2 Сходимость метода Гаусса–Зейделя

Итерационные методы могут сходиться к решению или не сходиться. То же самое относится и к методу Гаусса–Зейделя. Исследуем сходимость метода на примере системы из двух уравнений

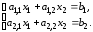
Запишем данную систему в виде

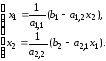(2.27)

Итерации метода Гаусса–Зейделя здесь осуществляются по формулам

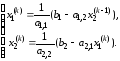(2.28)

Обозначим

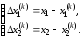
Вычитая из выражений (2.27) выражения (2.28), получим

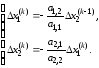
Подставляя первое из этих выражений во второе, получим

.

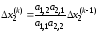Аналогично можно найти

,

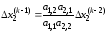так что

.

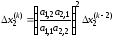Продолжая этот процесс дальше, будем иметь

.

Точно так же можно получить

.

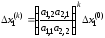Поэтому если

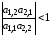, (2.29)

то ,,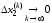 и метод Гаусса-Зейделя сходится к решению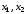. Соотношение (2.29) – это достаточное условие сходимости метода Гаусса–Зейделя для системы из двух уравнений.

Содержательный смысл приведенного условия сходимости можно выяснить, проанализировав его. Неравенство (2.29) выполняется, если

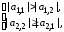
или если

Последние два условия можно назвать условиями преобладания диагональных

элементов системы уравнений: для сходимости метода Гаусса–Зейделя диагональные элементы системы уравнений по абсолютной величине должны превышать недиагональные.

Полученные достаточные условия сходимости для системы двух уравнений можно распространить на систему уравнений. Без доказательства скажем, что метод Гаусса–Зейделя сходится для системыуравнений, если выполняются условия

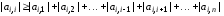
для всех 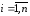кроме одного, для которого выполняется более жесткое условие

.

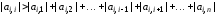Сформулированные условия также являются достаточными, но не необходимыми. Возможны случаи невыполнения данных условий при сходимости метода. Эти условия также можно назвать условиями преобладания диагональных элементов. В связи с этим часто для обеспечения сходимости метода Гаусса–Зейделя бывает достаточно поменять местами уравнения системы с тем, чтобы на главную диагональ матрицы системы попали наибольшие по абсолютному значению коэффициенты.