1.4 Погрешности арифметических операций

Погрешность, возникшая в определенном месте вычислений, распространяется дальше в процессе вычислений. При этом может произойти накопление погрешности до больших значений, что может поставить под сомнение конечный результат. В связи с этим весьма важным является вопрос анализа погрешностей вычислений и их распространения в вычислениях, который рассматривается ниже.

Пусть 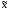– приближенное значение числа.Абсолютной погрешностью числа называется разность его точного и приближенного значений

.

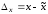Это значит, что точное значение числа равно сумме приближенного значения и абсолютной погрешности:

.

Относительная погрешность числа определяется как отношение абсолютной погрешности к приближенному значению:

.

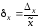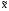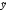Поскольку в численных методах используются арифметические операции, то определим абсолютные и относительные погрешности операций сложения, вычитания, умножения и деления. Пусть и– приближенные значения чиселисоответственно, а также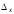и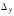– их абсолютные погрешности, так что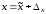,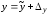. Найдем абсолютные погрешности арифметических операций.

Для сложения получим

.

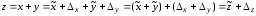Мы видим, что абсолютная погрешность суммы равна сумме абсолютных погрешностей слагаемых:

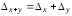. (1.1)

Аналогично для вычитания получаем

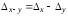. (1.2)

Для операции умножения будем иметь

.

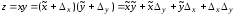В этом выражении произведением погрешностей 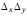по сравнению с другими слагаемыми можно пренебречь:

.

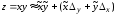Отсюда погрешность умножения

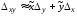. (1.3)

Абсолютную погрешность деления определим как линейную часть приращения функции двух переменных

.

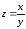Для этого представим функцию линейной частью ряда Тейлора в окрестности приближенных значений 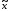,. Получим

.

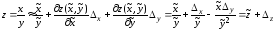Следовательно, абсолютная погрешность деления

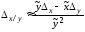. (1.4)

Получим также выражения для относительных погрешностей арифметических операций.

Для сложения имеем

,

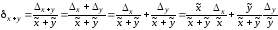следовательно,

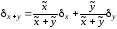. (1.5)

Аналогично получаем для операции вычитания:

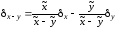. (1.6)

Для операции умножения имеем

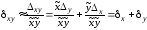, (1.7)

и для операции деления

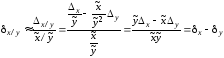. (1.8)

Таким образом, мы получили формулы (1.1) – (1.4) для абсолютных погрешностей и формулы (1.5) – (1.8) для относительных погрешностей арифметических операций. Знак минус в этих формулах не означает уменьшения погрешности, поскольку знак абсолютной или относительной погрешности может быть любым.

Часто нас интересует абсолютное значение погрешности. Для оценки абсолютных значений погрешности обычно используются неравенства. Приведем некоторые неравенства и равенства относительно абсолютных значений, известные из курса школьной математики:

,

,

,

.

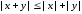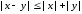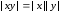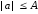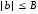Если и, то,.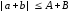

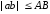С учетом этих выражений, в частности, получаем, что

,

.

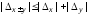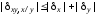Отметим, что мы нашли погрешности арифметических операций, считая, что эти операции выполняются абсолютно точно. Так как в каждой из них существует относительная погрешность округления , то ее нужно добавить отдельно к полученным относительным погрешностям арифметических операций.