
- •Теоретический раздел Предисловие
- •Предисловие ко второму изданию
- •1 Математические модели. Численные методы. Погрешности вычислений
- •1.1 Математические модели и моделирование
- •1.2 Этапы численного решения задач на эвм
- •1.3 Виды погрешностей решения задач
- •1.4 Погрешности арифметических операций
- •1.5 Графы арифметических операций
- •1.6 Распространение погрешностей в вычислениях
- •2 Решение систем линейных алгебраических уравнений
- •2.1 Постановка задачи. Методы решения
- •2.2 Метод Гаусса
- •2.2.1 Описание метода Гаусса
- •2.2.2 Расчетные формулы метода Гаусса
- •2.2.3 Погрешность метода Гаусса. Метод Гаусса с выбором главного элемента
- •2.3 Вычислительная сложность метода Гаусса
- •2.4 Обращение матрицы
- •2.5 Метод lu-разложения
- •2.6 Метод квадратного корня решения симметричных слау
- •2.7 Метод Гаусса–Зейделя
- •2.7.1 Расчетные формулы метода Гаусса–Зейделя
- •2.7.2 Сходимость метода Гаусса–Зейделя
- •2.7.3 Графическая иллюстрация метода Гаусса–Зейделя
- •3 Аппроксимация функций
- •3.1 Понятие аппроксимации функций
- •3.2 Постановка задачи интерполирования функций
- •3.3 Интерполяционный полином Лагранжа
- •3.4 Вычисление значений полиномов
- •3.5 Вычислительная сложность задачи интерполирования
- •3.6 Конечные и разделенные разности функции
- •3.7 Интерполяционный полином Ньютона
- •3.8 Погрешность интерполирования
- •3.9 Полиномы Чебышева 1-го рода
- •3.10 Наилучший выбор узлов интерполирования
- •4 Численное интегрирование
- •4.1 Постановка задачи численного интегрирования
- •4.2 Метод прямоугольников
- •4.3 Погрешность метода прямоугольников
- •4.4 Метод трапеций
- •4.5 Погрешность метода трапеций
- •4.6 Метод Симпсона
- •4.7 Погрешность метода Симпсона
- •4.8 Интерполяционные квадратурные формулы
- •4.9 Интерполяционные квадратурные формулы наивысшей алгебраической степени точности (квадратурные формулы Гаусса)
- •4.9.1 Квадратурная формула Гаусса–Лежандра
- •4.9.2 Квадратурная формула Гаусса–Лагерра
- •4.9.3 Квадратурная формула Гаусса–Эрмита
- •5 Решение нелинейных уравнений
- •5.1 Постановка задачи численного решения нелинейных уравнений
- •5.2 Метод деления отрезка пополам
- •5.3 Метод хорд
- •5.4 Метод простой итерации
- •5.5 Метод Ньютона
- •5.6 Метод секущих
- •6 Решение обыкновенных дифференциальных уравнений
- •6.1 Постановка задачи
- •6.2 Метод рядов Тейлора
- •6.3 Метод Эйлера
- •6.4 Метод Рунге–Кутта 2-го порядка
- •6.5 Метод Рунге–Кутта 4-го порядка
- •7 Решение систем обыкновенных дифференциальных уравнений
- •7.1 Постановка задачи
- •7.2 Приведение дифференциального уравнения -го порядка к системе дифференциальных уравнений 1-го порядка
- •7.3 Метод Эйлера
- •8.2 Выполнение символьных операций в Matlab
- •8.3 Создание символьных переменных
- •8.4 Создание группы символьных переменных
- •8.5 Создание списка символьных переменных
- •8.6 Вывод символьного выражения
- •8.7 Упрощение выражений
- •8.8 Вычисление производных
- •8.9 Вычисление интегралов
- •8.10 Вычисление сумм рядов
- •8.11 Вычисление пределов
- •8.12 Разложение функции в ряд Тейлора
- •8.13 Вычисление определителя матрицы, обращение матрицы
- •9 Дополнение
- •9.1 Вычисление корней полиномов
- •9.2 Решение систем нелинейных уравнений. Метод Ньютона
- •9.3 Решение систем линейных алгебраических уравнений с трехдиагональной матрицей (метод прогонки)
- •9.4 Интерполирование функций сплайнами
- •Практический раздел Указания к выбору варианта
- •Лабораторная работа № 1. Работа в системе Matlab
- •1.1. Цель работы
- •1.2. Порядок выполнения работы
- •Лабораторная работа № 2. Решение систем линейных алгебраических уравнений
- •2.1. Цель работы
- •2.2. Теоретические положения
- •2.3. Порядок выполнения работы
- •Лабораторная работа № 3. Аппроксимация функций
- •3.1. Цель работы
- •3.2. Теоретические положения
- •3.3. Порядок выполнения работы
- •Лабораторная работа № 4. Численное интегрирование
- •4.1. Цель работы
- •4.2. Теоретические положения
- •4.3. Порядок выполнения работы
- •Лабораторная работа № 5. Решение нелинейных уравнений
- •5.1. Цель работы
- •5.2. Теоретические положения
- •5.3. Порядок выполнения работы
- •Лабораторная работа № 6. Решение обыкновенных дифференциальных уравнений
- •6.1. Цель работы
- •6.2. Теоретические положения
- •6.3. Порядок выполнения работы
- •Лабораторная работа № 7. Решение систем обыкновенных дифференциальных уравнений
- •7.1. Цель работы
- •7.2. Теоретические положения
- •7.3. Порядок выполнения работы
- •Лабораторная работа № 8. Выполнение символьных операций
- •8.1. Цель работы
- •8.2. Теоретические сведения
- •8.3. Порядок выполнения работы
- •Литература
- •Литература
6.2 Метод рядов Тейлора
Пусть
требуется решить дифференциальное
уравнение 1-го порядка (6.2). Запишем
разложение решения в ряд Тейлора в
окрестности некоторой точки
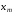 :
:
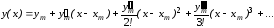 ,
(6.3)
,
(6.3)
где
 – значение функции
– значение функции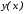 в точке
в точке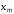 ;
; ,
, ,
,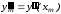 – значения производных функции
– значения производных функции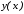 в точке
в точке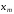 .
.
Предположим,
что мы нашли приближенное решение
уравнения (6.2) в точках
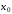 ,
,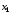 ,…,
,…,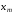 ,
расположенных на расстоянии
,
расположенных на расстоянии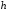 друг от друга, так что
друг от друга, так что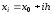 ,
,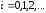 . Тогда мы можем найти приближенное
решение в точке
. Тогда мы можем найти приближенное
решение в точке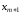 ,
подставив в выражение (6.3)
,
подставив в выражение (6.3) :
:
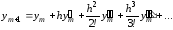 .
.
Чтобы воспользоваться этим выражением, нам необходимо ограничиться в нем конечным числом слагаемых и получить необходимые производные искомой функции, поскольку из постановки задачи они не известны. Ограничившись тремя слагаемыми, получим
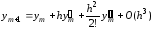 ,
(6.4)
,
(6.4)
где
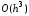 означает, что в отброшенные члены ряда
означает, что в отброшенные члены ряда входит в степени, не ниже третьей.
Покажем, как найти производные
входит в степени, не ниже третьей.
Покажем, как найти производные .
Непосредственно из дифференциального
уравнения (6.2) получаем, что
.
Непосредственно из дифференциального
уравнения (6.2) получаем, что
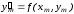 .
(6.5)
.
(6.5)
Дифференцируя
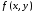 в правой части выражения (6.2) как сложную
функцию, явно зависящую от
в правой части выражения (6.2) как сложную
функцию, явно зависящую от ,
получим
,
получим
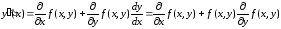 .
.
Обозначив
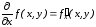 ,
,

и
предположив, что
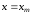 ,
,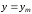 ,
получим
,
получим
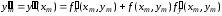 .
(6.6)
.
(6.6)
Подставив производные (6.5), (6.6) в выражение (6.4), получим следующую формулу решения уравнения (6.2) с помощью метода рядов Тейлора:
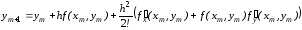 .
(6.7)
.
(6.7)
Формула
метода рядов Тейлора (6.7) характеризуется
следующим. Она является одношаговой,
так как для вычисления нового значения
функции
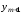 нам необходимо знать лишь предыдущее
значение функции
нам необходимо знать лишь предыдущее
значение функции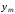 .
Абсолютная погрешность формулы имеет
порядок
.
Абсолютная погрешность формулы имеет
порядок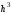 ,
поскольку при ее получении мы отбросили
в разложении Тейлора члены с
,
поскольку при ее получении мы отбросили
в разложении Тейлора члены с в кубе и выше. К ее недостаткам следует
отнести необходимость получения
производных
в кубе и выше. К ее недостаткам следует
отнести необходимость получения
производных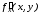 ,
,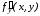 правой части решаемого уравнения (6.2) и
необходимость расчета значений трех
функций
правой части решаемого уравнения (6.2) и
необходимость расчета значений трех
функций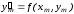 ,
, ,
, для получения нового значения функции
для получения нового значения функции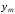 .
Ниже будут рассмотрены другие методы,
которые позволяют решить уравнение
(6.2) с той же точностью, что и формула
(6.7), но с меньшими вычислительными
затратами.
.
Ниже будут рассмотрены другие методы,
которые позволяют решить уравнение
(6.2) с той же точностью, что и формула
(6.7), но с меньшими вычислительными
затратами.
6.3 Метод Эйлера
Этот метод решения уравнения (6.2) состоит в последовательных расчетах по формуле
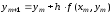 ,
(6.8)
,
(6.8)
начиная
с точки
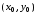 ,
заданной начальными условиями
,
заданной начальными условиями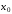 ,
,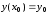 .
Здесь
.
Здесь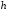 – шаг интегрирования по независимой
переменной
– шаг интегрирования по независимой
переменной .
Формула Эйлера (6.8) получается из формулы
(6.7) метода рядов Тейлора удержанием в
правой части лишь двух слагаемых.
.
Формула Эйлера (6.8) получается из формулы
(6.7) метода рядов Тейлора удержанием в
правой части лишь двух слагаемых.
Геометрический
смысл формулы Эйлера (6.3) иллюстрируется
на рисунке 6.1. В точке
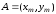 проводится касательная к интегральной
кривой
проводится касательная к интегральной
кривой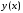 ,
новое значение функции
,
новое значение функции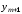 определяется как точка
определяется как точка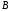 пересечения касательной с вертикальной
прямой
пересечения касательной с вертикальной
прямой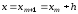 .
Следующая касательная проводится в
точке
.
Следующая касательная проводится в
точке .
Из рисунка видно, что при возрастании
переменной
.
Из рисунка видно, что при возрастании
переменной погрешность в определении функции может
накапливаться. Абсолютная погрешность
формулы Эйлера имеет порядок
погрешность в определении функции может
накапливаться. Абсолютная погрешность
формулы Эйлера имеет порядок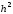 ,
что видно из формулы (6.7).
,
что видно из формулы (6.7).

Рисунок 6.1 – Иллюстрация метода Эйлера
6.4 Метод Рунге–Кутта 2-го порядка
Этот метод состоит в том, чтобы организовать последовательные расчеты по формулам
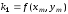 ,
,
 ,
(6.9)
,
(6.9)
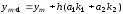 ,
,
начиная
с начальных условий
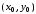 .
Здесь
.
Здесь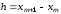 – шаг по переменной
– шаг по переменной ,
постоянный при всех
,
постоянный при всех ,
,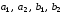 – некоторые коэффициенты, которые
надлежит выбрать. Обычно коэффициенты
– некоторые коэффициенты, которые
надлежит выбрать. Обычно коэффициенты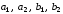 выбираются путем сравнения формул (6.9)
по точности с формулами метода рядов
Тейлора.
выбираются путем сравнения формул (6.9)
по точности с формулами метода рядов
Тейлора.
Получим формулы (6.9), имеющие ту же точность, что и формула рядов Тейлора (6.7). Для этого запишем формулы (6.9) в виде одной формулы:
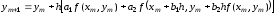 .
(6.10)
.
(6.10)
Далее
представим правую часть нашего уравнения
(6.2), т.е. функцию двух аргументов
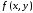 ,
линейной частью ряда Тейлора в окрестности
точки
,
линейной частью ряда Тейлора в окрестности
точки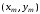 :
:
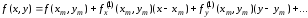
и положим здесь
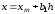 ,
,
 .
.
Получим
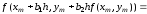
 .
(6.11)
.
(6.11)
Подставляя (6.11) в правую часть выражения (6.10), будем иметь
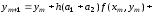
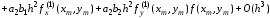 .
(6.12)
.
(6.12)
Приравняем
формулы (6.7) и (6.12). Для совпадения членов
с множителем
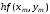 необходимо выполнить равенство
необходимо выполнить равенство
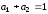 .
(6.13)
.
(6.13)
Для
совпадения членов с множителем
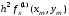 необходимо, чтобы
необходимо, чтобы
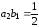 ,
(6.14)
,
(6.14)
а
для совпадения членов с множителем
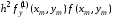 необходимо, чтобы
необходимо, чтобы
 .
(6.15)
.
(6.15)
Мы
получили 3 уравнения (6.13), (6.14), (6.15) с
четырьмя неизвестными
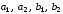 .
Следовательно, одно из этих неизвестных
можно выбрать произвольно. Выберем,
например,
.
Следовательно, одно из этих неизвестных
можно выбрать произвольно. Выберем,
например,
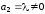 ,
,
 .
.
Тогда
 ,
,
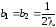 .
.
Соотношения (6.9) теперь примут вид
 ,
,
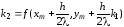 ,
(6.16)
,
(6.16)
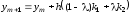 .
.
Формулы
(6.16) обеспечивают погрешность порядка
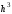 при любом
при любом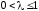 .
.
При
 получаем следующую наиболее употребительную
форму метода Рунге–Кутта 2-го порядка:
получаем следующую наиболее употребительную
форму метода Рунге–Кутта 2-го порядка:
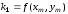 ,
,
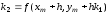 ,
(6.17)
,
(6.17)
 .
.
Графически
формулы (6.17) представлены на рисунке
6.2. В точке
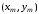 проводится касательная к интегральной
кривой
проводится касательная к интегральной
кривой (прямая
(прямая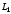 )
и определяется тангенс угла наклона
(угловой коэффициент) этой касательной
)
и определяется тангенс угла наклона
(угловой коэффициент) этой касательной .
Аналогично методу Эйлера определяется
новая точка
.
Аналогично методу Эйлера определяется
новая точка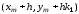 .
В этой точке проводится касательная с
угловым коэффициентом
.
В этой точке проводится касательная с
угловым коэффициентом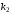 (прямая
(прямая ).
Новое значение функции
).
Новое значение функции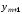 определяется как точка пересечения
касательной с усредненным угловым
коэффициентом
определяется как точка пересечения
касательной с усредненным угловым
коэффициентом
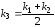
(прямая
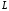 ,
параллельная прямой
,
параллельная прямой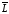 )
и вертикальной прямой
)
и вертикальной прямой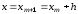 .
.
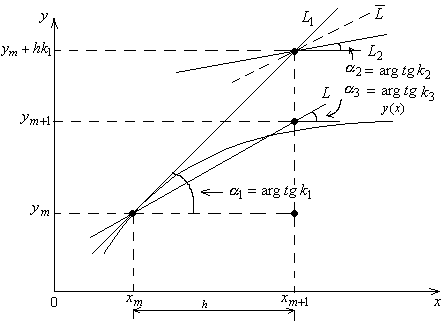
Рисунок 6.2 – Иллюстрация метода Рунге–Кутта 2-го порядка
При
 получаем следующую форму метода
Рунге–Кутта 2-го порядка:
получаем следующую форму метода
Рунге–Кутта 2-го порядка:
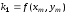 ,
,
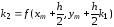 ,
,
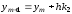 .
.
При
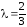 будем иметь формулы
будем иметь формулы
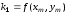 ,
,
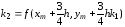 ,
,
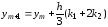 ,
,
которые обеспечивают наименьший верхний предел погрешности.
Отметим,
что метод Рунге–Кутта 2-го порядка хотя
и имеет ту же погрешность, что и метод
рядов Тейлора (6.7), однако является более
экономичным. Действительно, для расчета
нового значения функции здесь необходимо
2 раза вычислять значение функции
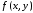 ,
в то время как в формуле (6.7) нам приходилось
для этих целей вычислять значения трех
функций. Кроме того, две из этих функций
являются производными функции
,
в то время как в формуле (6.7) нам приходилось
для этих целей вычислять значения трех
функций. Кроме того, две из этих функций
являются производными функции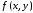 ,
требующими своего отыскания.
,
требующими своего отыскания.
