1.2 Этапы численного решения задач на эвм

Процесс численного решения задачи на ЭВМ состоит из следующих этапов:

1. постановка задачи;

2. разработка метода и алгоритма решения задачи;

3. написание компьютерной программы;

4. отладка программы;

5. проведение расчетов и анализ результатов.

Рассмотрим кратко содержание каждого этапа.

Постановка задачи заключается в построении математических зависимостей, адекватно описывающих техническую систему, т.е. в построении математической модели системы. Например, техническая система может быть описана системой линейных или нелинейных уравнений, дифференциальным уравнением и т.д.

Следующим этапом является разработка метода и алгоритма решения задачи. Дело в том, что многие задачи не могут быть решены в аналитическом виде. Поэтому существует необходимость разработки методов решения задачи в арифметической форме, требующей выполнения лишь арифметических операций сложения, вычитания, умножения, деления. Например, вычисление интеграла сводится к вычислению суммы, вычисление производной – к вычислению приращений функции и аргумента. Такие методы называются численными. Иногда разработанный численный метод представляют в виде алгоритма, т.е. в виде упорядоченной последовательности операций, позволяющих из исходных данных получить конечный результат.

Полученный алгоритм записывается на одном из алгоритмических языков в виде программы для решения на ЭВМ. Далее осуществляется отладка программы, во время которой выявляются допущенные в ней синтаксические ошибки, и проверяется правильность решения задачи на примерах с известным решением. После того как программа отлажена и есть уверенность, что она дает правильные результаты, выполняется большой объем расчетов по исследованию составленной модели.

1.3 Виды погрешностей решения задач

Любая задача не может быть решена абсолютно точно. Всегда будет существовать погрешность ее решения. Существуют 4 источника погрешности результата при решении любой задачи:

1. погрешность математической модели;

2. погрешность исходных данных;

3. погрешность численного метода;

4. погрешность округления.

Погрешность математической модели зависит от допущений при получении математической модели физического процесса. Например, чаще всего для простоты пытаются построить линейную модель. Для этого реальную зависимость заменяют линейной частью ряда Тейлора. При этом допускается определенная погрешность. Анализ погрешности математической модели относится к проблеме адекватности математической модели. В рамках данного пособия этот вопрос не рассматривается, т.е. всегда предполагается, что модель адекватна, и погрешность математической модели отсутствует.

Погрешность исходных данных появляется из-за неточности измерений, грубых недосмотров или невозможности представить исходные данные конечной десятичной дробью. Например, при использовании числа 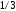в качестве исходного данного погрешность появится, если мы представим это число конечной десятичной дробью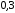или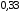. Часто случается, что дроби, которые являются конечными в одной системе счисления, становятся бесконечными в другой системе счисления. Например, конечная десятичная дробь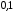, будучи переведенной в двоичную систему счисления, становится бесконечной дробью. 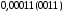Из-за конечности разрядной сетки ЭВМ мы не сможем удержать все двоичные цифры данного числа. Ошибки в исходных данных вызывают погрешность результата вычислений независимо от того, каким методом эти вычисления производятся. Поэтому погрешность результата, вызванная погрешностью исходных данных, называется неустранимой. В ряде случаев неустранимая погрешность может становиться недопустимо большой. Это происходит при решении так называемых некорректно поставленных задач. Задача называется некорректно поставленной (по А.Н. Тихонову), если небольшие погрешности в исходных данных приводят к большим погрешностям решения. В рамках данного пособия предполагается, что исходные данные могут содержать погрешности, однако все решаемые задачи являются корректно поставленными.

Погрешность численного метода связана с тем, что точные операторы заменяются приближенными, например, интеграл заменяется суммой, функция – многочленом, или строится бесконечный итерационный процесс, который обрывается после конечного числа итераций. Погрешность метода будем рассматривать для каждого численного метода. Численный метод необходимо подбирать таким образом, чтобы погрешность метода была в 2 – 5 раз меньше погрешности исходных данных. Очень большая погрешность метода снижает точность ответа, а очень малая невыгодна, так как обычно требует значительного увеличения объема вычислений.

Погрешность округления связана с округлением чисел, участвующих в операциях, поскольку числа в памяти ЭВМ хранятся с удержанием лишь конечного числа их значащих цифр.