- •Теоретический раздел Предисловие
- •Предисловие ко второму изданию
- •1 Математические модели. Численные методы. Погрешности вычислений
- •1.1 Математические модели и моделирование
- •1.2 Этапы численного решения задач на эвм
- •1.3 Виды погрешностей решения задач
- •1.4 Погрешности арифметических операций
- •1.5 Графы арифметических операций
- •1.6 Распространение погрешностей в вычислениях
- •2 Решение систем линейных алгебраических уравнений
- •2.1 Постановка задачи. Методы решения
- •2.2 Метод Гаусса
- •2.2.1 Описание метода Гаусса
- •2.2.2 Расчетные формулы метода Гаусса
- •2.2.3 Погрешность метода Гаусса. Метод Гаусса с выбором главного элемента
- •2.3 Вычислительная сложность метода Гаусса
- •2.4 Обращение матрицы
- •2.5 Метод lu-разложения
- •2.6 Метод квадратного корня решения симметричных слау
- •2.7 Метод Гаусса–Зейделя
- •2.7.1 Расчетные формулы метода Гаусса–Зейделя
- •2.7.2 Сходимость метода Гаусса–Зейделя
- •2.7.3 Графическая иллюстрация метода Гаусса–Зейделя
- •3 Аппроксимация функций
- •3.1 Понятие аппроксимации функций
- •3.2 Постановка задачи интерполирования функций
- •3.3 Интерполяционный полином Лагранжа
- •3.4 Вычисление значений полиномов
- •3.5 Вычислительная сложность задачи интерполирования
- •3.6 Конечные и разделенные разности функции
- •3.7 Интерполяционный полином Ньютона
- •3.8 Погрешность интерполирования
- •3.9 Полиномы Чебышева 1-го рода
- •3.10 Наилучший выбор узлов интерполирования
- •4 Численное интегрирование
- •4.1 Постановка задачи численного интегрирования
- •4.2 Метод прямоугольников
- •4.3 Погрешность метода прямоугольников
- •4.4 Метод трапеций
- •4.5 Погрешность метода трапеций
- •4.6 Метод Симпсона
- •4.7 Погрешность метода Симпсона
- •4.8 Интерполяционные квадратурные формулы
- •4.9 Интерполяционные квадратурные формулы наивысшей алгебраической степени точности (квадратурные формулы Гаусса)
- •4.9.1 Квадратурная формула Гаусса–Лежандра
- •4.9.2 Квадратурная формула Гаусса–Лагерра
- •4.9.3 Квадратурная формула Гаусса–Эрмита
- •5 Решение нелинейных уравнений
- •5.1 Постановка задачи численного решения нелинейных уравнений
- •5.2 Метод деления отрезка пополам
- •5.3 Метод хорд
- •5.4 Метод простой итерации
- •5.5 Метод Ньютона
- •5.6 Метод секущих
- •6 Решение обыкновенных дифференциальных уравнений
- •6.1 Постановка задачи
- •6.2 Метод рядов Тейлора
- •6.3 Метод Эйлера
- •6.4 Метод Рунге–Кутта 2-го порядка
- •6.5 Метод Рунге–Кутта 4-го порядка
- •7 Решение систем обыкновенных дифференциальных уравнений
- •7.1 Постановка задачи
- •7.2 Приведение дифференциального уравнения -го порядка к системе дифференциальных уравнений 1-го порядка
- •7.3 Метод Эйлера
- •8.2 Выполнение символьных операций в Matlab
- •8.3 Создание символьных переменных
- •8.4 Создание группы символьных переменных
- •8.5 Создание списка символьных переменных
- •8.6 Вывод символьного выражения
- •8.7 Упрощение выражений
- •8.8 Вычисление производных
- •8.9 Вычисление интегралов
- •8.10 Вычисление сумм рядов
- •8.11 Вычисление пределов
- •8.12 Разложение функции в ряд Тейлора
- •8.13 Вычисление определителя матрицы, обращение матрицы
- •9 Дополнение
- •9.1 Вычисление корней полиномов
- •9.2 Решение систем нелинейных уравнений. Метод Ньютона
- •9.3 Решение систем линейных алгебраических уравнений с трехдиагональной матрицей (метод прогонки)
- •9.4 Интерполирование функций сплайнами
- •Практический раздел Указания к выбору варианта
- •Лабораторная работа № 1. Работа в системе Matlab
- •1.1. Цель работы
- •1.2. Порядок выполнения работы
- •Лабораторная работа № 2. Решение систем линейных алгебраических уравнений
- •2.1. Цель работы
- •2.2. Теоретические положения
- •2.3. Порядок выполнения работы
- •Лабораторная работа № 3. Аппроксимация функций
- •3.1. Цель работы
- •3.2. Теоретические положения
- •3.3. Порядок выполнения работы
- •Лабораторная работа № 4. Численное интегрирование
- •4.1. Цель работы
- •4.2. Теоретические положения
- •4.3. Порядок выполнения работы
- •Лабораторная работа № 5. Решение нелинейных уравнений
- •5.1. Цель работы
- •5.2. Теоретические положения
- •5.3. Порядок выполнения работы
- •Лабораторная работа № 6. Решение обыкновенных дифференциальных уравнений
- •6.1. Цель работы
- •6.2. Теоретические положения
- •6.3. Порядок выполнения работы
- •Лабораторная работа № 7. Решение систем обыкновенных дифференциальных уравнений
- •7.1. Цель работы
- •7.2. Теоретические положения
- •7.3. Порядок выполнения работы
- •Лабораторная работа № 8. Выполнение символьных операций
- •8.1. Цель работы
- •8.2. Теоретические сведения
- •8.3. Порядок выполнения работы
- •Литература
- •Литература
3.7 Интерполяционный полином Ньютона
Пусть
в точках
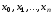 отрезка
отрезка известны значения
известны значения функции
функции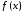 .
Построим по этим данным интерполяционный
полином
.
Построим по этим данным интерполяционный
полином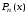 в форме полинома Ньютона. Построение
основывается на том, что разделенные
разности интерполяционного полинома
и функции совпадают, т.е.
в форме полинома Ньютона. Построение
основывается на том, что разделенные
разности интерполяционного полинома
и функции совпадают, т.е.
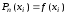 ,
,
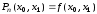 ,
,
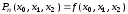 ,
(3.18)
,
(3.18)
……………………………..
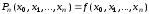 .
.
Кроме того, мы знаем, что
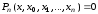 .
(3.19)
.
(3.19)
Запишем
разделенную разность первого порядка
для полинома
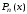 :
:
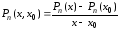 .
.
Отсюда
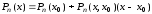 .
(3.20)
.
(3.20)
Разделенная разность произвольного порядка имеет вид
 ,
,
откуда
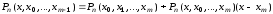 .
.
Последняя
формула позволяет перейти от разделенной
разности
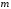 -го
порядка к разделенной разности более
высокого
-го
порядка к разделенной разности более
высокого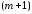 -го
порядка. В частности,
-го
порядка. В частности,
 ,
,
 .
.
Используя эти формулы, из формулы (3.20) последовательно получаем
 ,
,
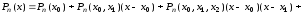
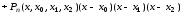 .
.
Продолжая этот процесс, в итоге получим формулу
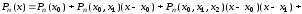
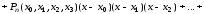

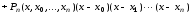 .
.
Учитывая
равенства (3.18), (3.19), получаем полином
Ньютона для неравноотстоящих узлов,
выраженный через разделенные разности
в начальной точке
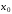 :
:
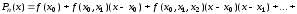
 .
(3.21)
.
(3.21)
Отметим,
что при выводе формулы полинома Ньютона
мы не предполагали, что узлы располагаются
в порядке возрастания. Поэтому порядок
узлов в выражении полинома Ньютона
можно изменять. Изменив порядок узлов
на обратный, мы получим следующее
выражение полинома Ньютона, записанное
через разделенные разности в конечной
точке
 :
:

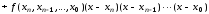 .
(3.22)
.
(3.22)
Если
точки
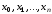 отстоят одна от другой на равном
расстоянии
отстоят одна от другой на равном
расстоянии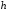 ,
то с учетом равенства (3.17) получаем
полином Ньютона, выраженный через
конечные разности в начальной точке
,
то с учетом равенства (3.17) получаем
полином Ньютона, выраженный через
конечные разности в начальной точке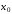 :
:

 .
(3.23)
.
(3.23)
Аналогичным
образом получаем полином Ньютона,
выраженный через конечные разности в
конечной точке
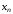 :
:
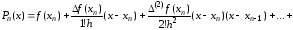
 .
(3.24)
.
(3.24)
Полиномы Ньютона удобны тогда, когда необходимо изменять количество узлов интерполирования. При увеличении количества узлов нет необходимости пересчитывать весь полином, достаточно прибавить к нему новые слагаемые, соответствующие новым узлам. В случае полинома Лагранжа при добавлении новых узлов приходится пересчитывать весь полином.
Полиномы
(3.21), (3.23), полученные по разностям в
начальной точке
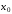 ,
используются для интерполирования
функции вблизи начальной точки
,
используются для интерполирования
функции вблизи начальной точки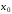 ,
а полиномы (3.22), (3.24), полученные по
разностям в конечной точке
,
а полиномы (3.22), (3.24), полученные по
разностям в конечной точке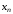 ,
– для интерполирования вблизи конечной
точки
,
– для интерполирования вблизи конечной
точки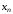 .
.
Пример 3.2. Построим интерполяционный полином Ньютона по данным примера 3.1 п. 3.3. Для этого по таблице 3.1 составим таблицу разделенных разностей (таблица 3.2).
Таблица 3.2
|
|
|
|
|
|
-2 |
12 |
|
|
|
|
|
-6 |
|
|
-1 |
6 |
|
1 |
|
|
|
-1 |
|
|
3 |
2 |
|
|
Разделенные
разности образуют верхнюю убывающую
диагональ, содержащую разделенные
разности в начальной точке
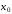 (числа 12, -6, 1), и нижнюю возрастающую
диагональ, содержащую разделенные
разности в конечной точке
(числа 12, -6, 1), и нижнюю возрастающую
диагональ, содержащую разделенные
разности в конечной точке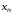 (числа 2, -1, 1). Используя разделенные
разности в начальной точке
(числа 2, -1, 1). Используя разделенные
разности в начальной точке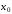 ,
получаем полином Ньютона
,
получаем полином Ньютона
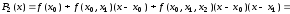
 .
.
Используя
разделенные разности в конечной точке
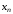 ,
получаем полином
,
получаем полином
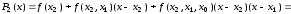
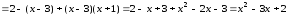 .
.
В обоих случаях мы получили один и тот же полином, совпадающий с полиномом Лагранжа в примере 3.1.