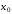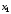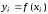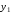- •Теоретический раздел Предисловие
- •Предисловие ко второму изданию
- •1 Математические модели. Численные методы. Погрешности вычислений
- •1.1 Математические модели и моделирование
- •1.2 Этапы численного решения задач на эвм
- •1.3 Виды погрешностей решения задач
- •1.4 Погрешности арифметических операций
- •1.5 Графы арифметических операций
- •1.6 Распространение погрешностей в вычислениях
- •2 Решение систем линейных алгебраических уравнений
- •2.1 Постановка задачи. Методы решения
- •2.2 Метод Гаусса
- •2.2.1 Описание метода Гаусса
- •2.2.2 Расчетные формулы метода Гаусса
- •2.2.3 Погрешность метода Гаусса. Метод Гаусса с выбором главного элемента
- •2.3 Вычислительная сложность метода Гаусса
- •2.4 Обращение матрицы
- •2.5 Метод lu-разложения
- •2.6 Метод квадратного корня решения симметричных слау
- •2.7 Метод Гаусса–Зейделя
- •2.7.1 Расчетные формулы метода Гаусса–Зейделя
- •2.7.2 Сходимость метода Гаусса–Зейделя
- •2.7.3 Графическая иллюстрация метода Гаусса–Зейделя
- •3 Аппроксимация функций
- •3.1 Понятие аппроксимации функций
- •3.2 Постановка задачи интерполирования функций
- •3.3 Интерполяционный полином Лагранжа
- •3.4 Вычисление значений полиномов
- •3.5 Вычислительная сложность задачи интерполирования
- •3.6 Конечные и разделенные разности функции
- •3.7 Интерполяционный полином Ньютона
- •3.8 Погрешность интерполирования
- •3.9 Полиномы Чебышева 1-го рода
- •3.10 Наилучший выбор узлов интерполирования
- •4 Численное интегрирование
- •4.1 Постановка задачи численного интегрирования
- •4.2 Метод прямоугольников
- •4.3 Погрешность метода прямоугольников
- •4.4 Метод трапеций
- •4.5 Погрешность метода трапеций
- •4.6 Метод Симпсона
- •4.7 Погрешность метода Симпсона
- •4.8 Интерполяционные квадратурные формулы
- •4.9 Интерполяционные квадратурные формулы наивысшей алгебраической степени точности (квадратурные формулы Гаусса)
- •4.9.1 Квадратурная формула Гаусса–Лежандра
- •4.9.2 Квадратурная формула Гаусса–Лагерра
- •4.9.3 Квадратурная формула Гаусса–Эрмита
- •5 Решение нелинейных уравнений
- •5.1 Постановка задачи численного решения нелинейных уравнений
- •5.2 Метод деления отрезка пополам
- •5.3 Метод хорд
- •5.4 Метод простой итерации
- •5.5 Метод Ньютона
- •5.6 Метод секущих
- •6 Решение обыкновенных дифференциальных уравнений
- •6.1 Постановка задачи
- •6.2 Метод рядов Тейлора
- •6.3 Метод Эйлера
- •6.4 Метод Рунге–Кутта 2-го порядка
- •6.5 Метод Рунге–Кутта 4-го порядка
- •7 Решение систем обыкновенных дифференциальных уравнений
- •7.1 Постановка задачи
- •7.2 Приведение дифференциального уравнения -го порядка к системе дифференциальных уравнений 1-го порядка
- •7.3 Метод Эйлера
- •8.2 Выполнение символьных операций в Matlab
- •8.3 Создание символьных переменных
- •8.4 Создание группы символьных переменных
- •8.5 Создание списка символьных переменных
- •8.6 Вывод символьного выражения
- •8.7 Упрощение выражений
- •8.8 Вычисление производных
- •8.9 Вычисление интегралов
- •8.10 Вычисление сумм рядов
- •8.11 Вычисление пределов
- •8.12 Разложение функции в ряд Тейлора
- •8.13 Вычисление определителя матрицы, обращение матрицы
- •9 Дополнение
- •9.1 Вычисление корней полиномов
- •9.2 Решение систем нелинейных уравнений. Метод Ньютона
- •9.3 Решение систем линейных алгебраических уравнений с трехдиагональной матрицей (метод прогонки)
- •9.4 Интерполирование функций сплайнами
- •Практический раздел Указания к выбору варианта
- •Лабораторная работа № 1. Работа в системе Matlab
- •1.1. Цель работы
- •1.2. Порядок выполнения работы
- •Лабораторная работа № 2. Решение систем линейных алгебраических уравнений
- •2.1. Цель работы
- •2.2. Теоретические положения
- •2.3. Порядок выполнения работы
- •Лабораторная работа № 3. Аппроксимация функций
- •3.1. Цель работы
- •3.2. Теоретические положения
- •3.3. Порядок выполнения работы
- •Лабораторная работа № 4. Численное интегрирование
- •4.1. Цель работы
- •4.2. Теоретические положения
- •4.3. Порядок выполнения работы
- •Лабораторная работа № 5. Решение нелинейных уравнений
- •5.1. Цель работы
- •5.2. Теоретические положения
- •5.3. Порядок выполнения работы
- •Лабораторная работа № 6. Решение обыкновенных дифференциальных уравнений
- •6.1. Цель работы
- •6.2. Теоретические положения
- •6.3. Порядок выполнения работы
- •Лабораторная работа № 7. Решение систем обыкновенных дифференциальных уравнений
- •7.1. Цель работы
- •7.2. Теоретические положения
- •7.3. Порядок выполнения работы
- •Лабораторная работа № 8. Выполнение символьных операций
- •8.1. Цель работы
- •8.2. Теоретические сведения
- •8.3. Порядок выполнения работы
- •Литература
- •Литература
Лабораторная работа № 3. Аппроксимация функций
3.1. Цель работы
3.1.1. Ознакомление с задачей аппроксимации функций одной переменной, изучение задачи интерполирования функций.
3.1.2. Приобретение навыков программирования интерполяционных формул.
3.1.3. Приобретение навыков использования стандартных средств системы Matlab для интерполирования функций.
3.2. Теоретические положения
3.2.1. Понятие аппроксимации функций
Аппроксимация
функции
 – это замена этой функции другой более
простой функцией
– это замена этой функции другой более
простой функцией ,
близкой к
,
близкой к в некотором смысле. Критерий близости
функций
в некотором смысле. Критерий близости
функций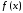 и
и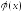 определяет способ аппроксимации.
определяет способ аппроксимации.
Если
расстояние
 между функциями
между функциями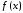 и
и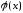 на некотором отрезке
на некотором отрезке действительной прямой определить
выражением
действительной прямой определить
выражением
 ,
,
то
аппроксимация функции
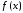 по критерию минимума такого расстояния
по критерию минимума такого расстояния будет называться аппроксимацией с
минимальной интегральной квадратичной
погрешностью.
будет называться аппроксимацией с
минимальной интегральной квадратичной
погрешностью.
Если
критерий близости функций
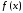 и
и состоит в том, чтобы
состоит в том, чтобы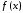 и
и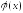 совпадали в дискретном ряде точек
совпадали в дискретном ряде точек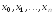 отрезка
отрезка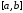 ,
то такой способ аппроксимации функции
,
то такой способ аппроксимации функции называетсяинтерполированием
функции
называетсяинтерполированием
функции
 .
.
Если
расстояние
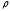 между функциями
между функциями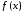 и
и на некотором отрезке
на некотором отрезке действительной прямой определить
выражением
действительной прямой определить
выражением
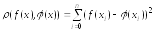 ,
,
то
аппроксимация функции
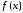 по критерию минимума такого расстояния
по критерию минимума такого расстояния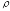 будет называться аппроксимацией по
методу наименьших квадратов.
будет называться аппроксимацией по
методу наименьших квадратов.
3.2.2. Постановка задачи интерполирования функций
Задача
интерполирования функции
 на некотором отрезке
на некотором отрезке формулируется следующим образом. На
отрезке
формулируется следующим образом. На
отрезке задано
задано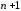 точек
точек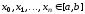 ,
которые называют узлами. Обычно считают,
что первая и последняя точки совпадают
с концами отрезка
,
которые называют узлами. Обычно считают,
что первая и последняя точки совпадают
с концами отрезка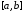 :
: ,
,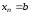 .
Известны значения
.
Известны значения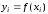 функции
функции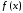 в этих точках,
в этих точках,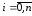 .
Требуется заменить эту функцию некоторой
другой функцией
.
Требуется заменить эту функцию некоторой
другой функцией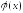 таким образом, чтобы значения обеих
функций совпадали в узлах, т.е. чтобы
выполнялись равенства
таким образом, чтобы значения обеих
функций совпадали в узлах, т.е. чтобы
выполнялись равенства
 .
.
Искомой
неизвестной в данной задаче является
функция
 .
.
Сформулированную
задачу иногда интерпретируют следующим
образом. Некоторая функция
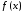 задана на отрезке
задана на отрезке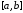 таблицей
своих значений
таблицей
своих значений
|
|
|
|
|
… |
|
|
|
|
|
|
… |
|
и
требуется найти способ определения
значений этой функции в любых других
точках отрезка
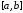 .
.
При
формулировке задачи интерполирования
обычно предполагают, что аппроксимирующая
функция
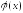 задана с точностью до
задана с точностью до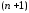 параметров
параметров ,
т.е. в виде
,
т.е. в виде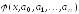 .
Тогда нам необходимо отыскатьнеизвестные
параметры
.
Тогда нам необходимо отыскатьнеизвестные
параметры
 исходя из заданных равенств
исходя из заданных равенств
 .
(3.1)
.
(3.1)
Эти
равенства можно рассматривать как
систему
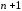 уравнений относительно неизвестных
коэффициентов
уравнений относительно неизвестных
коэффициентов .
.
Чаще
всего функцию
 представляют в виде полинома
представляют в виде полинома
 -й
степени
-й
степени
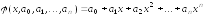 .
(3.2)
.
(3.2)
Тогда система уравнений (3.1) принимает следующий вид:
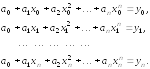 (3.3)
(3.3)
Определитель этой системы имеет вид
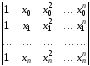
и
называется определителем Вандермонда
на системе точек
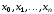 .
Доказано, что если точки
.
Доказано, что если точки попарно различны, что предполагается
при постановке задачи, то определитель
Вандермонда не равен нулю. Тогда система
уравнений (3.3) имеет единственное решение,
т.е. существует единственный полином
(3.2) степени
попарно различны, что предполагается
при постановке задачи, то определитель
Вандермонда не равен нулю. Тогда система
уравнений (3.3) имеет единственное решение,
т.е. существует единственный полином
(3.2) степени ,
коэффициенты которого удовлетворяют
системе уравнений (3.3). Этот полином
называется интерполяционным полиномом
для функции
,
коэффициенты которого удовлетворяют
системе уравнений (3.3). Этот полином
называется интерполяционным полиномом
для функции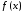 .
.
3.2.3. Интерполяционный полином Лагранжа
Интерполяционный полином может быть представлен в различных формах. Одной из них является форма Лагранжа. Полином Лагранжа имеет следующий вид:
 ,
,
или в компактной форме
 .
(3.4)
.
(3.4)
Этот
полином легко может быть получен путем
следующих рассуждений. Рассмотрим так
называемый полином влияния
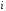 -го
узла:
-го
узла:

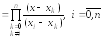 .
(3.5)
.
(3.5)
Понятно,
что это полином
 -й
степени. Из выражения (3.5)
видно, что он равен нулю в любых точках,
кроме
-й
степени. Из выражения (3.5)
видно, что он равен нулю в любых точках,
кроме
 ,
а в точке
,
а в точке равен 1. Вид этого полинома приведен на
рис. 3.1. Произведение
равен 1. Вид этого полинома приведен на
рис. 3.1. Произведение есть полином
есть полином -й
степени, который во всех узлах, кроме
-й
степени, который во всех узлах, кроме ,
равен нулю, а в узле
,
равен нулю, а в узле равен
равен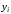 .
Просуммировав произведения
.
Просуммировав произведения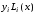 по всем
по всем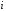 (по всем узлам ), мы получим полином
(3.4),
удовлетворяющий постановке задачи
интерполирования. Следовательно,
построенный полином будет интерполяционным.
(по всем узлам ), мы получим полином
(3.4),
удовлетворяющий постановке задачи
интерполирования. Следовательно,
построенный полином будет интерполяционным.

Рис. 3.1.
Полином Лагранжа можно записать в другом виде. Для этого рассмотрим полином
 .
(3.6)
.
(3.6)
Это
полином
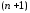 -й
степени со старшим коэффициентом, равным
1, и обращающийся в нуль во всех узлах.
Легко показать, что производная от этого
полинома в точке
-й
степени со старшим коэффициентом, равным
1, и обращающийся в нуль во всех узлах.
Легко показать, что производная от этого
полинома в точке имеет вид
имеет вид
 .
.
Тогда
полином влияния
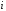 -го
узла (3.5) можно записать в виде
-го
узла (3.5) можно записать в виде
 ,
,
а сам полином Лагранжа (3.4) – в виде
 .
(3.7)
.
(3.7)
3.2.4. Погрешность интерполирования
Погрешность интерполяционного полинома Лагранжа оценивается выражением
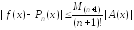 ,
,
где
 – максимальное по модулю значение
– максимальное по модулю значение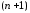 -й
производной функции
-й
производной функции на отрезке интерполирования
на отрезке интерполирования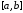 ,
, – полином (3.6).
– полином (3.6).
3.2.5. Наилучший выбор узлов интерполирования
Чаще
всего узлы интерполирования располагают
на отрезке интерполирования с равномерным
шагом. Вместе с тем, выбирая неравномерную
сетку узлов, можно увеличить точность
интерполирования. Задача о наилучшем
выборе узлов интерполирования была
решена Чебышевым. Наилучшие узлы
интерполирования выбираются равными
корням так называемого "полинома,
наименее отклоняющегося от нуля" на
отрезке интерполирования
 .
Полином, наименее отклоняющийся от нуля
на отрезке
.
Полином, наименее отклоняющийся от нуля
на отрезке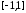 ,
был найден Чебышевым и назван его
именем. Полином Чебышева
,
был найден Чебышевым и назван его
именем. Полином Чебышева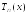 определяется следующим выражением:
определяется следующим выражением:
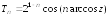 .
.
Следовательно,
наилучшие узлы интерполирования
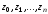 на отрезке
на отрезке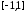 выбираются из условия
выбираются из условия

и имеют следующие значения:
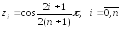 .
(3.8)
.
(3.8)
Наилучшие
узлы интерполирования на произвольном
отрезке
 находятся по формуле
находятся по формуле
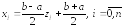 ,
(3.9)
,
(3.9)
где
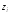 – узлы (3.8).
– узлы (3.8).
3.2.6. Средства Matlab для интерполирования функций
Для интерполирования функций в Matlab можно использовать функции polyfit и polyval.
Функция
a=polyfit(x,
y,
n)
находит массив коэффициентов
 длиной
длиной полинома степени
полинома степени по массивам длиной
по массивам длиной узлов
узлов и значений функции в узлах
и значений функции в узлах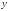 ,
,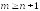 .
Этот полином аппроксимирует функцию
.
Этот полином аппроксимирует функцию по методу наименьших квадратов.
Предполагается, что полином задается
в виде
по методу наименьших квадратов.
Предполагается, что полином задается
в виде
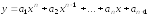 .
.
Если
 ,
то программа возвращает коэффициенты
интерполяционного полинома.
,
то программа возвращает коэффициенты
интерполяционного полинома.
Функция
y=polyval(a,x)
возвращает значение
 полинома в точке
полинома в точке ,
коэффициенты которого определены в
векторе
,
коэффициенты которого определены в
векторе .
.
Таким образом, для интерполирования функции необходимо последовательно обратиться к функциям polyfit и polyval.