3.10 Наилучший выбор узлов интерполирования

Из формулы (3.27) видно, что погрешность интерполирования зависит от двух множителей, один из которых 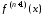зависит от свойств интерполируемой функции и не поддается регулированию, а величина другого 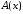определяется исключительно выбором узлов интерполирования. Чаще всего узлы интерполирования располагают на отрезке интерполирования с равномерным шагом. Вместе с тем, выбирая неравномерную сетку узлов, можно увеличить точность интерполирования. Задача о наилучшем выборе узлов интерполирования была сформулирована и решена русским математиком П. Л. Чебышевым. Наилучшие узлы интерполирования выбираются равными корням полинома, наименее уклоняющегося от нуля на отрезке интерполирования. Действительно, полином-й степени, наименее уклоняющийся от нуля на отрезке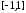, – это нормированный полином Чебышева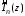(3.30), допускающий представление (3.31). Выполним линейное преобразование независимой переменной:

.

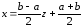Это преобразование осуществляет взаимно-однозначное соответствие между и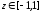. Благодаря этому преобразованию каждому узлу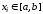можно сопоставить точкупо формуле

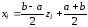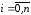, , (3.33)

в результате чего образующие полином 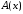сомножители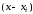в формуле для погрешности интерполирования (3.28) преобразуются по формуле

.

Следовательно,

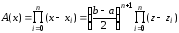. (3.34)

Из последней формулы видно, что значение будет минимальным, когда будет минимальным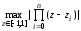. Так как коэффициент при старшей степени полиномаравен 1, то на основании представления (3.31) это есть нормированный полином Чебышева 1-го рода, а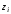– его корни.

Итак, наилучшие узлы интерполирования 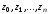на отрезке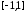выбираются из условия

,

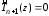т.е. как решение уравнения

.

Из этого уравнения получаем:

, ,

,

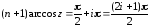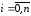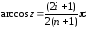так что наилучшие узлы интерполирования определяются формулой

, .

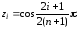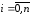Наилучшие узлы интерполирования на произвольном отрезке 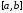находятся по формуле (3.33).

Подчеркнем, что при таком выборе узлов мы сводим к минимуму максимальное значение погрешности интерполирования. Найдем это максимальное значение погрешности интерполирования в случае наилучшего выбора узлов интерполирования. Учитывая выражение (3.32) и формулу (3.34), получим

.

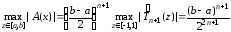В итоге из формулы (3.28) для погрешности интерполирования при наилучшем выборе узлов будем иметь соотношение

.

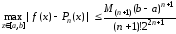4 Численное интегрирование

4.1 Постановка задачи численного интегрирования

Задача численного интегрирования состоит в том, чтобы найти численное значение определенного интеграла

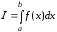, (4.1)

где 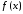– функция, непрерывная на отрезке интегрирования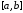. Формулы для решения этой задачи называются квадратурными. Квадратурная формула позволяет вместо точного значения интеграла (4.1) найти некоторое его приближенное значение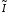. Разность точного и приближенного значений интеграла называется абсолютной погрешностью квадратурной формулы (или численного метода),

.

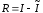Квадратурные формулы используют для вычисления интеграла (4.1) значения 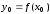,,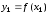…,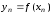функции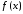в точкахотрезка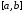. Квадратурная формула имеет вид

,

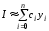где 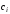– некоторые коэффициенты, которые называются весовыми. Рассмотрим различные квадратурные формулы и их погрешности.