
- •Теоретический раздел Предисловие
- •Предисловие ко второму изданию
- •1 Математические модели. Численные методы. Погрешности вычислений
- •1.1 Математические модели и моделирование
- •1.2 Этапы численного решения задач на эвм
- •1.3 Виды погрешностей решения задач
- •1.4 Погрешности арифметических операций
- •1.5 Графы арифметических операций
- •1.6 Распространение погрешностей в вычислениях
- •2 Решение систем линейных алгебраических уравнений
- •2.1 Постановка задачи. Методы решения
- •2.2 Метод Гаусса
- •2.2.1 Описание метода Гаусса
- •2.2.2 Расчетные формулы метода Гаусса
- •2.2.3 Погрешность метода Гаусса. Метод Гаусса с выбором главного элемента
- •2.3 Вычислительная сложность метода Гаусса
- •2.4 Обращение матрицы
- •2.5 Метод lu-разложения
- •2.6 Метод квадратного корня решения симметричных слау
- •2.7 Метод Гаусса–Зейделя
- •2.7.1 Расчетные формулы метода Гаусса–Зейделя
- •2.7.2 Сходимость метода Гаусса–Зейделя
- •2.7.3 Графическая иллюстрация метода Гаусса–Зейделя
- •3 Аппроксимация функций
- •3.1 Понятие аппроксимации функций
- •3.2 Постановка задачи интерполирования функций
- •3.3 Интерполяционный полином Лагранжа
- •3.4 Вычисление значений полиномов
- •3.5 Вычислительная сложность задачи интерполирования
- •3.6 Конечные и разделенные разности функции
- •3.7 Интерполяционный полином Ньютона
- •3.8 Погрешность интерполирования
- •3.9 Полиномы Чебышева 1-го рода
- •3.10 Наилучший выбор узлов интерполирования
- •4 Численное интегрирование
- •4.1 Постановка задачи численного интегрирования
- •4.2 Метод прямоугольников
- •4.3 Погрешность метода прямоугольников
- •4.4 Метод трапеций
- •4.5 Погрешность метода трапеций
- •4.6 Метод Симпсона
- •4.7 Погрешность метода Симпсона
- •4.8 Интерполяционные квадратурные формулы
- •4.9 Интерполяционные квадратурные формулы наивысшей алгебраической степени точности (квадратурные формулы Гаусса)
- •4.9.1 Квадратурная формула Гаусса–Лежандра
- •4.9.2 Квадратурная формула Гаусса–Лагерра
- •4.9.3 Квадратурная формула Гаусса–Эрмита
- •5 Решение нелинейных уравнений
- •5.1 Постановка задачи численного решения нелинейных уравнений
- •5.2 Метод деления отрезка пополам
- •5.3 Метод хорд
- •5.4 Метод простой итерации
- •5.5 Метод Ньютона
- •5.6 Метод секущих
- •6 Решение обыкновенных дифференциальных уравнений
- •6.1 Постановка задачи
- •6.2 Метод рядов Тейлора
- •6.3 Метод Эйлера
- •6.4 Метод Рунге–Кутта 2-го порядка
- •6.5 Метод Рунге–Кутта 4-го порядка
- •7 Решение систем обыкновенных дифференциальных уравнений
- •7.1 Постановка задачи
- •7.2 Приведение дифференциального уравнения -го порядка к системе дифференциальных уравнений 1-го порядка
- •7.3 Метод Эйлера
- •8.2 Выполнение символьных операций в Matlab
- •8.3 Создание символьных переменных
- •8.4 Создание группы символьных переменных
- •8.5 Создание списка символьных переменных
- •8.6 Вывод символьного выражения
- •8.7 Упрощение выражений
- •8.8 Вычисление производных
- •8.9 Вычисление интегралов
- •8.10 Вычисление сумм рядов
- •8.11 Вычисление пределов
- •8.12 Разложение функции в ряд Тейлора
- •8.13 Вычисление определителя матрицы, обращение матрицы
- •9 Дополнение
- •9.1 Вычисление корней полиномов
- •9.2 Решение систем нелинейных уравнений. Метод Ньютона
- •9.3 Решение систем линейных алгебраических уравнений с трехдиагональной матрицей (метод прогонки)
- •9.4 Интерполирование функций сплайнами
- •Практический раздел Указания к выбору варианта
- •Лабораторная работа № 1. Работа в системе Matlab
- •1.1. Цель работы
- •1.2. Порядок выполнения работы
- •Лабораторная работа № 2. Решение систем линейных алгебраических уравнений
- •2.1. Цель работы
- •2.2. Теоретические положения
- •2.3. Порядок выполнения работы
- •Лабораторная работа № 3. Аппроксимация функций
- •3.1. Цель работы
- •3.2. Теоретические положения
- •3.3. Порядок выполнения работы
- •Лабораторная работа № 4. Численное интегрирование
- •4.1. Цель работы
- •4.2. Теоретические положения
- •4.3. Порядок выполнения работы
- •Лабораторная работа № 5. Решение нелинейных уравнений
- •5.1. Цель работы
- •5.2. Теоретические положения
- •5.3. Порядок выполнения работы
- •Лабораторная работа № 6. Решение обыкновенных дифференциальных уравнений
- •6.1. Цель работы
- •6.2. Теоретические положения
- •6.3. Порядок выполнения работы
- •Лабораторная работа № 7. Решение систем обыкновенных дифференциальных уравнений
- •7.1. Цель работы
- •7.2. Теоретические положения
- •7.3. Порядок выполнения работы
- •Лабораторная работа № 8. Выполнение символьных операций
- •8.1. Цель работы
- •8.2. Теоретические сведения
- •8.3. Порядок выполнения работы
- •Литература
- •Литература
3.8 Погрешность интерполирования
Абсолютная
погрешность интерполяционного полинома
Лагранжа – это разность
 ,
где
,
где
 – интерполируемая функция,
– интерполируемая функция,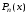 – интерполяционный полином Лагранжа.
Поскольку абсолютная погрешность
интерполирования равна нулю в узлах
интерполирования, то ее можно представить
в виде
– интерполяционный полином Лагранжа.
Поскольку абсолютная погрешность
интерполирования равна нулю в узлах
интерполирования, то ее можно представить
в виде
 ,
(3.25)
,
(3.25)
где
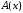 – полином (3.5). Будем считать, что на
отрезке интерполирования
– полином (3.5). Будем считать, что на
отрезке интерполирования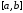 функция
функция имеет производные до
имеет производные до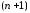 -го
порядка включительно. Введем вспомогательную
функцию
-го
порядка включительно. Введем вспомогательную
функцию
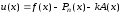 .
(3.26)
.
(3.26)
Функция
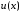 ,
очевидно, имеет
,
очевидно, имеет корень в точках
корень в точках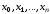 .
Подберем коэффициент
.
Подберем коэффициент в выражении (3.26) так, чтобы
в выражении (3.26) так, чтобы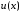 имела
имела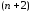 -й
корень в некоторой точке
-й
корень в некоторой точке отрезка
отрезка ,
не совпадающей с узлами интерполирования.
Для этого достаточно положить
,
не совпадающей с узлами интерполирования.
Для этого достаточно положить
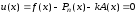 .
.
Так
как в предполагаемой точке

 ,
то этот коэффициент вполне определяется
последним уравнением. При таком значении
коэффициента
,
то этот коэффициент вполне определяется
последним уравнением. При таком значении
коэффициента функция
функция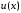 имеет
имеет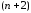 корня на отрезке
корня на отрезке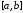 и обращается в нуль на концах каждого
из следующих
и обращается в нуль на концах каждого
из следующих отрезков:
отрезков: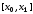 ,
,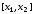 ,…,
,…, ,
,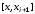 ,…,
,…,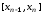 .
Применяя к каждому из этих отрезков
теорему Ролля1,
убеждаемся, что производная
.
Применяя к каждому из этих отрезков
теорему Ролля1,
убеждаемся, что производная не менее
не менее раза обращается в нуль на
раза обращается в нуль на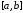 .
Применяя теорему Ролля к производной
.
Применяя теорему Ролля к производной ,
убеждаемся, что вторая производная
,
убеждаемся, что вторая производная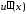 не менее
не менее раз обращается в нуль на
раз обращается в нуль на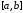 .
Продолжая эти рассуждения, приходим к
заключению, что производная
.
Продолжая эти рассуждения, приходим к
заключению, что производная хотя бы 1 раз обращается в нуль на
хотя бы 1 раз обращается в нуль на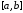 .
Это значит, что существует точка
.
Это значит, что существует точка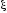 ,
для которой
,
для которой
 .
.
Из формулы (3.26) получаем
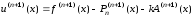 .
.
Так как производные
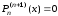 ,
,
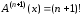 ,
,
то
 ,
,
а
в точке


Отсюда
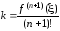 ,
,
и из выражения (3.25) получим следующую формулу для абсолютной погрешности интерполяционного полинома Лагранжа:
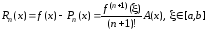 .
(3.27)
.
(3.27)
Из последнего выражения получаем оценку абсолютной погрешности интерполирования в виде
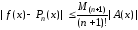 ,
(3.28)
,
(3.28)
где
![]() – максимальное по модулю значение
– максимальное по модулю значение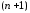 -й
производной функции
-й
производной функции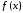 на отрезке интерполирования
на отрезке интерполирования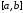 .
.
3.9 Полиномы Чебышева 1-го рода
Полиномы Чебышева 1-го рода встречаются в задаче наилучшего выбора узлов интерполирования, рассмотренной далее в п. 3.10.
Рассмотрим
следующую задачу: среди всех полиномов
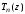 степени
степени со старшим коэффициентом, равным единице,
найти такой, для которого величина
со старшим коэффициентом, равным единице,
найти такой, для которого величина
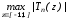
является
минимальной. Такой полином называется
полиномом, наименее уклоняющимся от
нуля на отрезке
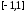 .
Поставленная задача была решена русским
математиком П. Л. Чебышевым. Найденный
Чебышевым полином, наименее уклоняющийся
от нуля на отрезке
.
Поставленная задача была решена русским
математиком П. Л. Чебышевым. Найденный
Чебышевым полином, наименее уклоняющийся
от нуля на отрезке ,
получил название полинома Чебышева
1-го рода.
,
получил название полинома Чебышева
1-го рода.
Полиномом
Чебышева 1-го рода степени
 называется функция вида
называется функция вида
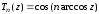 ,
,
 ,
,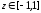 .
.
Обозначив
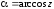 ,
получим
,
получим
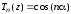 ,
,
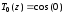 ,
,
 ,
,
 ,
,
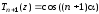 .
.
Так как по формуле суммы косинусов
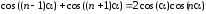 ,
,
то
справедливо соотношение
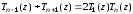 .
Отсюда получаем рекуррентную формулу
для полиномов Чебышева:
.
Отсюда получаем рекуррентную формулу
для полиномов Чебышева:
 .
(3.29)
.
(3.29)
По этой формуле, в частности, имеем:
 ,
,
 ,
,
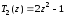 ,
,
 ,
,
 ,
,
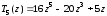 .
.
Из
рекуррентной формулы (3.29) следует, что
коэффициент при старшей степени полинома
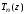 равен
равен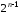 .
Нормированным полиномом Чебышева 1-го
рода степени
.
Нормированным полиномом Чебышева 1-го
рода степени называется полином
называется полином
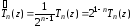 .
(3.30)
.
(3.30)
Коэффициент
при старшей степени нормированного
полинома Чебышева
 равен единице. Если
равен единице. Если ,
,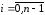 ,
– корни полинома
,
– корни полинома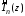 ,
то
,
то
 ,
,
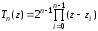 .
(3.31)
.
(3.31)
Из
определения полинома
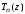 ясно, что
ясно, что .
Тогда
.
Тогда
 ,
,
 .
.
Можно
доказать, что это максимальное значение
на отрезке
 достигается, т.е.
достигается, т.е.
 .
(3.32)
.
(3.32)
Полиномы
Чебышева 1-го рода ортогональны на
отрезке
 по весу
по весу
 ,
,
т.е.

Они
также являются ортогональными на системе
точек
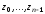 ,
т.е.
,
т.е.
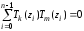 ,
,
 .
.
