5.4 Метод простой итерации

Преобразуем уравнение (5.1) следующим образом. Умножим обе части уравнения на некоторую функцию 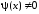. Получим эквивалентное уравнение

.

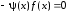Прибавив к обеим частям последнего уравнения , получим уравнение

, (5.3)

где

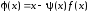. (5.4)

Организуем итерационный вычислительный процесс по формуле

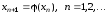, (5.5)

где 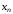– начальное значение корня уравнения,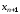– последующее уточненное значение корня. Формула (5.5) и есть алгоритм метода простой итерации.

В обозначениях исходного уравнения (5.1) алгоритм простой итерации записывается в виде

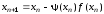. (5.6)

Выполнение расчетов по формуле (5.5) или (5.6) называется одной итерацией. Итерации прекращают, когда

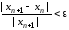, (5.7)

где число определяет допустимую относительную погрешность нахождения корня.

Исследуем сходимость метода простой итерации. Пусть 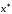– корень уравнения (5.3). В этом случае имеем равенство

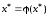. (5.8)

Вычитая из (5.5) выражение (5.8), получим

.

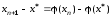Применим к правой части последнего выражения теорему Лагранжа, т.е. воспользуемся равенством

,

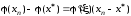где 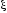лежит между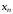и. Получим

.

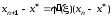Обозначим

,

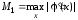где максимум берется по всем , которые могут встретиться в процессе итераций. Тогда можно записать, что

.

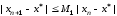Заменяя здесь на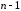, получим

.

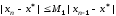Два последних неравенства позволяют записать, что

.

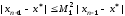Продолжая процесс уменьшения и подстановок, в конечном итоге получим

,

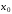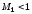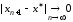где – первоначальное приближение к корню. Очевидно, что если, тои, т.е. итерации сходятся к корню уравнения (5.3). Итак, мы показали, что метод простой итерации сходится, если

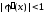(5.9)

для значений на всех итерациях.

Сходимость метода простой итерации иллюстрируется рисунком 5.4.

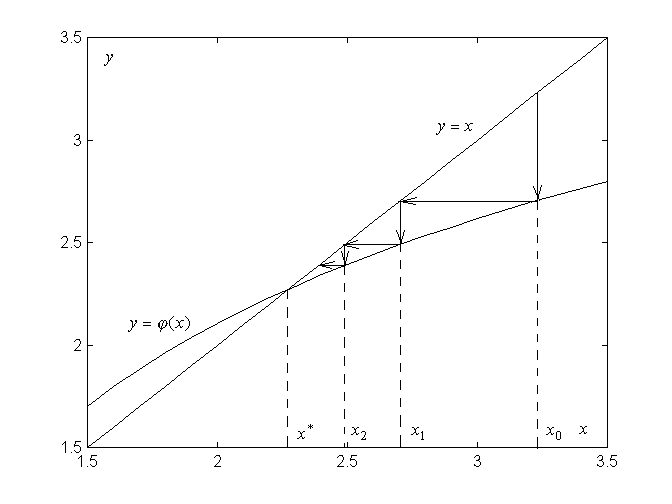
Рисунок 5.4 – Иллюстрация сходимости метода простой итерации

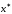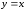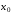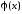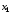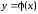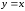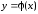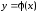Корень уравнения (5.3) определяется как точка пересечения кривойи прямой. Выбирая первоначальное приближениеи подставляя его в функцию, получаем новое приближение. Итерационный процесс изображен на рисунке 5.4 в виде прямых со стрелками. Горизонтальные прямые со стрелками соответствуют приравниванию значений функцийи, вертикальные – подстановкам значенийв функцию. Функцияв данном случае удовлетворяет условию сходимости (5.9), и от итерации к итерации получаем значения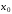,,, 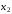…, все более близкие к корню.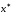

Рисунок 5.5 иллюстрирует расходимость метода простой итерации.

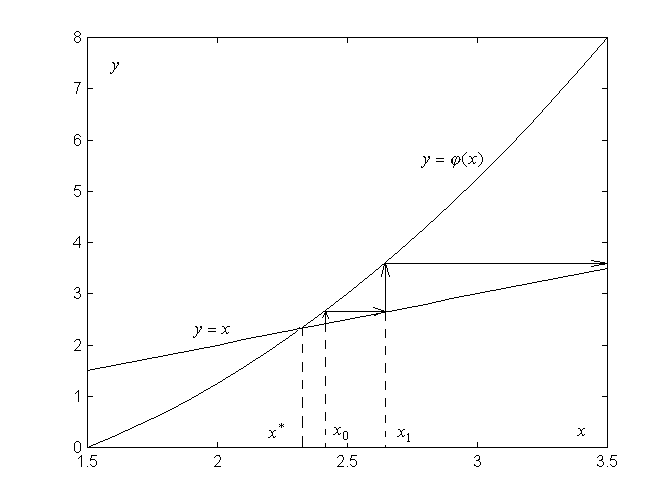
Рисунок 5.5 – Иллюстрация расходимости метода простой итерации

Функция 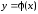в данном случае не удовлетворяет условию сходимости (5.9), ее производная по модулю больше единицы (она возрастает быстрее, чем функция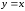). В итоге итерации расходятся.

Если решается уравнение (5.1) и оно сводится к уравнению (5.3) с помощью подстановки (5.4), то условие сходимости (5.9) принимает вид

.

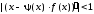Выбором функции 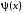в формуле для итераций (5.6) можно влиять на сходимость метода. В простейшем случае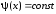со знаком плюс или минус.

Пример 5.1. Пусть требуется найти квадратный корень некоторого положительного числа , т.е. найти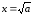. Решение этой задачи эквивалентно решению уравнения

.

Воспользуемся для решения этого уравнения методом простой итерации. В данном случае 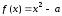,. Достаточное условие сходимости метода простой итерации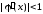приобретает вид

.

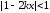Отсюда мы можем найти значение коэффициента 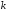, обеспечивающего сходимость метода. Получаем

, .

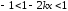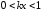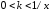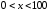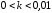Для положительных значений корня имеем. Например, дляимеем. Для нахождения корня используется следующая формула итераций:

.
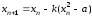