
- •Теоретический раздел Предисловие
- •Предисловие ко второму изданию
- •1 Математические модели. Численные методы. Погрешности вычислений
- •1.1 Математические модели и моделирование
- •1.2 Этапы численного решения задач на эвм
- •1.3 Виды погрешностей решения задач
- •1.4 Погрешности арифметических операций
- •1.5 Графы арифметических операций
- •1.6 Распространение погрешностей в вычислениях
- •2 Решение систем линейных алгебраических уравнений
- •2.1 Постановка задачи. Методы решения
- •2.2 Метод Гаусса
- •2.2.1 Описание метода Гаусса
- •2.2.2 Расчетные формулы метода Гаусса
- •2.2.3 Погрешность метода Гаусса. Метод Гаусса с выбором главного элемента
- •2.3 Вычислительная сложность метода Гаусса
- •2.4 Обращение матрицы
- •2.5 Метод lu-разложения
- •2.6 Метод квадратного корня решения симметричных слау
- •2.7 Метод Гаусса–Зейделя
- •2.7.1 Расчетные формулы метода Гаусса–Зейделя
- •2.7.2 Сходимость метода Гаусса–Зейделя
- •2.7.3 Графическая иллюстрация метода Гаусса–Зейделя
- •3 Аппроксимация функций
- •3.1 Понятие аппроксимации функций
- •3.2 Постановка задачи интерполирования функций
- •3.3 Интерполяционный полином Лагранжа
- •3.4 Вычисление значений полиномов
- •3.5 Вычислительная сложность задачи интерполирования
- •3.6 Конечные и разделенные разности функции
- •3.7 Интерполяционный полином Ньютона
- •3.8 Погрешность интерполирования
- •3.9 Полиномы Чебышева 1-го рода
- •3.10 Наилучший выбор узлов интерполирования
- •4 Численное интегрирование
- •4.1 Постановка задачи численного интегрирования
- •4.2 Метод прямоугольников
- •4.3 Погрешность метода прямоугольников
- •4.4 Метод трапеций
- •4.5 Погрешность метода трапеций
- •4.6 Метод Симпсона
- •4.7 Погрешность метода Симпсона
- •4.8 Интерполяционные квадратурные формулы
- •4.9 Интерполяционные квадратурные формулы наивысшей алгебраической степени точности (квадратурные формулы Гаусса)
- •4.9.1 Квадратурная формула Гаусса–Лежандра
- •4.9.2 Квадратурная формула Гаусса–Лагерра
- •4.9.3 Квадратурная формула Гаусса–Эрмита
- •5 Решение нелинейных уравнений
- •5.1 Постановка задачи численного решения нелинейных уравнений
- •5.2 Метод деления отрезка пополам
- •5.3 Метод хорд
- •5.4 Метод простой итерации
- •5.5 Метод Ньютона
- •5.6 Метод секущих
- •6 Решение обыкновенных дифференциальных уравнений
- •6.1 Постановка задачи
- •6.2 Метод рядов Тейлора
- •6.3 Метод Эйлера
- •6.4 Метод Рунге–Кутта 2-го порядка
- •6.5 Метод Рунге–Кутта 4-го порядка
- •7 Решение систем обыкновенных дифференциальных уравнений
- •7.1 Постановка задачи
- •7.2 Приведение дифференциального уравнения -го порядка к системе дифференциальных уравнений 1-го порядка
- •7.3 Метод Эйлера
- •8.2 Выполнение символьных операций в Matlab
- •8.3 Создание символьных переменных
- •8.4 Создание группы символьных переменных
- •8.5 Создание списка символьных переменных
- •8.6 Вывод символьного выражения
- •8.7 Упрощение выражений
- •8.8 Вычисление производных
- •8.9 Вычисление интегралов
- •8.10 Вычисление сумм рядов
- •8.11 Вычисление пределов
- •8.12 Разложение функции в ряд Тейлора
- •8.13 Вычисление определителя матрицы, обращение матрицы
- •9 Дополнение
- •9.1 Вычисление корней полиномов
- •9.2 Решение систем нелинейных уравнений. Метод Ньютона
- •9.3 Решение систем линейных алгебраических уравнений с трехдиагональной матрицей (метод прогонки)
- •9.4 Интерполирование функций сплайнами
- •Практический раздел Указания к выбору варианта
- •Лабораторная работа № 1. Работа в системе Matlab
- •1.1. Цель работы
- •1.2. Порядок выполнения работы
- •Лабораторная работа № 2. Решение систем линейных алгебраических уравнений
- •2.1. Цель работы
- •2.2. Теоретические положения
- •2.3. Порядок выполнения работы
- •Лабораторная работа № 3. Аппроксимация функций
- •3.1. Цель работы
- •3.2. Теоретические положения
- •3.3. Порядок выполнения работы
- •Лабораторная работа № 4. Численное интегрирование
- •4.1. Цель работы
- •4.2. Теоретические положения
- •4.3. Порядок выполнения работы
- •Лабораторная работа № 5. Решение нелинейных уравнений
- •5.1. Цель работы
- •5.2. Теоретические положения
- •5.3. Порядок выполнения работы
- •Лабораторная работа № 6. Решение обыкновенных дифференциальных уравнений
- •6.1. Цель работы
- •6.2. Теоретические положения
- •6.3. Порядок выполнения работы
- •Лабораторная работа № 7. Решение систем обыкновенных дифференциальных уравнений
- •7.1. Цель работы
- •7.2. Теоретические положения
- •7.3. Порядок выполнения работы
- •Лабораторная работа № 8. Выполнение символьных операций
- •8.1. Цель работы
- •8.2. Теоретические сведения
- •8.3. Порядок выполнения работы
- •Литература
- •Литература
2.2 Метод Гаусса
2.2.1 Описание метода Гаусса
Дадим сначала общее описание метод Гаусса для решении СЛАУ (2.2). Этот метод состоит из двух этапов, которые называются прямым и обратным ходом. В процессе прямого хода система уравнений путем исключения переменных приводится к так называемому верхнему треугольному виду. В процессе обратного хода находится решение системы.
Прямой
ход состоит
из
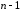 шагов
шагов .
На шаге
.
На шаге исключается неизвестная
исключается неизвестная из всех уравнений, начиная со второго.
На шаге
из всех уравнений, начиная со второго.
На шаге исключается
исключается из всех уравнений, начиная с третьего.
На любом
из всех уравнений, начиная с третьего.
На любом -м
шаге исключается
-м
шаге исключается ,
из всех уравнений, начиная
,
из всех уравнений, начиная уравнения. На последнем шаге
уравнения. На последнем шаге исключается
исключается из последнего уравнения. В результате
выполнения прямого хода мы получаем
систему уравнений с так называемой
верхней треугольной матрицей коэффициентов.
из последнего уравнения. В результате
выполнения прямого хода мы получаем
систему уравнений с так называемой
верхней треугольной матрицей коэффициентов.
Обратный
ход позволяет
последовательно получить неизвестные
системы уравнений. Сначала определяют
 из последнего
из последнего -го
уравнения. Затем это значение подставляют
в (
-го
уравнения. Затем это значение подставляют
в ( )-е
уравнение и определяют
)-е
уравнение и определяют ,
и т. д., до определения
,
и т. д., до определения из первого уравнения.
из первого уравнения.
2.2.2 Расчетные формулы метода Гаусса
Получим расчетные формулы метода Гаусса. Начнем с прямого хода. Прямой ход базируется на том, что решение системы уравнений не изменится, если из некоторого уравнения вычесть любое другое уравнение, умноженное на некоторый коэффициент. Коэффициенты подбираются таким образом, чтобы при вычитании исключались определенные переменные.
На
первом шаге для
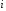 -го
уравнения начиная с
-го
уравнения начиная с вводится коэффициент
вводится коэффициент
 ,
,
и
из
 -го
уравнения вычитается 1-е уравнение,
умноженное на этот коэффициент.
Результирующее уравнение записывается
на место
-го
уравнения вычитается 1-е уравнение,
умноженное на этот коэффициент.
Результирующее уравнение записывается
на место -го.
Это приводит к исключению переменной
-го.
Это приводит к исключению переменной из
из -го
уравнения. После этого шага система
уравнений примет следующий вид:
-го
уравнения. После этого шага система
уравнений примет следующий вид:

где
 для всех
для всех – коэффициенты, полученные на первом
шаге прямого хода. Они определяются
следующими выражениями:
– коэффициенты, полученные на первом
шаге прямого хода. Они определяются
следующими выражениями:
 ,
,
 ,
,
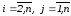 .
.
На
втором шаге для
 -го
уравнения начиная с
-го
уравнения начиная с вводится коэффициент
вводится коэффициент
 ,
,
и
из
 -го
уравнения вычитается 2-е уравнение,
умноженное на этот коэффициент. Это
приводит к исключению из
-го
уравнения вычитается 2-е уравнение,
умноженное на этот коэффициент. Это
приводит к исключению из -го
уравнения переменной
-го
уравнения переменной .
После второго шага система уравнений
примет вид
.
После второго шага система уравнений
примет вид

где
 –
коэффициенты, полученные на втором шаге
прямого хода. Они определяются выражениями
–
коэффициенты, полученные на втором шаге
прямого хода. Они определяются выражениями
 ,
,
 ,
,
 .
.
Вообще,
на
 -м
шаге для
-м
шаге для -го
уравнения начиная с
-го
уравнения начиная с вводится коэффициент
вводится коэффициент
 ,
(2.7)
,
(2.7)
и
из
 -го
уравнения вычитается
-го
уравнения вычитается -е
уравнение, умноженное на этот коэффициент.
Результирующее уравнение записывается
на место
-е
уравнение, умноженное на этот коэффициент.
Результирующее уравнение записывается
на место -го.
При этом из
-го.
При этом из -го
уравнения исключается переменная
-го
уравнения исключается переменная .
Коэффициенты системы уравнений на
.
Коэффициенты системы уравнений на -м
шаге пересчитываются по формулам
-м
шаге пересчитываются по формулам
 ,
(2.8)
,
(2.8)
 ,
(2.9)
,
(2.9)
 .
.
При
 происходит исключение
происходит исключение из последнего уравнения, и окончательная
верхняя треугольная система записывается
следующим образом:
из последнего уравнения, и окончательная
верхняя треугольная система записывается
следующим образом:
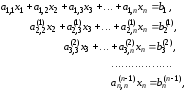 (2.10)
(2.10)
Теперь
выполняется обратный
ход. Видно,
что из последнего уравнения можно сразу
определить
 :
:
 .
.
Подставляя
это значение в предпоследнее уравнение,
находим
 :
:
 .
.
Для
нахождения любой переменной
 применяется формула
применяется формула
 .
.
Замечание.
В процессе
решения СЛАУ легко может быть получен
определитель системы
 .
Он равен произведению диагональных
элементов матрицы верхней треугольной
системы:
.
Он равен произведению диагональных
элементов матрицы верхней треугольной
системы:
 .
.
Алгоритм Гаусса реализуется по схеме, приведенной на рисунке 2.1, в том случае, когда блок № 5 «Выбор главного элемента» пропускается. Назначение этого блока описывается в п. 2.2.3.
|
|
Рисунок 2.1 – Схема алгоритма Гаусса

