6.5 Метод Рунге–Кутта 4-го порядка

Аналогично тому, как это было сделано в п. 6.4 для метода Рунге–Кутта 2-го порядка, можно вывести формулы для методов Рунге–Кутта 3-го и 4-го порядков. Без выводов приведем формулы для метода Рунге–Кутта 4-го порядка:

,

,

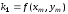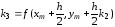, (6.18)

,

.

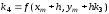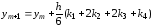Метод Рунге–Кутта 4-го порядка (6.18) имеет погрешность порядка 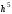. Среди методов Рунге–Кутта он наиболее употребителен.

Рассмотренные в данном разделе методы называются одношаговыми, так как для получения нового значения интегральной кривой достаточно знать лишь одно ее предыдущее значение.

7 Решение систем обыкновенных дифференциальных уравнений

7.1 Постановка задачи

Системой обыкновенных дифференциальных уравнений первого порядка называется совокупность дифференциальных уравнений следующего вида:

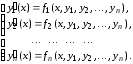(7.1)

Неизвестными здесь являются функции 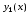,,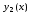 …,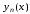независимой переменной, а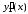,,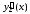 …,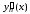– их производные. Задача Коши для данной системы дифференциальных уравнений формулируется следующим образом: найти функции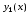,,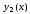 …,, удовлетворяющие равенствам (7.1) и начальным условиям

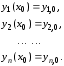(7.2)

Обычно для записи системы дифференциальных уравнений (7.1) используется векторная форма, для чего данные организуются в виде векторов. Введем в рассмотрение векторную функцию – вектор-столбец

.

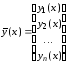Тогда можно рассматривать также вектор-столбец производной

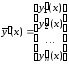
и вектор-столбец функций правой части системы (7.1)

.

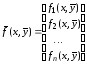С использованием этих векторных обозначений система дифференциальных уравнений (7.1) запишется в виде

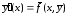, (7.3)

а начальные условия (7.2) – в виде

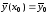, (7.4)

где

.

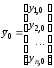Мы видим, что векторная запись (7.3), (7.4) системы дифференциальных уравнений первого порядка (7.1), (7.2) имеет тот же вид, что и дифференциальное уравнение 1-го порядка (6.1), (6.2). Это внешнее сходство позволяет предположить, что методы решения дифференциального уравнения 1-го порядка, (см. п. п. 6.3 – 6.5), можно распространить (обобщить) и на систему дифференциальных уравнений 1-го порядка вида (7.1), (7.2). Это предположение оказывается справедливым.

7.2 Приведение дифференциального уравнения -го порядка к системе дифференциальных уравнений 1-го порядка

Пусть требуется найти решение дифференциального уравнения -го порядка

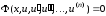, (7.5)

удовлетворяющее начальным условиям

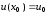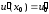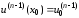, , …,, (7.6)

где 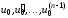– некоторые числа.

Если уравнение (7.5) можно разрешить относительно старшей производной 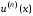, то его можно представить в виде системыдифференциальных уравнений 1-го порядка. Покажем, как это сделать. Пусть уравнение (7.5) представлено в виде

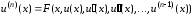. (7.7)

Для функции 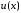и ее производных до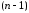-го порядка введем обозначения

,

,

,

…………….

.

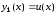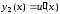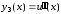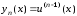Дифференцирование этих равенств с учетом выражения (7.7) дает нам следующую систему дифференциальных уравнений первого порядка:

,

,

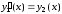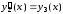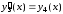, (7.8)

…………….

.

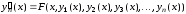Начальные условия (7.6) приобретают теперь следующий вид:

,

,

………………… (7.9)

.
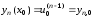