
- •Теоретический раздел Предисловие
- •Предисловие ко второму изданию
- •1 Математические модели. Численные методы. Погрешности вычислений
- •1.1 Математические модели и моделирование
- •1.2 Этапы численного решения задач на эвм
- •1.3 Виды погрешностей решения задач
- •1.4 Погрешности арифметических операций
- •1.5 Графы арифметических операций
- •1.6 Распространение погрешностей в вычислениях
- •2 Решение систем линейных алгебраических уравнений
- •2.1 Постановка задачи. Методы решения
- •2.2 Метод Гаусса
- •2.2.1 Описание метода Гаусса
- •2.2.2 Расчетные формулы метода Гаусса
- •2.2.3 Погрешность метода Гаусса. Метод Гаусса с выбором главного элемента
- •2.3 Вычислительная сложность метода Гаусса
- •2.4 Обращение матрицы
- •2.5 Метод lu-разложения
- •2.6 Метод квадратного корня решения симметричных слау
- •2.7 Метод Гаусса–Зейделя
- •2.7.1 Расчетные формулы метода Гаусса–Зейделя
- •2.7.2 Сходимость метода Гаусса–Зейделя
- •2.7.3 Графическая иллюстрация метода Гаусса–Зейделя
- •3 Аппроксимация функций
- •3.1 Понятие аппроксимации функций
- •3.2 Постановка задачи интерполирования функций
- •3.3 Интерполяционный полином Лагранжа
- •3.4 Вычисление значений полиномов
- •3.5 Вычислительная сложность задачи интерполирования
- •3.6 Конечные и разделенные разности функции
- •3.7 Интерполяционный полином Ньютона
- •3.8 Погрешность интерполирования
- •3.9 Полиномы Чебышева 1-го рода
- •3.10 Наилучший выбор узлов интерполирования
- •4 Численное интегрирование
- •4.1 Постановка задачи численного интегрирования
- •4.2 Метод прямоугольников
- •4.3 Погрешность метода прямоугольников
- •4.4 Метод трапеций
- •4.5 Погрешность метода трапеций
- •4.6 Метод Симпсона
- •4.7 Погрешность метода Симпсона
- •4.8 Интерполяционные квадратурные формулы
- •4.9 Интерполяционные квадратурные формулы наивысшей алгебраической степени точности (квадратурные формулы Гаусса)
- •4.9.1 Квадратурная формула Гаусса–Лежандра
- •4.9.2 Квадратурная формула Гаусса–Лагерра
- •4.9.3 Квадратурная формула Гаусса–Эрмита
- •5 Решение нелинейных уравнений
- •5.1 Постановка задачи численного решения нелинейных уравнений
- •5.2 Метод деления отрезка пополам
- •5.3 Метод хорд
- •5.4 Метод простой итерации
- •5.5 Метод Ньютона
- •5.6 Метод секущих
- •6 Решение обыкновенных дифференциальных уравнений
- •6.1 Постановка задачи
- •6.2 Метод рядов Тейлора
- •6.3 Метод Эйлера
- •6.4 Метод Рунге–Кутта 2-го порядка
- •6.5 Метод Рунге–Кутта 4-го порядка
- •7 Решение систем обыкновенных дифференциальных уравнений
- •7.1 Постановка задачи
- •7.2 Приведение дифференциального уравнения -го порядка к системе дифференциальных уравнений 1-го порядка
- •7.3 Метод Эйлера
- •8.2 Выполнение символьных операций в Matlab
- •8.3 Создание символьных переменных
- •8.4 Создание группы символьных переменных
- •8.5 Создание списка символьных переменных
- •8.6 Вывод символьного выражения
- •8.7 Упрощение выражений
- •8.8 Вычисление производных
- •8.9 Вычисление интегралов
- •8.10 Вычисление сумм рядов
- •8.11 Вычисление пределов
- •8.12 Разложение функции в ряд Тейлора
- •8.13 Вычисление определителя матрицы, обращение матрицы
- •9 Дополнение
- •9.1 Вычисление корней полиномов
- •9.2 Решение систем нелинейных уравнений. Метод Ньютона
- •9.3 Решение систем линейных алгебраических уравнений с трехдиагональной матрицей (метод прогонки)
- •9.4 Интерполирование функций сплайнами
- •Практический раздел Указания к выбору варианта
- •Лабораторная работа № 1. Работа в системе Matlab
- •1.1. Цель работы
- •1.2. Порядок выполнения работы
- •Лабораторная работа № 2. Решение систем линейных алгебраических уравнений
- •2.1. Цель работы
- •2.2. Теоретические положения
- •2.3. Порядок выполнения работы
- •Лабораторная работа № 3. Аппроксимация функций
- •3.1. Цель работы
- •3.2. Теоретические положения
- •3.3. Порядок выполнения работы
- •Лабораторная работа № 4. Численное интегрирование
- •4.1. Цель работы
- •4.2. Теоретические положения
- •4.3. Порядок выполнения работы
- •Лабораторная работа № 5. Решение нелинейных уравнений
- •5.1. Цель работы
- •5.2. Теоретические положения
- •5.3. Порядок выполнения работы
- •Лабораторная работа № 6. Решение обыкновенных дифференциальных уравнений
- •6.1. Цель работы
- •6.2. Теоретические положения
- •6.3. Порядок выполнения работы
- •Лабораторная работа № 7. Решение систем обыкновенных дифференциальных уравнений
- •7.1. Цель работы
- •7.2. Теоретические положения
- •7.3. Порядок выполнения работы
- •Лабораторная работа № 8. Выполнение символьных операций
- •8.1. Цель работы
- •8.2. Теоретические сведения
- •8.3. Порядок выполнения работы
- •Литература
- •Литература
9 Дополнение
9.1 Вычисление корней полиномов
Пусть
требуется найти корень полинома
 -й
степени
-й
степени
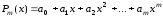 .
(9.1)
.
(9.1)
Воспользуемся методом Ньютона–Рафсона:
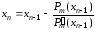 .
.
Значение
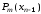 здесь можно вычислить по правилу Горнера,
т.е. с помощью соотношений
здесь можно вычислить по правилу Горнера,
т.е. с помощью соотношений
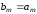 ,
,
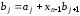 ,
,
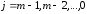 .
(9.2)
.
(9.2)
В результате получим
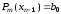 .
.
Далее, согласно (3.18) имеем
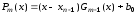 ,
(9.3)
,
(9.3)
где
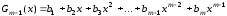 .
.
Дифференцируя (9.3), получим
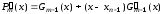 .
.
Следовательно,
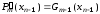 .
.
Но
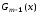 является полиномом степени
является полиномом степени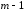 ,
так что его также можно вычислить по
правилу Горнера, воспользовавшись
рекуррентными формулами
,
так что его также можно вычислить по
правилу Горнера, воспользовавшись
рекуррентными формулами
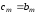 ,
,
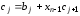 ,
,
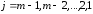 .
(9.4)
.
(9.4)
В результате получим
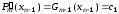 .
.
Подставляя
найденные значения
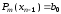 и
и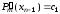 в формулу итераций Ньютона–Рафсона,
получаем, что корни полинома (9.1)
отыскиваются по итерационной формуле
в формулу итераций Ньютона–Рафсона,
получаем, что корни полинома (9.1)
отыскиваются по итерационной формуле
 .
(9.5)
.
(9.5)
Итак,
расчеты по отысканию корня полинома
выполняются в следующем порядке: по
формулам (9.2) находим
 ,
по формулам (9.4) –
,
по формулам (9.4) –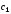 и по формуле (9.5) – новое приближение
корня. Этот метод нахождения корней
полиномов часто называют методом
Бирге–Виета.
и по формуле (9.5) – новое приближение
корня. Этот метод нахождения корней
полиномов часто называют методом
Бирге–Виета.
9.2 Решение систем нелинейных уравнений. Метод Ньютона
Система нелинейных уравнений записывается в виде
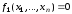 ,
,
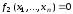 ,
(9.6)
,
(9.6)
………………….
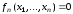 .
.
Такие
системы уравнений решаются практически
исключительно численными методами.
Изложим здесь метод Ньютона. Формулы
итераций по методу Ньютона можно получить
следующим образом. Возьмем некоторую
точку
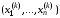 ,
которую назовем начальным приближением
к решению рассматриваемой системы
нелинейных уравнений (9.6). Разложим
функции
,
которую назовем начальным приближением
к решению рассматриваемой системы
нелинейных уравнений (9.6). Разложим
функции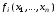 в системе (9.6) в ряд Тейлора в окрестности
точки
в системе (9.6) в ряд Тейлора в окрестности
точки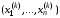 и удержим в разложении только линейные
члены. Получим следующую систему
уравнений:
и удержим в разложении только линейные
члены. Получим следующую систему
уравнений:
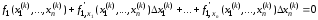 ,
,
……………………………………………………………………………….(9.7)
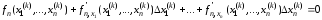 ,
,
где
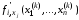 ,
,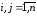 ,
– частная производная функции
,
– частная производная функции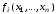 по аргументу
по аргументу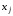 ,
вычисленная в точке
,
вычисленная в точке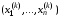 ,
и
,
и
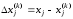 ,
,
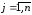 .
(9.8)
.
(9.8)
Это
– система линейных алгебраических
уравнений относительно переменных
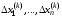 ,
которая может быть решена, например,
методом Гаусса. Получив решение этой
системы, из формулы (9.8) можем найти новое
приближение
,
которая может быть решена, например,
методом Гаусса. Получив решение этой
системы, из формулы (9.8) можем найти новое
приближение
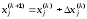 ,
,
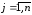 .
(9.9)
.
(9.9)
Далее
решаем систему линейных уравнений (9.7)
со значениями
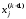 и по полученному решению находим
и по полученному решению находим
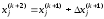 ,
,
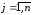 .
.
Хорошим критерием остановки процесса является условие
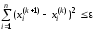 ,
(9.10)
,
(9.10)
где
 – некоторое малое число, характеризующее
допустимую погрешность вычисления
корней системы нелинейных уравнений.
– некоторое малое число, характеризующее
допустимую погрешность вычисления
корней системы нелинейных уравнений.
Более компактной является векторно-матричная форма метода Ньютона, которая позволяет также провести аналогию с методом Ньютона для решения одного уравнения. Для получения векторно-матричной формы метода Ньютона систему уравнений (9.6) записывают в векторной форме
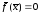 ,
,
где
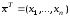 – вектор-строка неизвестных переменных,
– вектор-строка неизвестных переменных,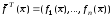 – вектор-строка функций в левой части
системы уравнений (9.6). При таких
обозначениях система линейных уравнений
(9.7) примет вид
– вектор-строка функций в левой части
системы уравнений (9.6). При таких
обозначениях система линейных уравнений
(9.7) примет вид
 ,
(9.11)
,
(9.11)
где
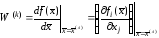 –
–
матрица
частных производных функций
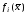 ,
вычисленная в точке
,
вычисленная в точке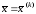 ,
,
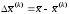 .
(9.12)
.
(9.12)
Получив
решение
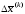 уравнения (9.11), по формуле (9.12) получим
новое приближение
уравнения (9.11), по формуле (9.12) получим
новое приближение
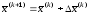 .
.
Критерий остановки процесса итераций (9.10) записывается теперь в виде
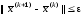 ,
,
где
 – евклидова норма вектора
– евклидова норма вектора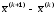 .
.
Векторно-матричная форма позволяет записать итерацию метода Ньютона в виде формулы, аналогичной формуле (5.10) метода Ньютона для одного уравнения. Действительно, уравнение (9.11) можно записать в виде
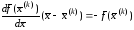 ,
(9.13)
,
(9.13)
откуда получаем следующую формулу итераций:
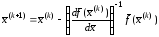 .
.
