Задача 2.3. Распределение самолетов по маршрутам

Требуется распределить самолеты трех типов по авиалиниям так, чтобы при минимальных суммарных эксплуатационных расходах перевозки по каждой из четырех авиалиний составляли не менее 300, 200, 900 и 600 ед. груза. Ниже в табл. приведены исходные данные.

Тип самолета	Число самолетов	Месячный объем перевозок одним самолетом по авиалиниям
		1	2	3	4
1	40	15	10	20	50
2	25	30	20	10	17
3	30	25	50	30	45

Тип самолета	Эксплуатационные расходы на один рейс по данному маршруту, долл.
	1	2	3	4
1	10	20	25	40
2	70	22	15	45
3	40	50	40	65

Необходимо так распределить самолеты по авиалиниям, чтобы суммарные эксплуатационные расходы были минимальными.

Решение:

Для определения того, как распределить самолеты по авиалиниям, чтобы суммарные эксплуатационные расходы были минимальными, составим матрицу исходных значений. Для этого вводим в ячейки А10:А13 значения числа самолетов, умноженное на сумму месячного объема перевозок одним самолетом, при этом значение в ячейке А13 принимаем равным 0, для того чтобы получаемая матрица стала квадратной.

В ячейки В9:Е9 заносим данные о потребностях в грузах. Диапазон ячеек В10:Е13 содержит данные, о расходах на один рейс по данному маршруту, при этом значения ячеек В13:Е13 принимаются равными 0.

Полученная таким образом матрица является матрицей исходных значений.

В данной задаче предполагается, что суммарные запасы превышают суммарные потребности (модель открыта), т.е. выполняется условие: .

Систему ограничений задачи получаем из следующих условий:

1) все грузы должны быть перевезены, т.е. , i = 1, m,

где х_ij – количество единиц груза, запланированное к перевозке от i-того поставщика к j-тому потребителю,

n – количество потребителей,

m – количество поставщиков.

2) все потребности должны быть удовлетворены, т.е. , j = 1, n.

Таким образом, экономико-математическая модель задачи имеет следующий вид:

(где с_ij·x_ij – стоимость перевозки) при ограничениях:

, i = 1, m;

, j = 1, n;

х_ij ≥ 0, i = 1, m, j = 1, n.

С учетом вышеназванных ограничений составим матрицу изменяемых значений, или матрицу перевозок. Для этого в ячейки А2:А5 записываем следующие формулы:

В ячейку А2: =СУММ(B2:F2);

В ячейку А3: =СУММ(B3:F3);

В ячейку А4: =СУММ(B4:F4);

В ячейку А5: =СУММ(B5:F5).

В ячейки В6:Е6 записываем следующие формулы:

В ячейку В6: =СУММ(B2:B6);

В ячейку С6: =СУММ(C2:C6);

В ячейку D6: =СУММ(D2:D6);

В ячейку E6: =СУММ(E2:E6).

Ячейки диапазона В2:Е5 можно оставить пустыми. В них после ввода необходимых условий и ограничений появятся искомые данные.

В ячейку В15 вводим формулу: =СУММПРОИЗВ(B10:Е13;B2:Е5).

Дополнительное условие:

Введем условие для ограниченности самолетов.

, где C_i – фактический объем перевозок на i – ой авиалинии в месяц, j – ым типом самолета; с_i – месячный объем перевозок одним самолетом; Z – количество самолетов данного типа.

Получаем:

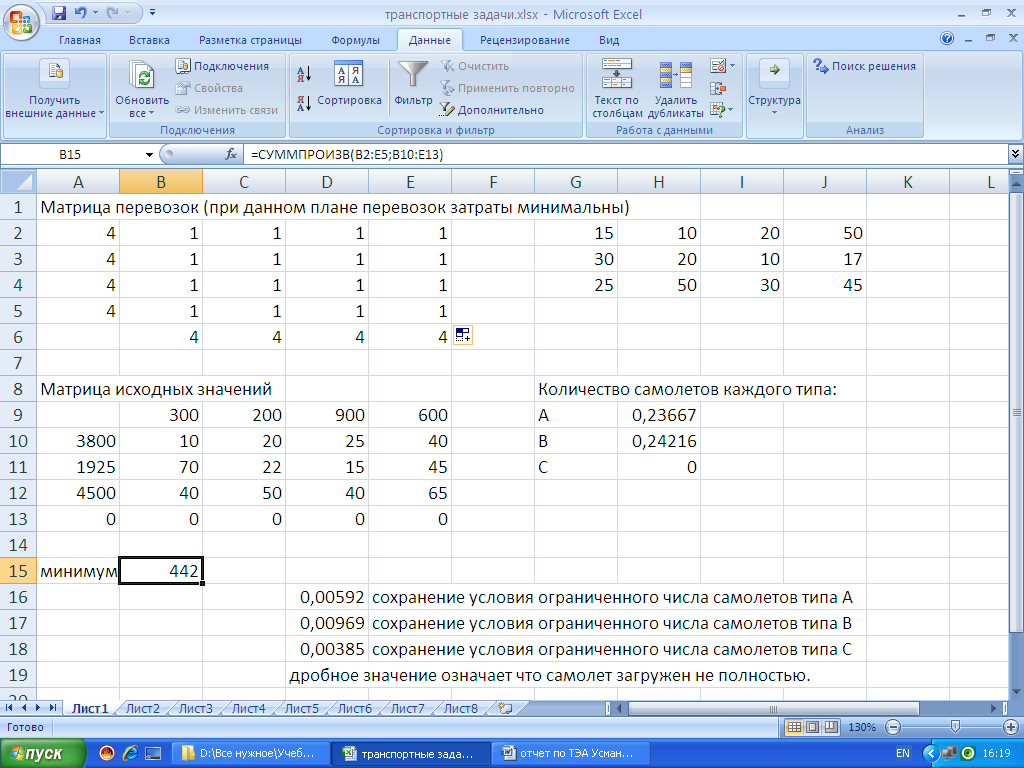
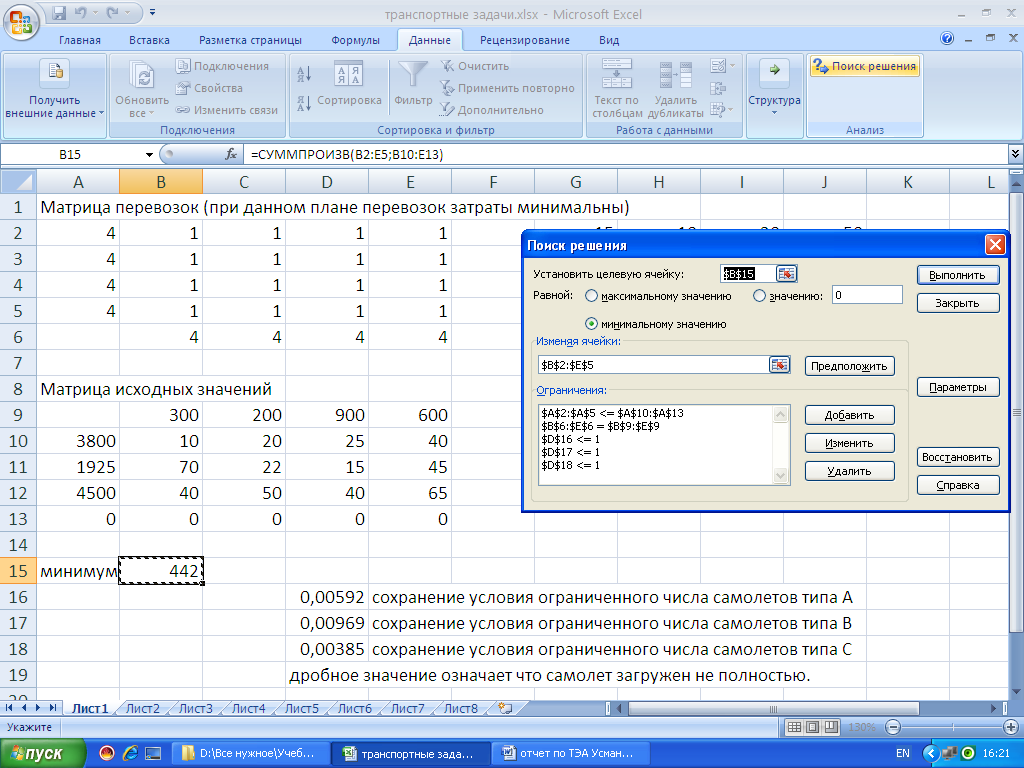
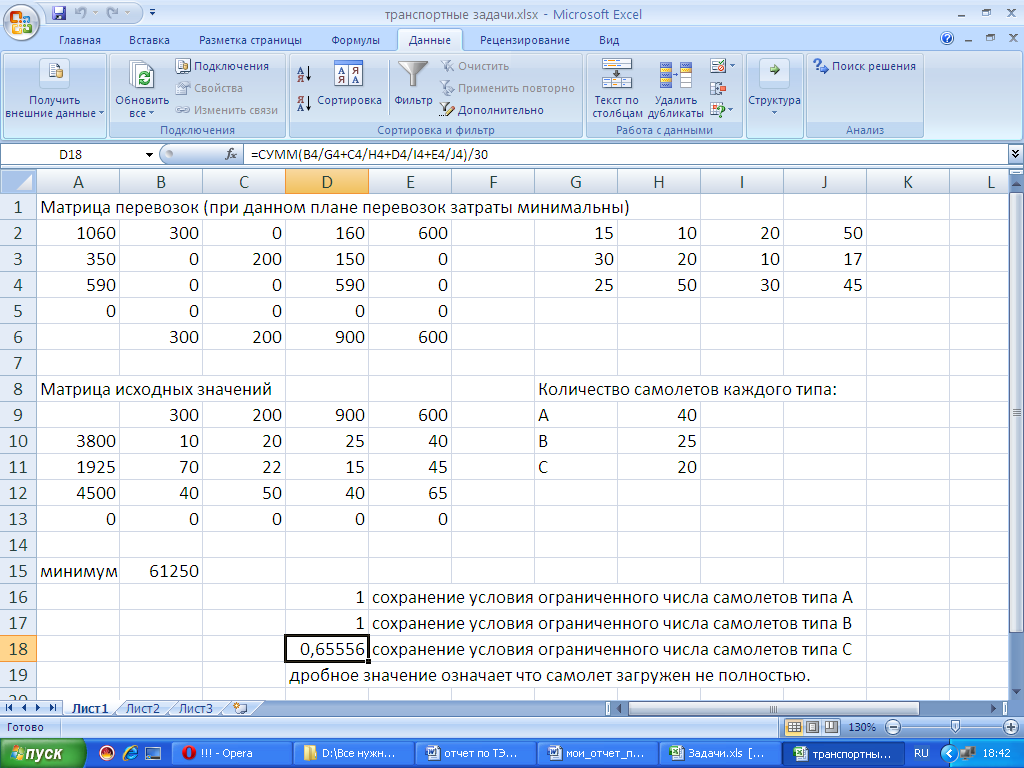
Теперь можно составить матрицу распределения самолетов данного типа по авиалиниям, где

	Оптимальное распределение самолетов
40	20	0	8	12
25	0	10	15	0
20	0	0	20	0
0	0	0	0	0
Доступное количество самолетов данного типа

Ответ:

При данных условиях минимальные эксплуатационные, суммарные расходы равны 61250 денежных единиц.